INTERNATIONAL MATHEMATICAL
OLYMPIAD 1967
The Yugoslavs were hosts to the Ninth International Mathematical
Olympiad (IMO) in which thirteen countries took part. This was held
in Cetinje, the former capital of the kingdom of Montenegro, from
3–12 July. The body responsible for the organization of the
Olympiad was the Union of the Societies of Mathematicians, Physicists
and Astronomers of Yugoslavia.
Mathematical Olympiads are mass problem-solving contests held each
year, mainly in the Socialist countries of Europe. They have been
fostered because they are regarded as of value in stimulating interest
in, and raising standards among, second school students, and in
helping to discover the highly talented.
The first IMO was held in Rumania in 1959, and up to this year
participants were always from the Socialist countries. However, the
Yugoslavs decided to invite other nations, and it was during a visit
to Austria by the former Yugoslav Master of Education that an
invitation to attend was made to Mr. A. C. Crosland,
M.P., then Secretary of State for Education and
Science. This was accepted, and the Guinness Awards, as organizers of
the National Mathematical Contest and the British Mathematical
Olympiad, was asked to be responsible for sending out the English
team. Other non-Communist countries taking part were: France, Sweden
and Italy.
The English team was made up as follows: Head of the Delegation:
Mr. R. C. Lyness, HMI; Deputy Head: Dr. N. A. Routledge, Maths. Master
at Eton College. Organizer: Mr. Maurice Goldsmith.
Professor Walter Hayman, F.R.S., who with his wife
sets and marks the questions for the British Olympiad, had a prior
engagement in Canada. They had invited the following boys, who
accepted: George Cameron-Smith, 18.0, King Edward VI School,
Stafford; Anthony Laing Davies, 17.9, Robert Hill, 18.2, Malcolm
John Williamson, 16.8, Manchester Grammar; Patrick Phair, 18.3,
Michael Cullen, 18.3, Winchester; Simon Norton, 15.4, David
Garland, 17.4, Eton.
The IME have no permanent staff, but the national host organization
is responsible for all administration from year to year. The
‘sovereign’ body is the Jury which meets before and during
the Olympiad. It is made up of the Heads and Deputies of all
participating countries, although only one vote is allowed per
country.
The Jury was comprised of the Heads of the twelve delegations, and
discussed twelve questions which had been chosen by the host country
from the bank of questions to which each country had previously
supplied six. After much discussion six were chosen and marks
assigned.
Some questions were found to be insufficiently original, some too
easy, some too difficult and some outside the knowledge conventionally
to be expected from students in all the participating countries. One
question, number 6, was originally worded in a form involving a father
leaving a hoard of gold coins to his sons in accordance with the terms
of a will and the Jury changed the setting of this problem so as to
accord better with modern socialist spirit.
The questions in the past have always included
‘planimetry’ and ‘terminals’ (traditional
trigonometrical and geometrical constructions and proofs) and have not
involved calculus, mechanics or more than easy co-ordinate geometry.
Those students who had knowledge ‘outside the questions’
could use it, of course, to solve the problems.
When the questions had been answered, each Head and Assistant
‘marked’ the papers from his own country and submitted the
marking for each question to a Yugoslavian co-ordinator who went
through the marking and approved the final mark given.
The competitors must not have reached university, and the maximum
age is 19 years 6 months. They sat for two papers on two successive
days (4 and 5 July). Each paper contained three problems, all of
which were to be done in 4 hours.
The problems presented this year were as follows:
1st Day
-
ABCD is a parallelogram. AB = a,
AD = 1, 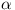 is the size of
is the size of 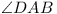 ,
and the three angles of triangle ABD are acute.
,
and the three angles of triangle ABD are acute.
Prove that the four circles KA,
KB, KC, KD, each
of radius 1, whose centres are the vertices A,
B, C, D, cover the
parallelogram if and only if 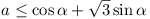
(Czechoslovakia: 6 points)
-
One side, and only one side, of a tetrahedron is of length
greater than 1. Show that its volume is equal to or less than
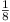 .
.
(Poland: 7 points)
-
k, m and n are
positive whole numbers, and m + k + 1 is a prime
number greater than n + 1.
Write Cs for s(s + 1).
Prove that the product
(Cm+1-Ck)(Cm+2-Ck)....(Cm+n-Ck)
is divisible by the product C1C2C3...Cn.
(England: 8 points)
2nd Day
-
The triangles A0B0C0 and
A1B1C1 have all their angles acute. Describe
how to construct one of the triangles ABC, similar
to A1B1C1 and circumscribing
A0B0C0 (so that A,
B, C correspond to
A1, B1, C1, and
AB passes through C0,
BC through A0, and
CA through B0).
Among these triangles ABC, describe, and prove,
how to construct the triangle with the maximum area.
(Italy: 6 points)
-
Consider the sequence (cn):
c1 = a1 + a2+ ... + as
c2 = a12 + a22 + ... + as2
cn = a1n + a2n + ... + asn
where a1, a2, a3,
, as are real numbers, not all
equal to zero.
Being given that, among the numbers of the sequence
(cn), there is an infinity equal to zero,
determine all the values of n for which cn
= 0.
(U.S.S.R.: 7 points)
-
In a sports meeting lasting n days there are
m medals to be won.
On the first day, one medal and 1/7 of the remaining (m
- 1) medals are won.
On the second day, 2 medals and 1/7 of the remainder are won.
And so on.
On the nth day (the last) exactly
n medals are won.
How many days did the meeting last, and what was the total
number of medals?
(Hungary: 8 points)
About half the contestants were awarded prizes. England gained one
First Prize, two Second Prizes and four Third Prizes, and our total of
marks (231), was beaten only by Russia (275), Hungary (251) and East
Germany (257), who make elaborate arrangements for preparing for the
Olympiad, with special schools, training camps, etc. A young English
contestant (from Eton College) gained one of the three
“certificates of special elegance”.
There were ninety-nine competitors, of whom only one, from
Bulgaria, was a girl.
The Yugoslav Minister of Education was present at the opening and
at the award ceremony. He expressed his pleasure at the interest in
mathematics and expressed the goodwill that arises from this
international fraternization. This was most apparent in the visits to
the beautiful coast of Jugoslavia and places in the impressive
mountains.
The 1968 IMO is to be held in Moscow.
The table below gives a consolidated score obtained by all
countries participating.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|
| Bulgaria | 7 | 14 | 24 | 20 | 20 | 11 | 21 | 42 | 159 |
| Czechoslovakia | 16 | 27 | 30 | 24 | 9 | 13 | 11 | 29 | 159 |
| East Germany | 42 | 30 | 23 | 42 | 39 | 35 | 13 | 33 | 257 |
| England | 24 | 28 | 18 | 36 | 34 | 28 | 41 | 22 | 231 |
| France1 | 4 | 10 | 9 | 6 | 12 | — | — | — | 131 |
| Hungary | 34 | 31 | 38 | 33 | 23 | 26 | 38 | 28 | 251 |
| Italy2 | 20 | 35 | 19 | 7 | 26 | 3 | — | — | 147 |
| Mongolia | 10 | 11 | 26 | 5 | 6 | 9 | 7 | 13 | 87 |
| Poland | 22 | 8 | 12 | 7 | 18 | 5 | 9 | 20 | 101 |
| Romania | 34 | 42 | 22 | 17 | 29 | 19 | 28 | 23 | 214 |
| U.S.S.R | 37 | 35 | 32 | 42 | 27 | 28 | 39 | 25 | 275 |
| Sweden | 16 | 10 | 15 | 28 | 9 | 20 | 14 | 23 | 135 |
| Jugoslavia | 13 | 18 | 11 | 18 | 26 | 22 | 6 | 22 | 136 |
Notes: 1 took part on
second day only; 2 had only six
competitors.
Report reproduced from The Science Teacher volume 11 number 1
(October 1967) pages 30 and 31.
International Mathematical Olympiad 1967
The solutions, prepared by Dr. N. A. Routledge, are as follows:
| Q1 |
Let O1 be the circumcentre of ABD,
and R the circumradius. It is clear that 3 circles
of radius R, centres A,
B and D, cover the triangle.
 If If 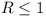 , the four circles cover the
parallelogram. , the four circles cover the
parallelogram.
Equally,
![[diagram for question 1]](1967-fig0.png)
if O2 is the circumcentre of
BCD,
it is clear that R = O2C < O1C (since
O1 and O2 are images in
BD).
 If the four circles cover the
parallelogram, they cover O1, and so one of
O1A, O1B, O1D,
O1C is If the four circles cover the
parallelogram, they cover O1, and so one of
O1A, O1B, O1D,
O1C is 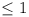 . .
 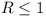 . .
Hence 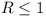 is a N.S.C. for the
parallelogram to be covered. is a N.S.C. for the
parallelogram to be covered.
Now 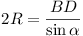 (well known) (well known)
 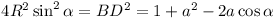
 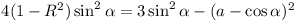
Now 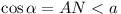
 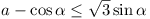 is also a N.S.C., or is also a N.S.C., or 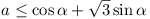 . .
|
| Q2 |
Let us assume that all sides save CD are 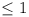 , and that CD is
unrestricted. , and that CD is
unrestricted.
![[diagram for question 2]](1967-fig1.png)
For any tetrahedron it is clear that we increase the volume if
we change CD so that  (since Vol. = (since Vol. =
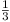 ×
ABD × height of C above
ABD). ×
ABD × height of C above
ABD).
 for any tetrahedron, for any tetrahedron, 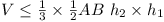 . .
Consider ABD:
![[diagram for question 2]](1967-fig2.png)
Since 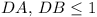 , D lies in the common region of
the two circles, radius 1, centres A and
B. Hence , D lies in the common region of
the two circles, radius 1, centres A and
B. Hence 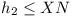 . .
Let AB = 2x. Then 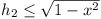 . Similarly . Similarly
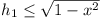 . .
 Vol. Vol. 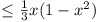 . Now if . Now if 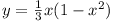 , ,
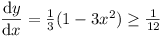 , for , for 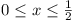 . .
 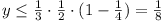
for 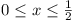 . .
 Volume Volume 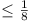 . .
|
| Q3 |
| Note that Cp - Cq | = | p(p+ 1) - q(q + 1) |
| = | p2 - q2 + p - q |
| = | (p - q)(p + q + 1) |
 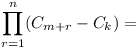
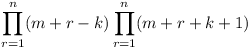
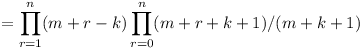 , ,
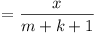 , say. , say.
Now it is well known that a sequence of n (or
n + 1) consecutive whole numbers (positive or
negative or mixed) is divisible by n! (or (n
+ 1)!) (this follows by considering binomial
coefficients).
 x is divisible
by n!(n + 1)! x is divisible
by n!(n + 1)!
But x is clearly divisible by (m + k +
1), which, being prime and > n + 1, has
no common factor with n!(n + 1)!
 x is divisible
by their product, n!(n + 1)!(m + k + 1). x is divisible
by their product, n!(n + 1)!(m + k + 1).
 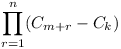 is divisible n!(n + 1)! is divisible n!(n + 1)!
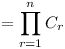 . .
|
| Q4 |
Lemma. In the figure, if AB varies so
that it
![[diagram for question 4]](1967-fig3.png)
passes through X, and A and
B are on the ‘outer’ segments of the
circles, AB is longest when it is  to XY. to XY.
For 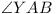 and and
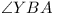 are fixed, so are fixed, so
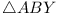 is of
fixed shape and thus it is enough to maximize
AY. is of
fixed shape and thus it is enough to maximize
AY.
For this AY is a diameter, and so 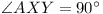 . (Note that,
if one of the ‘outer’ arcs is less than a semicircle,
this cannot be so.) . (Note that,
if one of the ‘outer’ arcs is less than a semicircle,
this cannot be so.)
For the main problem it is easy to see that A
and B (and C, in fact) lie on arcs
of circles on the sides of A0B0C0, and since
ABC is always of the same shape, to maximize its
area we need only maximize AB, and using the lemma
seems to lead directly to a solution of the problem. However, not
all points on the arc on B0C0 are possible
positions for A (in some cases) (and similarly for
B), and it is necessary to show that our
construction for a maximum triangle leads to permissible positions
for A and B.
(This is left as an exercise for the reader.)
|
| Q5 |
Since not all ai = 0, C2n >
0.
 C2n+1 = 0 for C2n+1 = 0 for
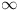 many
n. (A). many
n. (A).
If, among the ai, two are equal and opposite,
replace them both by 0. Since x2n+1 + (-x)2n+1 =
0, the property (A) still holds. Do this as often as
possible.
Finally, either (i) all ai = 0, in which case,
originally, the a were capable of being grouped
into equal and opposite pairs.
 Cn = 0 for all odd
n. Cn = 0 for all odd
n.
or (ii) some 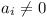 ,
but there are no equal and opposite pairs. ,
but there are no equal and opposite pairs.
Case (ii) is impossible, for if M = one of the
ai of maximum modulus, then, since
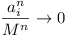 as as 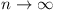
if |ai| < |M|, then 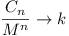 as as 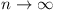 , where
k ( , where
k (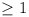 ) is
the number of ai = M. Thus ) is
the number of ai = M. Thus 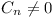 for all sufficiently
large n, conflicting with (A), which still holds for the
transformed (ai). for all sufficiently
large n, conflicting with (A), which still holds for the
transformed (ai).
|
| Q6 |
Let ar = number of medals still not awarded. at
start of rth day.
 a1 = m. a1 = m.
and 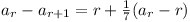 (
(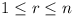 ) where
an+1 = 0. ) where
an+1 = 0.
 6ar - 7ar+1 =
6r. 6ar - 7ar+1 =
6r.
A little rough work leads us to
6(ar + 6r - 42) = 7(ar+1 + 6(r + 1) - 42)
 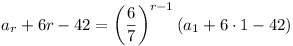
(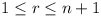 ). ).
Since a1 = m, an+1 = 0,
then
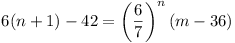
 7n(n - 6) = 6n-1 (m -
36) (i) 7n(n - 6) = 6n-1 (m -
36) (i)
 6n-1 | n - 6.
But for n = 2, ..., 5, no power of 6 divides
n - 6. 6n-1 | n - 6.
But for n = 2, ..., 5, no power of 6 divides
n - 6.
But 6n-1 > n - 1 for 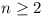 (easily proved, by
induction) (easily proved, by
induction)
 6n-1 > n - 6,
> 0 for n > 6 and so 6n-1
does not divide n - 6. 6n-1 > n - 6,
> 0 for n > 6 and so 6n-1
does not divide n - 6.
This leaves only n = 6, and so m =
36 from (i). We have shown that there can be only one
solution. But we have still to show that m = 36,
n = 6 corresponds to a realisable situation (it
might be that, although (i) is satisfied, we get fractional
numbers of medals.)
This follows from the table:
| Day | Number of
medals
awarded that day | Number of
medals then
left |
|---|
| 1 | 1+5 | 30 |
| 2 | 2+4 | 24 |
| 3 | 3+3 | 18 |
| 4 | 4+2 | 12 |
| 5 | 5+1 | 6 |
| 6 | 6 | 0 |
|
Solutions reproduced from The Science Teacher volume 11 number 4
(March 1968) pages 14 and 15.
I have been unable to locate the copyright holder of The
Science Teacher; if you believe you own the copyright, please
let me know.
Return to IMO Register home page
Contact: Joseph Myers
(imo-register@imo-register.org.uk)
Online HTML version last updated:
5 January 2016
![]() is the size of
is the size of ![]() ,
and the three angles of triangle ABD are acute.
,
and the three angles of triangle ABD are acute.![]()
![]() .
.![[diagram for question 1]](1967-fig0.png)
![[diagram for question 2]](1967-fig1.png)
![[diagram for question 2]](1967-fig2.png)
![[diagram for question 4]](1967-fig3.png)