XIth INTERNATIONAL MATHEMATICAL
OLYMPIAD, BUCHAREST, JULY 1969
A Brief Report

Fourteen countries participated. The British team of 8 boys, chosen on the results of the British Mathematical Olympiad held last May—D. J. Aldous, P. M. Bennett, A. J. Mclsaac, S. P. Norton, J. F. Segal, P. D. Smith, A. G. Trangmar, and N. S. Wedd—was placed fifth (after Hungary, E. Germany, U.S.S.R. and Romania). Mr. L. Beeson and I accompanied the team on behalf of the Association (which was asked by the Department of Education and Science to arrange British participation—and has also recently accepted responsibility for the mathematical oversight of the National Mathematical Contest and the British Mathematical Olympiad, presently administered by Guinness Awards on behalf of the organising committee).

Norton gained full marks and a First Prize, Aldous a Second Prize, Smith a Third Prize; Norton, Aldous and Wedd obtained Special Prizes awarded for elegant solutions. The questions were chosen by the International Jury (the 14 “chiefs of delegation”), and answered in two morning sessions of 4 hours each. Each leader and his colleague marked the scripts of their own team, in conjunction with the Romanian “co-ordinators”, and prizes were determined by the Jury. The boys meanwhile embarked on a fascinating, if strenuous, week-long tour of N. Romania, in the latter part of which Mr Beeson was able to join. The hospitality of our Romanian hosts was excellent, and we all greatly enjoyed the visit, forming many new friendships. Our thanks are due to the organisations and individuals who made it possible.

F. R. WATSON

Institute of Education,
University of Keele.

Paper I (4 hours)

1. Prove that there are infinitely many natural numbers a with the following property: the number z = n⁴ + a is not prime for any natural number n.

   (E. Germany, 5 marks)

2. Let a₁, a₂, ..., a_n be real constants, x a real variable and

   

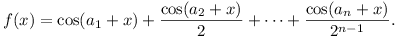
   Prove that, if f(x₁) = f(x₂) = 0, then 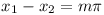, where m is an integer.

   (Hungary, 7 marks)

3. For each value of k = 1, 2, 3, 4, 5 find the necessary and sufficient conditions on the number a > 0 for there to exist a tetrahedron with k edges of length a and the remaining 6 - k edges of length 1.

   (Poland, 7 marks)

Paper II (4 hours)

4. A semi-circular arc is drawn on AB as diameter. C is a point of distinct from A and B, and D is the orthogonal projection of C on AB. We consider three circles 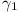, , 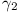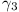which have AB as a common tangent. Of these 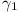is the circle which is inscribed in the triangle ABC and 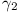, 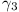are both tangential to the line-segment CD and to 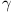. Prove that 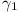, , 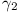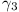have a second tangent in common.

   (Holland, 6 marks)

5. Given n > 4 points in a plane such that no three are collinear, prove that one can find at least convex quadrilaterals whose vertices are four of the given points.

   (Mongolia, 7 marks)

6. Given x₁ > 0, x₂ > 0, x₁y₁ - z₁² > 0, and x₂y₂ - z₂² > 0, prove that

   

   Give necessary and sufficient conditions for equality.

   (U.S.S.R., 8 marks)

[Mr. Watson kindly sent abbreviated solutions, but space is short and our readers enthusiastic solvers. E.A.M.]

Reproduced with permission from The Mathematical Gazette volume 53 number 386 (December 1969) pages 395–396
© 1969 Mathematical Association.

Return to IMO Register home page