International
Mathematical
Olympiad 1969
F. R. Watson and L. Beeson
The XIth International Mathematical Olympiad was held in Bucharest
in July, 1969, following acceptance of an invitation from the Romanian
Ministry of Education by the Department of Education and Science. The
travel expenses of the British party were met by the Guinness Awards,
which again managed all the arrangements.
We were the guests of the Romanian Ministry of Education which
provided accommodation, pocket money, and sightseeing trips on a very
generous scale, as will be seen from Mr. Beeson’s account.
The British team consisted of: F. R. Watson, University of Keele,
Institute of Education (Head of delegation), L. Beeson, Bishop
Otter College of Education, Chichester (Deputy Head), and a
team of eight boys selected on the basis of the 5th B.M.O. held in
May, 1969 (see Science Teacher, October, 1969):—D. J. Aldous
(Exeter School), P. M. Bennett (Royal Grammar School,
Newcastle), A. J. McIsaac (Charterhouse), S. P. Norton
(Eton College), J. F. Segal (Dulwich College),
P. D. Smith (Manchester Grammar School), A. G. Trangmar
(Dulwich College), N. S. Wedd (Kelly College,
Tavistock).
Fourteen countries took part, and Austria sent an observer. The
results by countries are given below, though it should be noted that
direct comparisons are misleading: some national teams are chosen with
great care and train seriously for the Olympiad—in one country
the eight contestants were hastily nominated by eight convenient
schools only a few days before departure. Further, familiarity with
the content of the questions varies widely from country to
country.
| Country | Total | No. in each class |
|---|
| | I | II | III |
|---|
| Belgium | 57 | — | — | — |
| Bulgaria | 189 | — | — | 3 |
| Czechoslovakia | 170 | — | — | 3 |
| E. Germany | 240 | — | 4 | 4 |
| France | 119 | — | 1 | — |
| Holland | 51 | — | — | — |
| Hungary | 247 | 1 | 4 | 2 |
| Jugoslavia | 181 | — | 2 | 2 |
| Mongolia | 120 | — | — | 1 |
| Poland | 119 | — | 1 | — |
| Romania | 219 | — | 4 | 2 |
| Sweden | 104 | — | — | — |
| U.K. | 193 | 1 | 1 | 1 |
| U.S.S.R. | 231 | 1 | 3 | 3 |
| | 3 | 20 | 21 |
The three British prizewinners were, in order, Norton, Aldous, and
Smith. In addition 13 prizes for solutions of special elegance were
awarded, and three of these went to Norton (question 2), and to Aldous
and Wedd (question 5).
The 112 candidates (7 of them girls), after a few days sightseeing
and settling down in Bucharest, sat the two 4-hour papers in the
Nicolae Balcescu High School on the mornings of July 10 and 11.
Before this, the international jury, consisting of the 14 heads of
delegations, had been engaged in selecting the questions; parallel
definitive versions were then prepared in four working languages
(English, French, German and Russian), which each head then
translated, where necessary, and typed out for his own team.
Photocopying facilities would have been very welcome here.
The Jury meetings were held at Snagov, some 30 km. north of
Bucharest, in a lakeside camp provided for young people aspiring to
represent Romania in rowing, canoeing and athletic events. This
isolation from the rest of the delegations—to ensure
secrecy—meant that we rapidly got to know one another through
working, eating and relaxing together (bathing in the lake was very
pleasant). Some of our Romanian interpreters, and some members of the
Jury, were highly multilingual, but even those of us with little
linguistic prowess soon became involved in animated, if ungrammatical,
conversation. The cordial atmosphere which resulted undoubtedly
helped us in our work and contributed greatly to the enjoyment of our
stay.
After the contest, the two leaders of each delegation marked the
papers of their own team, their work being co-ordinated by six
Romanian interpreters, assigned one to each question, to ensure
comparability of marking. (The Romanian marking of each question was
co-ordinated by the leaders from its country of origin). The final
meetings of the Jury, now in the Balcescu High School, were to
determine the standards for the award of 1st, 2nd and 3rd and special
prizes, and to discuss arrangements for the XII Olympiad to be held in
Hungary.
When these were concluded, we had one or two days free for
sightseeing in Bucharest before we were rejoined by the rest of the
delegation for the final ceremony. Here, prizes and certificates of
participation were presented by the President of the Romanian
Mathematical Society, Academician Professor G. C. Moisil, who had
earlier presided with great courtesy and perceptiveness at several of
our Jury meetings.
The Ceremony, which included an address by the Deputy Minister of
Education, was extensively reported on T.V. and radio, and in the
press, and it was apparent that the Romanians, in common with other
East European countries, regard education in mathematics as of
considerable importance.
Certainly, this Olympiad seemed to be fulfilling one of its
aims—that of stimulating interest in mathematics. The other
effects are perhaps equally important—the opportunity for pupils
and leaders to meet their counterparts in other countries, to compare
experiences, to widen their horizons, both mathematically and
personally, to visit a country with a very different social and
political system, to form friendships and exchange addresses. I feel
that our team performed very creditably—and that we are right to
regard these occasions, not too intensely, as more of a holiday than
an ordeal. The memories that remain—the pleasant relations with
leaders of other delegations, and the warm hospitality of our Romanian
hosts—a most enjoyable visit.
Mr. Beeson writes:
The team of British boys and I were met late on July 7 at Bucharest
airport by the secretary of the Mathematical Association of Romania,
together with our interpreter. From this moment on we received every
possible help from the Mathematical Association and from the Romanian
Ministry of Education, who were our joint hosts. Our
“base” in Bucharest was a students’ hostel at the
University, with a good canteen next door.
We had two or three excursions before the contest, seeing both old
and new parts of the capital and some of the country nearby. We had a
discussion partly in French, with a lady inspector of
education—we tried to explain the English system of education
and argued “State versus Public” with her and among
ourselves. We got to know some of the other 14 teams and tried to
relax before the contest paper.
The opening ceremony was impressive, with television coverage and
journalists in attendance. As soon as the papers began, the rain
started, and other delegations called it ‘English
weather’. On both days, the British team seemed well able to
sum up how well they had tackled the questions. This meant that they
were happy on the first day, and generally rather miserable on the
second. Our interpreter arranged visits to lakes near the city for
swimming, and helped to raise our spirits.
While we two leaders stayed in Bucharest to mark the contest
papers, the teams left in three heavily laden coaches for a
week’s trip round the north-east of the country. I was able,
through the kindness of our hosts, to join the boys after three days.
We were obviously taken on a most interesting and varied route, so it
is worth recording the principal places—other visitors to the
country might want to follow the same route. The buses went through
Bacau, to some spectacular country round Bicaz, visited monasteries in
Moldavia at Agapia, Sucevita, Moldovita and Voronet. We stayed near
the border with the U.S.S.R. at Suceava for two nights, saw superb
alpine pastures covered in wild flowers and snow-capped mountains. We
stayed generally in student hostels, or, as at Tirgu Mures and at
Brasov, in boarding schools.
Our party was rather more than 150 in all. Great care was taken of
this valuable group of young people—we had a doctor and nurse
travelling with us, for instance. This proved fortunate, since one of
the Swedish team had to have an operation for appendicitis. He was
left in hospital, with the Swedish interpreter staying in the town
near him. Our coach drivers were most skilled at coping with
well-engineered, but sometimes rough, roads. The insurance liability
sometimes daunted me.
Often our middle meal of the day (not served at mid-day!)
was provided in school canteens. They were a little different from
many school dinners, however, often starting with brandy and usually
having four courses! Perhaps our best day was the last of our trip,
when we were given a splendid welcome at a holiday camp for children
good at mathematics and science. We were told such camps were run for
those good at other subjects also, and that they did no work at the
camps—it was simply a reward for previous efforts. Even the
shyest of our team left with half-a-dozen addresses of Romanian
girls.
We returned to Bucharest for the closing ceremony. The Romanians
had rearranged this just to suit the British team, who had booked
their flight on the original closing day. A television interview with
Simon Norton and the other two First Prize winners was broadcast that
evening, as part of the coverage of the closing ceremony.
We all enjoyed the privilege of going. We were sorry not to be
able to communicate with all the delegations—the Mongolians, for
instance, spoke virtually nothing but their own language. We learnt
how far mathematics is international, and how sometimes very clever
boys feel depressed at their inability compared with even cleverer
boys. We were reminded that something more than mathematical ability
is needed in personal relationships. Often I, at least, found myself
thinking of the way that we in Britain might stage such an Olympiad,
and what we should want our guests to see and do. Should we lose much
mathematically if each team had to be four boys and four girls? We
should undoubtedly gain socially. Certainly, if we do ever act as
hosts, we shall find it very difficult to match the kindness and
generosity of our Romanian friends.
Questions
Paper I (4 hours)
-
Prove that there are infinitely many natural numbers a
with the following property: the number z =
n4 + a is not prime for any natural
number n.
(E. Germany, 5 marks)
-
Let a1, a2, ...
an be real constants, x a real
variable and
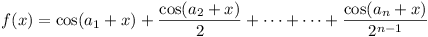
Prove that, if f(x1) = f(x2) = 0, then 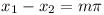 , where
m is an integer.
, where
m is an integer.
(Hungary, 7 marks)
-
For each value of k = 1, 2, 3, 4, 5 find the necessary
and sufficient conditions on the number a > 0 for there
to exist a tetrahedron with k edges of length a and
the remaining 6 - k edges of length 1.
(Poland, 7 marks)
Paper II (4 hours)
-
A semi-circular arc  is drawn on AB as diameter. C is a
point of
is drawn on AB as diameter. C is a
point of  distinct from
A and B, and D is the
orthogonal projection of C on AB.
We consider three circles
distinct from
A and B, and D is the
orthogonal projection of C on AB.
We consider three circles 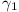 ,
, 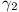 ,
, 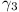 which have AB
as a common tangent. Of these
which have AB
as a common tangent. Of these 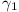 is the
circle which is inscribed in the triangle ABC and
is the
circle which is inscribed in the triangle ABC and
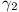 ,
, 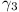 are
both tangential to the line-segment CD and to
are
both tangential to the line-segment CD and to
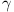 . Prove that
. Prove that 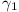 ,
, 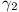 ,
, 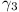 have a second tangent in common.
have a second tangent in common.
(Holland, 6 marks)
-
Given n > 4 points in a plane such that no three are
collinear, prove that one can find at least 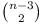 convex quadrilaterals whose
vertices are four of the given points.
convex quadrilaterals whose
vertices are four of the given points.
(Mongolia, 7 marks)
-
Given x1 > 0, x2 > 0,
x1y1 -
z12 > 0, and
x2y2 -
z22 > 0, prove that:
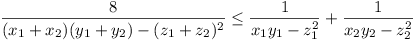
Give necessary and sufficient conditions for equality.
(U.S.S.R., 8 marks)
Solutions
-
z = n4 + a may be considered as the difference
of two squares by writing 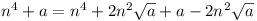
Then 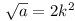 , i.e. a =
4k4 gives
, i.e. a =
4k4 gives 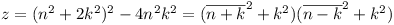 . For k > 1 each factor exceeds
1, so z is not prime. Thus if a is
of the form 4k4, z is not prime for
any n. Evidently there are an infinity of such
a.
. For k > 1 each factor exceeds
1, so z is not prime. Thus if a is
of the form 4k4, z is not prime for
any n. Evidently there are an infinity of such
a.
-
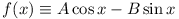 where
where 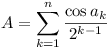 ,
,
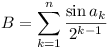
| f(x1) = f(x2) = 0 gives |
{ |
A cos x1 - B sin x1 = 0 |
| A cos x2 - B sin x2 = 0 |
If one of A, B is non-zero, it
follows that sin(x2 - x1) = 0 and 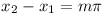 , m
integer.
, m
integer.
Thus we must show that A, B are
not both zero. Suppose the contrary.
Then 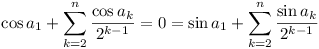 whence
whence 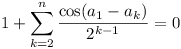 . But
. But 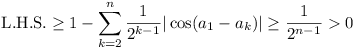 contradiction.
contradiction.
-
![[Diagram for Question 3]](1969-fig0.png)
By writing 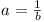 we can reduce the cases k = 4, 5 to
the cases k = 2, 1. Thus we need only consider
k = 1, 2, 3.
we can reduce the cases k = 4, 5 to
the cases k = 2, 1. Thus we need only consider
k = 1, 2, 3.
For k = 4 we have 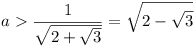 , and for k
= 5,
, and for k
= 5, 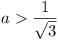 .
.
-
![[Diagram for Question 4]](1969-fig1.png)
Let the centres be Mi, their projections on
AB, Ni, the radii
ri, i = 1, 2, 3.
Let AD = p, DB = q.
We require to show that M1 M2 M3 are
collinear.
In  O M2 N2,
(½c - r2)2 = r22 + (q + r2 -
½c)2
O M2 N2,
(½c - r2)2 = r22 + (q + r2 -
½c)2
(r2 + q)2 = qc = a2.
i.e. r2 + q = a Similarly
r3 + p = b
BN1 = s - b. N1 N3 = s - b - q + r3 = s
- c and so N1 N3 = N1 N3 by
symmetry.
Thus we must prove 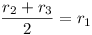 .
.
But 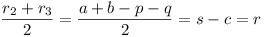 , since
, since 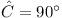
Hence M1 is the mid-point of M2
M3 and the three circles have a second common tangent
-
We can choose 3 of the points A,
B, C so that all remaining points
lie within the angle 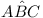 . Let X,
Y be any other point distinct from
A, B, C.
. Let X,
Y be any other point distinct from
A, B, C.
| Then if XY meets |
{ | BC |
} |
externally, |
| CA |
| AB |
| the quadrilateral |
{ | XYBC |
} |
is convex and at least one |
| XYCA |
| XYAB |
of these must hold. Thus there are at least as many convex
quadrilaterals as pairs X,
Y—i.e. at least
n-3C2.
Note: 8 students, 2 of them British, proved a much
stronger result, replacing n-3C2 by 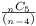 .
.
The following is the proof given by N. S. Wedd.
(i) Any set of 5 points contains at least one c.q.
(ii) There are nC5 sets of 5 points, each
containing at least one c.q.—though some sets may
have c.q.’s in common with other sets of 5.
(iii) Each c.q. can belong to at most (n -
4) such sets of 5 i.e. can be counted at most
(n - 4) times.
Hence there are at least 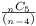 c.q. [which he then proves
c.q. [which he then proves 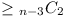 for
for 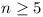 ].
].
-
Only 7 correct solutions were received for this difficult
problem; one of these, due to S. P. Norton, is given
here:—
xi > 0, 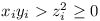
 yi > 0 and
yi > 0 and
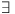 ki,
wi
ki,
wi
| such that |
xi = wiki |
} |
wi, ki > 0. |
| yi = wi/ki |
We require to prove:
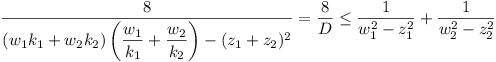 for wi > 0, wi2 >
zi2, k1 > 0, (and so wi >
/zi).
for wi > 0, wi2 >
zi2, k1 > 0, (and so wi >
/zi).
Now 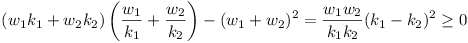 with equality iff k1 = k2
with equality iff k1 = k2
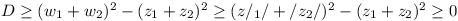 .
.
and so 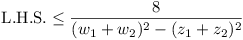 which must now be proved
which must now be proved
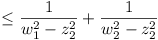
Now ai > 0, bi > 0 gives
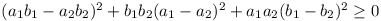 with equality iff
a1 = a2, b1 = b2.
with equality iff
a1 = a2, b1 = b2.
i.e. 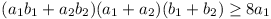 , a2 b1
b2
, a2 b1
b2
whence 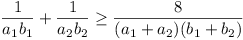
Writing wi + zi = ai, wi - zi =
bi we have the desired result
| For equality we must have | k1 = k2, | a1 = a2, | b1 = b2 |
| i.e. | k1 = k2, | w1 = w2, | z1 = z2 |
| i.e. | x1 = x2, | y1 = y2, | z1 = z2 |
| and these are clearly sufficient. |
Notes on the Questions
The students produced solutions of considerable variety. There was
admiration for the way our team used calculus or complex variable
methods in Q2, for example, and there were interesting solutions of Q6
using the minimum of the quadratic form P1(t) = x1t2 + 2z1t
+ y1.
Q6 was found hard by everyone (though 3 Hungarians produced correct
solutions), and Q4 (our worst question) was also answered badly. Q2,
3 and 5 were generally found easier; we did particularly well on
Q3.
It was evident from the results that the questions conformed more
closely to the syllabuses taught in some countries than in others (the
Swedes, for example, could attempt Q4 only by co-ordinate methods);
this factor, and the careful selection and preparation of
I.M.O. entrants which are traditional in some East European countries,
make comparisons between countries rather suspect.
However, it should be stated that the choice of questions, within
the overall broad framework, was determined by a majority vote of the
International Jury. It is necessary, too, to exclude considerable
areas of our customary Sixth Form work, since, for example, analysis
and mechanics are not commonly taught in European schools.
There seemed to be some support among members of the Jury for
questions—such as Q5—involving
“perspicacité” rather than background knowledge,
and perhaps some increase in the proportion of these would be
helpful.
Report reproduced from New Science Teacher volume 13 number 2
(December 1969) pages 59–63.
I have been unable to locate the copyright holder of New
Science Teacher; if you believe you own the copyright, please
let me know.
Return to IMO Register home page
Contact: Joseph Myers
(imo-register@imo-register.org.uk)
Online HTML version last updated:
5 January 2016
![]()
![]() , where
m is an integer.
, where
m is an integer.![[Diagram for Question 3]](1969-fig0.png)
![[Diagram for Question 4]](1969-fig1.png)
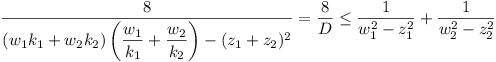 for wi > 0, wi2 >
zi2, k1 > 0, (and so wi >
/zi).
for wi > 0, wi2 >
zi2, k1 > 0, (and so wi >
/zi).