15th International Mathematical Olympiad
MOSCOW, JULY 1973—A Personal Report by F. J. Budden
| Leader: |
| F. J. Budden | Royal G.S., Newcastle upon Tyne |
| Deputy Leader: |
| R. W. Payne | Dulwich College, London |
| Team: |
| David Pritchard | Queen Mary’s G.S., Walsall |
| David Goto | St. Paul’s School, London |
| Guy Herzmark | Highgate School, London |
| Michael Beasley | Kingston G.S., Surrey |
| Malcolm Sparrow | Millfield, Somerset |
| Anthony Scholl | Worth School, Sussex |
| Richard Treitel | Eton College |
| John Hurley | Ernest Bailey G.S., Derbyshire |
A few weeks before the start of the Olympiad I was asked to act as
leader of the British delegation in place of Mr. R. C. Lyness, who had
had to withdraw for medical reasons. I had the benefit of knowing the
ropes, having been with the 13th IMO in Czechoslovakia in 1971. But
the advantages of familiarity with the procedures in preparation and
organisation, and of personal acquaintance with many of the delegates
from other countries were somewhat offset by the fact that I was
suddenly precipitated into the battle with little opportunity of
preparation for it.
Moreover, for various reasons it was found necessary for the leader
to travel in the same flight to Moscow as the team and deputy leader.
This meant that I was unable to participate in the extremely important
work of selection of questions. The 15 leaders of the remaining
countries, forming the IMO “jury” had deliberated
continuously over a period of two days, Friday and Saturday, 6 and 7
July, and by the time the British team arrived, the final selection of
six questions had been settled. Whether the British leader’s
presence at these meetings would have influenced the choice of
questions will never be known. Certainly he would have had much to
say, and meetings would have gone on longer!
The participating countries were:
| A | Austria | H | Hungary |
| BG | Bulgaria | M | Mongolia |
| CU | Cuba | NL | Holland |
| CS | Czechoslovakia | PL | Poland |
| D | Germany (E) | R | Rumania |
| FL | Finland | S | Sweden |
| F | France | SU | Soviet Union |
| GB | Great Britain | YU | Yugoslavia |
Although I thought I “knew the ropes”, there were
several departures from the procedure of two years previously in CS.
Then the students had been accommodated in hostels entirely separately
from the adults, and so had been subject to only a minimum of adult
supervision (a fact which had troubled more than one delegate,
including myself). In Moscow the arrangements were different, for
each of the deputy leaders lived in the same hotel as the students.
This not only ensured proper supervision, but it also meant that the
members of the team were able to feel in continuous contact with their
leaders instead of this contact being intermittent, and the British
deputy leader quickly established a firm rapport with the team which
contributed greatly to their morale.
The most notable contrast between 1971 and 1973 was the consequence
of the IMO being held in a capital city. In Zilina, 1971, the whole
competition was compact and intimate—persons and places were
always within easy reach. In Moscow, by contrast, the family feeling
was largely lost because personnel were so widely dispersed: students
and deputies in the University Hotel, leaders in the Ukraine Hotel
some five miles nearer the heart of the metropolis; while the rather
ordinary school in which the Olympiad was held was itself several
miles from each of these hotels.
These long lines of communication meant that one was continuously
dependent upon private transport—buses and cars laid on by the
organisers, or else upon the public buses or underground trains.
Moreover, within the mammoth Ukraine Hotel the leaders were widely
dispersed throughout the building. The British delegate in room 1707
(the hotel has 29 floors) would visit other delegates in remote rooms,
and on one occasion a visit to room 776 to collect a batch of papers
and straight back to 1707 took no less than 22 minutes, most of this
time being spent waiting for lifts (the sole means of vertical
translation). So large was the restaurant, so long were the hours
during which a particular meal was available, and so great was the
time spent waiting to be served, that it was unlikely one would meet
one’s colleagues at a meal except by assignation; the result was
less opportunity for fraternisation than had been the case in CS.
Again, in the provincial town of Zilina, the IMO had been a major
event, marked with TV coverage, a special postal franking stamp, and
flags flying. In Moscow, the event was submerged, and seemed to
receive little mention, especially as the Moscow Film Festival was in
prospect! There was less ceremonial occasions (dinners, parties), and
less organised trips (in CS we were within easy reach of country of
great scenic beauty). On the other hand, the actual business of the
competition seemed to be got through with much more despatch, and
never did meetings go on till the late hours as had occurred two or
three times in CS. A strong factor here was that, whereas in CS
proceedings had been translated in Russian, English, German, and
sometimes French, as well as Czechoslovakian, here in Moscow only
English and Russian seemed to be considered necessary. Indeed, in
general conversation it was gratifying to note that English seemed to
be the most favoured “master-language” with which almost
all delegates were familiar, to varying degrees. It was rather
surprising to find that in Moscow no attempt was made to mobilise any
photocopying apparatus, which could have greatly reduced the amount of
manual work in the preparation of the question papers and in the
dissemination of results and marks.
On 7 July, the British party arrived one hour late at Moscow
airport owing to an industrial dispute at Heathrow. This delay had
the happy result of causing us to miss the experience of flying
through a violent electric storm which had occurred at Moscow at the
scheduled arrival time. Customs and passports were formalities, only
straightforward questions being asked, and it was not long before the
parties were on the way to their hotels, having been met by Russian
IMO representatives at the airport.
I had a few hours in which to acquaint myself with the six selected
questions ready for a meeting on Sunday morning, the purpose of which
was to agree on the formulation of the questions in their final terms.
After much discussion, master versions were produced in Russian and
English, and these were precisely translated by leaders into their own
respective languages.
For various reasons, not perhaps unconnected with the speed of
meals service, the buses carrying the 125 participants together with
the deputies did not arrive until half an hour later than the
scheduled commencement of the opening ceremony. This was presided
over by Professor Markuschevich and was quite brief. The teams soon
found themselves being marshalled into eight ordinary classrooms, no
classroom containing two from the same country. The papers were
distributed, and candidates had a brief opportunity to ask for
clarification, as a result of which some minor misprints came to
light. The four-hour session lasted till almost 2.30 p.m., after
which they all had to be fed. Because of this there was some delay in
the boat trip along the River Moscow, which had been arranged for the
combined parties.
That evening the leaders with their deputies were able to begin the
marking of the papers. So far as a marking scheme was concerned, all
that had been arranged at the morning’s meeting was that the
points for the six questions should be 6+6+8+6+6+8 = 40. Subdivision
of marks within questions was left to the discretion of individual
teams, as it was thought that any discrepancies between teams could be
ironed out during the process of co-ordination which followed.
Marking of paper I continued the next morning, while the teams were
writing paper II. It may be interesting to record that the whole
process of marking plus co-ordination occupied the British leaders a
total of 22 hours. This might well have been kept below 20 hours, if
only the authorities had insisted on candidates using one side of the
paper!
Co-ordination of the questions was carried out by a team of Russian
university mathematicians. Two or three would be assigned to each of
the six questions, and they would scrutinise the answers of their
particular question for each of the 125 candidates, with the
assistance of interpreters where necessary. The object was, of
course, to secure uniformity of marking. In this difficult task, the
co-ordinators deserve the highest praise for their penetrating grasp
of the complex arguments in many languages, for their perception in
detecting subtle flaws, and for their patient determination to see
fair play.
By the morning of Thursday, 12 July, complete results of some
countries were beginning to emerge, but the full set of results were
not known till the beginning of the final meeting on Friday. In the
13th IMO, national aggregates had been computed, displayed and
discussed, whereas it was noteworthy on the present occasion that this
“team” aspect was played down, so that the truly
individual nature of the Olympiad was properly recognised.
The chief business of the meeting on Friday morning was to decide
upon the award of prizes, the main decision being to fix the
boundaries of the first, second and third class prizes. This proved
to be fairly straightforward, and the final decision was as
follows:
| 35-40 | First prizes | ( 5 entrants) |
| 27-34 | Second prizes | (13 entrants) |
| 17-26 | Third prizes | (47 entrants) |
Evidently, it was determined that golds and silvers should not be
obtained too cheaply.
Goto (who came in the GB team at the last minute as first reserve)
distinguished himself with a first prize (35 points), obtaining fifth
place in the competition; Beasley (25) narrowly missed a second prize,
and was closely followed by Treitel (22) and Herzmark (21). Pritchard
(19) and Scholl (18) were also awarded third prizes.
A happy result of the demarcation of the marks for prizes was that
Cuba received its first prize ever. Prompt action by the Cuban
leader, via the Cuban Embassy, resulted in front page treatment in the
Cuban newspapers the following day, where their successful candidate
was given a status little short of that of a national hero.
The performance by the British team may be accounted very
satisfactory: their most praiseworthy effort was in the way they
responded to Q.6, with a total of 25 points for that question from the
whole team. This was second only to USSR (30); the next best was
France with 16. Had aggregates been computed, GB would have been
placed fifth in the league. Another observation of interest is the
remarkable recovery of France, hitherto always near the bottom of the
international table, now advanced to sixth place; this was more
remarkable since their team was apparently selected from schools
confined to the Paris area.
A sprinkling of prizes for solutions of special merit had been
awarded in the past. Co-ordinators had noted specially meritorious
solutions during their work, and GB had proposed three: Herzmark for
his solution of Q.1, Beasley for Q.3, and Pritchard for Q.5.
(These we plan to publish in the next issue of
“Science Teacher”, February 1974.) It was
considered that to qualify for a special prize, most, if not all, of
the following requirements should be fulfilled: the solution should be
elegant, original (unique), flawless, brief, and the result of the
question should, if possible, be generalised by the candidate.
Unfortunately, two or three solvers had shared Herzmark’s
solution for Q.1, so this was disqualified under the first criterion;
Beasley’s for Q.3 was much liked by members of the jury, but it
had to be withdrawn under the third criterion, since Beasley had
omitted to distinguish maximum from minimum. In the end, no special
prizes were awarded to any candidate. Possibly, the restrictions were
too severe.
On 14 July, all participant teams went for an excursion, the first
occasion on which they had been taken outside the Moscow perimeter.
The closing ceremony was in the morning of Sunday, 15 July. Besides
the presentation of the 65 prizes, there were speeches of
congratulation and valediction, and the proceedings finished with a
speech by Professor Bausch of East Germany, in which he invited
representatives of the nations to compete in the 16th IMO which was to
be held in Erfurt in DDR in 1974. Meanwhile, each delegation had been
issued with a preliminary outline of the 1974 programme, from which it
was clear that this particular IMO would be very well organised. It
is understood unofficially that it is likely that the USA may be
participating for the first time.
Later that day, David Goto was interviewed through an interpreter
on Russian TV. Unfortunately, the festivities described below
prevented the transmission being seen by the rest of the company.
The final event was a dinner for all in the University Hotel. At
least, it started by being a dinner, but seemingly inexhaustible
supplies of champagne and vodka ensured the speedy evaporation of
decorum; the top table was regaled by successive teams displaying
their vocal talents in impromptu contributions; music and dancing,
including a not-to-be-forgotten performance of “Black
Eyes” by one of the co-ordinators, and other convivial
proceedings continued until the early hours.
Throughout the period of the Olympiad, there was a great deal of
fraternisation between the students of the various teams. Several
members of the British team organised an international bridge
competition; addresses, souvenirs and invitations were exchanged, and
it appeared that the IMO succeeded socially, as well as in its primary
purpose. The British leaders found the society of their colleagues
most agreeable. From many of them they received gifts, and these they
were in the happy position of being able to reciprocate thanks to
financial support by the British Awards Committee. Gifts were also
presented to some of the Russians whose courtesy, hospitality and
charm contributed so much to the success of the occasion.
Total Points by Country (maximum 320)
| SU | 256 | RU | 141 |
| H | 215 | YU | 137 |
| DDR | 189 | BG | 100 |
| PL | 174 | S | 99 |
| GB | 164 | NL | 96 |
| F | 153 | FL | 86 |
| CS | 149 | M | 64 |
| A | 147 | *CU | 42 |
*(5 entrants only)
The Questions
-
O is a point lying in a straight line
l. OP1, OP2, ...,
OPn are unit vectors with all Pi
lying in a plane containing the line l and all of
them on the same side of l. Prove that, if
n is odd, then 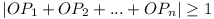 where |OM|
denotes the length of the vector OM.
where |OM|
denotes the length of the vector OM.
(CS)
-
Find out whether or not there exists a finite set
M of non-coplanar points in three-dimensional space
such that, for any two points 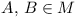 there exist two other
points
there exist two other
points 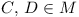 such that the straight lines AB and
CD are parallel and do not coincide.
such that the straight lines AB and
CD are parallel and do not coincide.
(PL)
-
Find the minimal value of a2 + b2, where
a and b are real numbers such that
the equation x4 + ax3 + bx2 + ax + 1 = 0 has at
least one real root.
(S)
-
A soldier has to check whether there are any mines in a region
shaped like an equilateral triangle, including its boundary. The
range of his detector is one half the altitude of the triangle.
Starting from one vertex, which path should he choose to minimise
the distance he walks to check the entire region?
(YU)
-
A non-empty set G of non-constant functions
f of the form f(x) = ax + b, where
a, b real, with 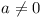 , and x
real, has the following properties:
, and x
real, has the following properties:
- If
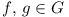 , then
, then 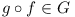 (where
(where 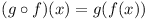 ), i.e. the set is closed under function
composition.
), i.e. the set is closed under function
composition.
- If
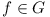 , then the
inverse function,
, then the
inverse function, 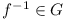 where f-1(x) = (x-b)/a for
f(x) = ax + b.
where f-1(x) = (x-b)/a for
f(x) = ax + b.
- For each
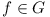 there exists an
there exists an 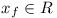 such that
f(xf) = xf.
such that
f(xf) = xf.
Prove that there exists a real number k such
that f(k) = k for all 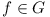 .
.
(PL)
-
Let a1, ..., an be
n given positive numbers, and let q
be a fixed real number, such that 0 < q < 1.
Find n real numbers b1,
b2, ..., bn such that
- ak < bk for all k from
1 to n.
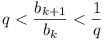 for all k from 1 to
n - 1.
for all k from 1 to
n - 1.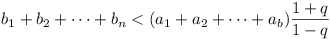
(S)
Report reproduced from Science Teacher volume 17 number 2 (December
1973) pages 8, 10 and 11.
15th International
Mathematical Olympiad
-
(Based on solution by G. Herzmark)
Suppose OPm+1 is the middle of the 2m
+ 1 vectors, and makes angle 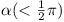 with
OX. Then we have OPr (r =
1, 2, ..., m) within angle
XOPm+1 and OPs (s = m +
2, m + 3, ..., 2m + 1)
within the obtuse angle YOPm+1. Let
with
OX. Then we have OPr (r =
1, 2, ..., m) within angle
XOPm+1 and OPs (s = m +
2, m + 3, ..., 2m + 1)
within the obtuse angle YOPm+1. Let 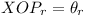 ,
, 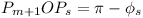 .
.
Resolute of resultant in direction 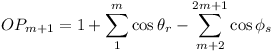 .
.
But 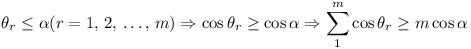 .
.
And 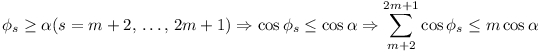 .
.
Hence the resolute along 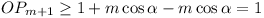 .
.
Finally the resultant, being greater than its resolute, must
also 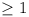 , equality
occurring only when
, equality
occurring only when 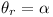 (r = 1, 2, ..., m)
and
(r = 1, 2, ..., m)
and 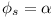 (m + 2, ..., 2m + 1).
(m + 2, ..., 2m + 1).
![[diagram for question 1]](1973-fig0.png)
-
The British team produced five complete solutions, all correct
and all essentially different. One general solution is a 3-D
lattice of points forming a block a units ×
b units × c units (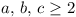 ), containing (a + 1)(b + 1)(c + 1)
points, and this requires that a, b,
c have an H.C.F. > 1. The simplest solution
(a = b = c = 2 with 27 points) was widely found,
some solvers noticing that the middle point may be omitted giving
26 points. In the general case, all the internal points
may be omitted so that only the
), containing (a + 1)(b + 1)(c + 1)
points, and this requires that a, b,
c have an H.C.F. > 1. The simplest solution
(a = b = c = 2 with 27 points) was widely found,
some solvers noticing that the middle point may be omitted giving
26 points. In the general case, all the internal points
may be omitted so that only the 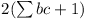 points on the surface
need to be taken.
points on the surface
need to be taken.
But not a single one of the 125 candidates found the solution
using the minimum number of points (10). This is a cube, two
opposite faces of which are surmounted by congruent right
pyramids; and any affine transformations of the above will do
equally well.
-
(Based on solution by M. Beasley)
x4 + ax3 + bx2 + ax + 1 = 0. (i) Replace
x, a, b by
t, x, y giving
t4 + xt3 + yt2 + xt + 1 = 0. (ii) which may be
re-written x(t3 + t) + yt2 + (t4 + 1) = 0, and
this represents a family of straight lines with real parameter
t. It is required to minimise x2 + y2 =
r2, i.e. the square of the distance from the origin to
any of the lines. Now the minimum distance from 0
to lx + my + n = 0 is given by
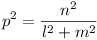
so in our case, we have
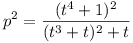
Beasley proceeded by differentiation, but the work can be
greatly reduced by using k = t2 + t-2, where
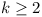 for real
t, and
for real
t, and
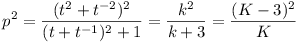
where K = k + 3, and 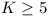 .
.
So p2 = K + 9/K - 6, and since K +
9/K is minimum when K = 3 and increases for
K > 3, the minimum p occurs when
K = 5, when p takes the value
4/5.
-
This proved to be the easiest Q. overall, but many points were
lost because solvers having found the correct minimal route,
failed to check for complete coverage.
Circular arcs are shown having radii equal to the range of the
detector (= ½h). Having reached
P on the boundary of circle centre
C, he must then proceed directly towards
B.
Total path AP + PB must be minimised. This is
achieved by having P on the altitude from
C. (Proof by reflection, confocal ellipses, etc.)
Checking for complete coverage is comparatively simple but must be
carried out exhaustively.
![[diagram for question 4]](1973-fig1.png)
-
(Solution by D. Pritchard)
Consider any two arbitrary functions from G:
f(x) = ax + b and g(x) = cx + d,
where 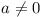 ,
, 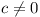 .
.
Now f(xf) = axf + b = xf (by defn.)  xf
= b/(1 - a),
xf
= b/(1 - a), 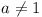 . Similarly, xg = d/(1 - c),
. Similarly, xg = d/(1 - c), 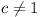 . Let F(x) =
f-1g-1fg(x) = x + (ad - bc + b - d)/ac (by
computation), (
. Let F(x) =
f-1g-1fg(x) = x + (ad - bc + b - d)/ac (by
computation), (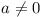 ,
, 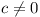 ). But by condition (i),
). But by condition (i), 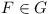 , and so by condition (iii),
there exists xF such that xF =
F(xF), i.e. xF = xF + (ad - bc + b -
d)/ac
, and so by condition (iii),
there exists xF such that xF =
F(xF), i.e. xF = xF + (ad - bc + b -
d)/ac  ad - bc + b
- d = 0
ad - bc + b
- d = 0  b/1-a =
d/1-c (
b/1-a =
d/1-c (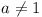 ,
, 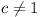 ), i.e. xf = xg.
), i.e. xf = xg.
But f and g were arbitrarily
chosen, so xf is constant for all 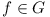 , i.e. there exists a real k so
that f(k) = k for all
, i.e. there exists a real k so
that f(k) = k for all 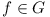 .
.
- Let
| bk | = | 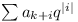 , the
summation being taken over all admissible i,
with , the
summation being taken over all admissible i,
with 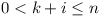 . . |
| = | a1qk-1 + a2qk-2 +
... + ak-1q + ak + ak+1q + ak+2k2 + ... +
anqn-k |
Then
- ak < bk is obvious (k =
1, 2, ..., n)
-
| qbk - bk-1 | = |
q(a1qk-1 + a2qk-2 + ... +ak-1q + ak
+ ak+1q + ... + anqn-k) |
| | - (a1qk + a2qk-1 +
... + ak-1q2 + akq + ak+1 + ... +
anqn-k-1) |
| = | (ak+1 + ak+2q +
... + anqn-k-1) (q2 - 1) < 0 |
and
| qbk+1 - bk | = |
q(a1qk + a2qk-1 + ... + akq + ak+1 +
ak+2q + ... + anqn-k-1) |
| | - (a1qk-1 + a2qk-2
+ ... + ak + ak+1q + ak+2q2 + ... +
anqn-k) |
| = | (q2 - 1) (a1qk-1 +
a2qk-2 + ... + ak) < 0. So (ii) is
proved. |
-
| b1 | + b2 + b3 + ... +
bn | = | a1 + a2q + a3q2 +
... | ... + anqn-1 |
| | | + a1q + a2 +
a3q + ... | ... +
anqn-2 |
| | | + a1q2 + a2q
+ a3 + ... | ... +
anqn-3 |
| | | ... | ... |
| | | ... | ... |
| | | a1qn-1 +
a2qn-2 + a3qn-3 + ... | ... +
an |
| = | a1(1 + q + q2 + q3 +
... + qn-1) + a2(q + 1 + q + q2) + |
| a3(q2 + q + 1 + q +
q2 + ... + qn-3) + |
| a4(q3 + q2 + q + 1 +
q + ... + qn-4) + ... + an(qn-1 + qn-2 + ... +
1) |
| < | (a1 + a2 + a3 +
... + an) (1 + 2q + 2q2 + 2q3 + ... + 2qn-1)
= |
| 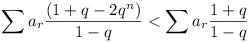 |
Other methods based on bk = Max(ak+i
q|i|), or Max(ai q|k-i|), a small
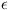 being to ensure
the strict inequality.
being to ensure
the strict inequality.
F.J.B.
Solutions reproduced from Science Teacher volume 17 number 3
(February 1974) pages 5 and 7.
I have been unable to locate the copyright holder of Science
Teacher; if you believe you own the copyright, please let me
know.
Return to IMO Register home page
Contact: Joseph Myers
(imo-register@imo-register.org.uk)
Online HTML version last updated:
5 January 2016
![]() where |OM|
denotes the length of the vector OM.
where |OM|
denotes the length of the vector OM.![]() there exist two other
points
there exist two other
points ![]() such that the straight lines AB and
CD are parallel and do not coincide.
such that the straight lines AB and
CD are parallel and do not coincide.![]() , and x
real, has the following properties:
, and x
real, has the following properties: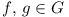 , then
, then 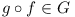 (where
(where 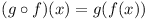 ), i.e. the set is closed under function
composition.
), i.e. the set is closed under function
composition.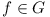 , then the
inverse function,
, then the
inverse function, 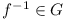 where f-1(x) = (x-b)/a for
f(x) = ax + b.
where f-1(x) = (x-b)/a for
f(x) = ax + b.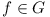 there exists an
there exists an 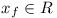 such that
f(xf) = xf.
such that
f(xf) = xf.![]() .
.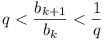 for all k from 1 to
n - 1.
for all k from 1 to
n - 1.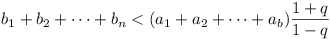
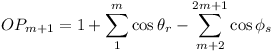 .
.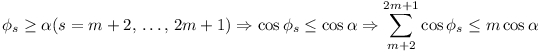 .
.![[diagram for question 1]](1973-fig0.png)
![[diagram for question 4]](1973-fig1.png)