INTERNATIONAL MATHEMATICAL OLYMPIAD 1974
Table 1. The British Team
| Marks | |
|---|
Michael P. Allen,
Woking County School for Boys. | 15 | |
Andrew B. Apps,
King’s School, Canterbury. | 37 | II |
Michael Beasley,
Kingston Grammar School. | 26 | III |
John E. Cremona,
The Perse School, Cambridge. | 24 | III |
Michael A. Gray,
The Perse School, Cambridge. | 17 | |
Richard C. Mason,
Manchester Grammar School. | 20 | |
David J. Seal,
Winchester College. | 22 | |
Antony J. Wassermann,
Royal Grammar School,
Newcastle-upon-Tyne. | 27 | III |
| 188 | |
II = 2nd prize III = 3rd prize
Table 2. The National Order.
| | Total
mark | Prizes |
|---|
| | I | II | III |
|---|
| 1. | Soviet Union | 256 | 2 | 3 | 2 |
| 2. | United States
of America | 243 | — | 5 | 3 |
| 3. | Hungary | 237 | 1 | 3 | 3 |
| 4. | German Democratic
Republic | 236 | — | 5 | 2 |
| 5. | Yugoslavia | 216 | 2 | 1 | 2 |
| 6. | Austria | 212 | 1 | 1 | 4 |
| 7. | Rumania | 199 | 1 | 1 | 3 |
| 8. | France | 194 | 1 | 1 | 3 |
| 9. | Great Britain | 188 | — | 1 | 3 |
| 10. | Sweden | 187 | 1 | 1 | — |
| 11. | Bulgaria | 171 | — | 1 | 4 |
| 12. | Czechoslovakia | 158 | — | — | 2 |
| 13. | North Vietnam | 146* | 1 | 1 | 2 |
| 14. | Poland | 138 | — | — | 2 |
| 15. | Netherlands | 112 | — | — | 1 |
| 16. | Finland | 111 | — | — | 1 |
| 17. | Cuba | 65* | — | — | — |
| 18. | Mongolia | 60 | — | — | — |
*Teams with less than eight members
Tables reproduced from Science Teacher volume 18 number 1 (October
1974) page 4.
16th INTERNATIONAL MATHEMATICAL OLYMPIAD 1974
DR. DAVID MONK, Deputy Leader of the British Team
Eighteen countries, the largest number ever, took part in the 16th
International Mathematical Olympiad in the German Democratic Republic
in July. Newcomers were the United States of America and North
Vietnam. Each country was represented by a team of eight school
students, accompanied by a leader and deputy leader.
The two contest sessions, each of four hours duration, were held at
the Pädagogische Hochschule “Dr. Theodor Neubauer”, a
teachers’ training college at Erfurt in which the teams were
accommodated. Erfurt, a city some 150 miles south-west of Berlin, is
a regional capital with various industries, situated in pleasant
countryside, and important as a horticultural centre.
Mr. Robert Lyness, the leader of the British team, took part in the
preliminary discussions on the Olympiad jury, at which the six contest
problems were selected. The team and deputy leader left London
(Victoria) on 5 July. We reached Erfurt punctually, and were greeted
by IMO representatives. A coach took us to the Hochschule, where a
friendly reception and a much-needed meal awaited us. There followed
a brief ceremony at which the British flag was raised alongside those
of other competing nations. Then the deputy leader left by car to
join the other deputies and leaders at the Interhotel
“Elephant” in Weimar.
Weimar, a smaller town about 12 miles east of Erfurt, is rich in
literary and musical associations. Goethe, Schiller and Liszt lived
there at various times and their houses are carefully preserved as
tourist attractions. Sightseeing interludes during the mathematical
activities therefore presented no problems! There is a College of
Architecture where the jury met, and working rooms were provided for
the delegations.
The day after their arrival was spent by the teams with sightseeing
in Erfurt and a youth concert. Meanwhile, the jury was settling fine
points of wording of the questions and checking the typescripts of the
papers. Strict precautions are always taken to preserve the
confidentiality of the questions and to ensure scrupulous fairness, so
the teams and their seniors did not mix at the opening ceremony.
Immediately afterwards, the first session began, and the leaders had
another duty—considering queries about the problems made in
writing by contestants. While they worked their deputies enjoyed
substantial “elevenses”!
Then, leaving the teams to their labours, the jury went on a coach
tour of Erfurt. Martin Luther studied and preached in the city, and
its sights include the Cathedral and the adjacent Severikirche. The
leaders’ exclusion from the earlier refreshments may have proved
an advantage at the next event on the jury programme—a sumptuous
lunch as guests of the Erfurt Regional Council!
By the time the jury returned to Weimar the scripts from the
day’s session were ready for marking. This, with the attendant
“co-ordination” and jury meetings to resolve difficulties
and assign prizes, was to occupy the leaders and deputies
intermittently for the next three and a half days. In addition the
leaders made another early journey to Erfurt to adjudicate on queries
at the start of the second session.
The scripts of each team are marked initially by its leader and
deputy leader. They are then scrutinised by co-ordinators. The
German mathematicians who performed this formidable task worked in
groups of three, each group dealing with just one question. Of all
the aspects of the generally excellent organisation of the Olympiad we
admired this most. The co-ordination was carried out with the
greatest courtesy and good humour, adhering to a carefully planned
timetable. Sometimes the co-ordinators were more generous than we
expected, occasionally a little stricter, but there was never any
difficulty in agreeing on a mark.
At the final reckoning, the British team was placed 9th in the
national order. Although naturally we should have liked a higher
place, it must be recognised that most of the other teams receive
coaching and preparation to an extent which we have not so far been
able to provide.
At its final meeting the jury agreed on the following inclusive
mark ranges for prizes: 38–40: 1st; 30–37: 2nd;
23–29: 3rd. This accorded with the custom of giving prizes to
about half the contestants. The rough guide-line is that the numbers
of 1st, 2nd and 3rd prizes should be in the ratios 1 : 2 : 3; the
actual numbers were 10, 24 and 37. As a result the British team took
one 2nd and three 3rds; the individual scores are listed in the first
table. Three contestants, from America, Hungary and Sweden, were
awarded prizes for special elegance. Six gained the maximum possible
mark of 40.
Special mention should be made of the performances by the two newly
participating countries. The Americans, to their great delight, came
second after Russia, beating the Hungarians and East Germans, always
strong contenders, into 3rd and 4th place respectively; every member
of the American team gained a prize. Only five Vietnamese competed
but four were prizewinners, including one 1st. The Cuban team, too,
was below strength, with seven members. The complete national order
is given in the second table.
A personal view is that the six questions were, on average, a shade
easier than those of recent Olympiads. If so, this probably reflects
the need to conform with the school syllabuses of an increasing number
of countries. Question 1 was particularly simple. Some of our team,
remarking on this, added the fair comment that two questions, numbers
1 and 4, had common features, involving systematic elimination of
cases.
Sightseeing and social events form an essential part of an IMO.
While the marking was in progress the teams had two full-day
outings—to Eisenach and a nearby castle, and to a textile
spinning mill—and a dance. After the last jury meeting came the
first excursion for teams and jury—to the former Buchenwald
concentration camp, situated just outside Weimar and now a national
memorial and museum. Here, among other similar ceremonies, Mr. Lyness
and the American leader, Professor S. L. Greitzer, laid wreaths on a
memorial to British and Canadian airmen.
On the following day, the entire personnel of the Olympiad
travelled by rail to (East) Berlin, the teams leaving Erfurt to the
accompaniment of farewell fanfares and singing, the seniors joining
the same train at Weimar. Again things were tightly organised.
Barely an hour after reaching our new accommodation—a hotel for
the jury, a university residence for the teams—we were off once
more, this time for a cruise through the rivers and lakes of Berlin,
with lunch on the boat. Sunday was devoted to an all-day visit to
Potsdam. Here we saw the Sanssouci Palace and the Cecilienhof, the
scene of the Potsdam Conference in July 1945. Some of the British
team were rebuked by a stern policewoman for crossing tramlines
without using the subway: fortunately their only brush with
authority!
The Berlin Kongresshalle was the setting for the closing ceremony
on Monday, 15 July. The prizewinners received their diplomas and
there were several addresses, including one by the only girl among the
winners, from Czechoslovakia. The orchestra of the
Georg-Friedrich-Hündel-Oberschule (a special school for the
musically talented) and a solo pianist provided musical interludes.
These formalities were followed in the evening by a cheerful farewell
dinner and entertainment. A day remained for local sightseeing,
including the breathtaking view of the city from the television tower.
Finally, on 17 July, the British contingent left by rail for the Hook
of Holland, the boat to Harwich and home.
The whole trip was constantly interesting and enjoyable. The
German organisers are to be congratulated on their arrangements and
warmly thanked for their helpfulness and hospitality, which has been
merely sketched in the foregoing paragraphs. Accepting the grave risk
of unfairness to others by naming just two persons, mention must be
made of Helmut Schreiber, our patient interpreter, and Professor
Wolfgang Engel of Rostock, the efficient and genial Chairman of the
Jury. As always, informal conversation between the various leaders
and deputies was a most valuable feature. The same may be said for
the teams, though in their case language difficulties were perhaps
more of an obstacle. Gifts were exchanged, and both team members and
seniors received from the organisers generous spending allowances for
the purchase of refreshment and souvenirs.
The 16th International Mathematical Olympiad has indeed set a high
standard for its successors to match! Both Bulgaria and Mongolia have
issued invitations to organise the 17th Olympiad. Moreover
“soundings” are being made on the possibility of Austria
being the host nation in 1976; this would be the first IMO to be held
in a non-Communist country.
IMO Questions: see page 9
Report reproduced from Science Teacher volume 18 number 1 (October
1974) page 5.
Three Qs were taken in two sessions on succeeding days. Time
allowed for each session was four hours. The country of origin of the
Q and the number of marks for it appear in brackets, e.g. (USA:
5).
-
Three players A, B and C play the following game: On each of
three cards an integer is written. These three numbers
p, q, r satisfy
0 < p < q < r.
These three cards are shuffled and dealt so that each player
has a card. Each then receives the number of counters indicated
by the card he holds. Then the cards are shuffled again; the
counters remain with the players.
This process (shuffling, dealing, giving out counters) takes
place for at least two rounds. After the last round A has 20
counters in all, B has 10 and C has 9. At the last round B
received r counters. Who received q
counters on the first round? (USA: 5)
-
In the triangle ABC, prove that there is a point
D on the side AB such that
CD is the geometric mean of AD and
DB if and only if
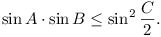
(Finland: 6)
-
Prove that the number
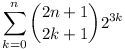
is not divisible by 5 for any natural number
n.
(Romania: 8)
-
Consider decompositions of an 8 × 8 chessboard into
p non-overlapping rectangles subject to the
following conditions:
- Each rectangle is to have as many white squares as black
squares.
- If ai is the number of white squares in the
i–th rectangle, then a1
< a2 < ... < ap.
Find the maximum value of p for which such a
decomposition is possible. For this value of p,
determine all possible sequences, a1,
a2, ..., ap.
(Bulgaria: 6)
-
Determine all possible values of
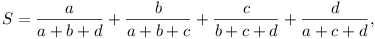
when a, b, c,
d are arbitrary positive numbers.
(Netherlands: 7)
-
Let P be a non-constant polynomial with integer
coefficients. If n(P) is the number of distinct
integers k such that [P(k)]2 = 1,
prove that 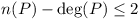 , where deg(P)
denotes the degree of the polynomial P.
, where deg(P)
denotes the degree of the polynomial P.
(Sweden: 8)
Questions reproduced from Science Teacher volume 18 number 1
(October 1974) page 9.
I have been unable to locate the copyright holder of Science
Teacher; if you believe you own the copyright, please let me
know.
Return to IMO Register home page
Contact: Joseph Myers
(imo-register@imo-register.org.uk)
Online HTML version last updated:
5 January 2016
![]()
![]()
![]()
![]() , where deg(P)
denotes the degree of the polynomial P.
, where deg(P)
denotes the degree of the polynomial P.