International Mathematical Olympiad, 1975
J. H. DURRAN
Winchester College

Shake the kaleidoscope. Visas and traveller’s cheques; the anxious meeting at Cromwell Road (so these are our companions for the next twelve days); the Danube from 29,000 ft; Bulgarians trotting into Sofia airport lounge by the OUT door; the pound-stokinki exchange rate (look again! stokinki?) 2.72 to the pound, Euler’s e; the heat; the friendly interpreter-companion; the traumatic isolation of team from jury at Burgus; the free pocket-money issue.

The final wording of the lucky six questions, chosen from dozens; prams and citizens promenading the Burgus boulevards in the cool of the evening; the open churches and a wedding; eating in a PECTOPAHT (transliteration from Cyrillic left as an exercise for the reader); never a dog.

The Opening Ceremony; flags of the nations; the heat; delay from lights failure; the heat; the start of the first four-hour session; tension in the jury room as questions on the questions are brought up to be answered or shrugged off; the heat; ice-cream, Coca-Cola, coffee rounds; only an hour to go.

See blue Black Sea (black Blue Danube we never see close); the inscrutable Mongolians, the smiling Vietnamese (they have something to smile about); sunflowers by the square mile (sorry: hectare); beaches, waves, sand, Golden Sands, Sunny Beach, tower hotels. The second session.

Marking, coordinating, discussing prizes; the jury’s turn on the rack; three days of that; but beaches again for the teams; and again the beaches.

The two-day cavalcade to Sofia; the competitors’ buses, police-escorted, holding the middle of the road; headlights glaring at noon; into the verge with oncoming traffic. The Balkan range and age-old passes, the invader’s way; yoghourt; the Turks and 1875; the welcomes in the towns; bouquets of carnations, roses; children with gifts; platforms, speeches (marguerites in the smaller towns); attar of roses, Thracian tomb. Turnovo, the Ancient Capital, with cyclopean gatehouse and Baldwin’s Tower; (breathless? weren’t we all?); fruit juices versus Coca-Cola; Roman inscriptions (a far cry from Hadrian’s Wall, the bounds of Empire, but Babel now); the Russian learner speaking his Russian to real live Russians with dust on their shoes.

Sofia; The Holy Wisdom and many-domed, golden-domed Alexander Nevsky; 1875 and the Turks; pink and peach stucco; Party HQ; cool mosque, the last of its tribe; Lenin’s frown; ancient churches; frescoes; bookshops; a dog (on a lead). The Closing Ceremony (already?); the prizes, hand-tooled leather folders; photographs; hands clasped; the partings of friends, photographs; the final dinner, 200 seated in a mountain-top restaurant; a double-bill farewell speech with American speaking Russian and Russian English (the night of space-craft rendezvous); dancing, more speeches; more wine (beer for the boys).

Sofia airport again; Vienna, only the airport (too far to the city, but a pastry, surely, and a coffee? At over £1?); IMO’s to be here next year, perhaps they’ll be free then? Heathrow; the bonds slip away; the crowds suck us in; ‘See you in October’, ‘Come and visit me’, ‘We’ll look at my slides’.

What was the mathematics like? The what? Oh, the mathematics; there were puzzles, tricks, in-jokes, chess; the official part was like this:

1. Let x_i, y_i (i = 1 to n) be real numbers such that

   

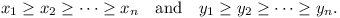
   Prove that, if z₁, z₂, ..., z_n is any permutation of y₁, y₂, ..., y_n, then

   

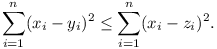
   (6 pts)

2. Let a₁, a₂, ..., a_r .. be any infinite sequence of strictly positive integers such that a_r < a_r + 1 for 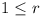. Prove that infinitely many a_n can be written in the form

   a_n = xa_i + ya_j

   with x, y strictly positive, and .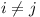

   (7 pts)

3. On the sides of an arbitrary triangle ABC, triangles ABR, BCP, CAQ are constructed externally with

   ,

   ,

   .

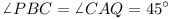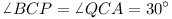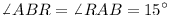   Prove that 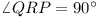and QR = RP.

   (7 pts)

4. When 4444⁴⁴⁴⁴ is written in decimal notation, the sum of its digits is A. Let B be the sum of the digits of A. Find the sum of the digits of B. (A, B are written in decimal notation.)

   (6 pts)

5. Determine, with proof, whether one can find 1975 points on the circumference of a circle of unit radius such that the distance (along the chord) between any two of them is a rational number.

   (6 pts)

6. Find all polynomials P in two variables with the following properties:

   1. for some positive integer n and all real t, x, y,

      P(tx, ty) = tⁿP(x, y)

      (that is P is homogeneous of degree n), and

   2. for all real a, b, c

      P(a + b, c) + P(b + c, a) + P(c + a, b) = 0,

      and

   3. P(1, 0) = 1.

   (8 pts)

Countries of origin:
1. Czechoslovakia, 2. Great Britain, 3. Netherlands, 4. USSR, 5. USSR, 6. Great Britain.

Our scores (out of 40) were 40, 40, 36, 32, 25, 24, 23, 19; we got 2 first prizes (only 8 competitors scored 40), 2 second prizes, 3 third prizes. As a team (team? the Olympic spirit?) we were 5th, 19 points behind the Hungarian winners, and the 7th team trailed us by 47 points.

Enter the NMC*, O reader; get chosen for the BMO; try for the XVIIIth IMO in Austria, 1976.

* National Mathematical Contest.

British Mathematical Olympiad.

Reproduced with permission from Mathematical Spectrum volume 8 (1975–6) pages 37–39
© 1976 Applied Probability Trust.

Return to IMO Register home page