The 18th International Mathematical Olympiad
COLIN GOLDSMITH
Marlborough College
The team from Great Britain to the olympiad held in Lienz, Austria
in July 1976 included four who had competed previously, so it was
expected to do well. In the event, we achieved our highest place ever,
second to the Soviet Union.
The competition, for teams of up to eight pre-university students,
consists of three questions to be tackled in a four-hour session on
one day followed by three more questions in a similar session on the
following day. Correct answers are not sufficient; close reasoning is
required and points are lost for any lapses in the rigour of a
proof. No charity is shown, with the result that only one student, a
Frenchman, scored full marks, one, a Russian girl, obtained 39 points
and 36 obtained a single-figure total out of a maximum of 40 points.
The results showing total scores for each team of eight competitors
are tabulated below:
| Question | | Prizes |
|---|
| 1 | 2 | 3 | 4 | 5 | 6 | Total | 1st | 2nd | 3rd |
|---|
| USSR | 36 | 46 | 46 | 46 | 31 | 45 | 250 | 4 | 3 | 1 |
| Great Britain | 23 | 35 | 52 | 43 | 11 | 50 | 214 | 2 | 4 | 1 |
| USA | 25 | 18 | 32 | 44 | 26 | 43 | 188 | 1 | 4 | 1 |
| Bulgaria | 22 | 18 | 37 | 36 | 6 | 55 | 174 | | 2 | 6 |
| Austria | 26 | 16 | 34 | 28 | 8 | 55 | 167 | 1 | 2 | 5 |
| France | 21 | 31 | 27 | 22 | 22 | 42 | 165 | 1 | 3 | 1 |
| Hungary | 27 | 15 | 19 | 38 | 8 | 53 | 160 | | 3 | 4 |
| East Germany | 26 | 18 | 28 | 27 | 12 | 31 | 142 | | 2 | 3 |
| Poland | 25 | 15 | 10 | 42 | 0 | 46 | 138 | | | 6 |
| Sweden | 19 | 0 | 38 | 27 | 0 | 36 | 120 | | 1 | 3 |
| Rumania | 18 | 10 | 13 | 28 | 1 | 48 | 118 | | 1 | 3 |
| Czechoslovakia | 22 | 11 | 13 | 30 | 7 | 33 | 116 | | 1 | 3 |
| Yugoslavia | 26 | 10 | 22 | 34 | 4 | 20 | 116 | | 1 | 3 |
| Vietnam | 21 | 9 | 15 | 29 | 10 | 28 | 112 | | 1 | 3 |
| Holland | 15 | 6 | 9 | 27 | 5 | 16 | 78 | | | 1 |
| Finland | 9 | 3 | 11 | 10 | 0 | 19 | 52 | | | 1 |
| Greece | 2 | 8 | 14 | 12 | 1 | 13 | 50 | | | |
| Maximum | 40 | 56 | 64 | 48 | 56 | 56 | 320 | | | |
In addition, Cuba entered three competitors and West Germany made a
trial appearance for the first time, with two students.
It is interesting to note how each country fared on each question,
the variations reflecting the different mathematics syllabuses in
operation. Calculus is not in the school syllabus in many of the
Eastern European countries, so no questions requiring calculus are set
in the IMO. However, a knowledge of calculus was used to advantage by
many competitors in Question 2, and this partly explains the
relatively good showing of the British team on this difficult
question. On the other hand, one was more likely to find the best
solution to Question 4 if no calculus was known. Similarly, some
experience of linear algebra proved a real disadvantage in Question 5
which can only be solved successfully by combinatorial methods. A
pragmatic approach works well with Question 3, equations and formal
argument being used only after considerable numerical investigation;
it was here that the British were most effective.
Like other international contests, the IMO aims to foster goodwill
and interchange of ideas and information between team members and
officials. This year’s olympiad certainly fulfilled these objectives,
due in no small part to the beauty of the surroundings in the Tyrol,
the imaginative organisation of our Austrian hosts and their
exceptional generosity.
All countries face the problem of providing stimulus and suitable
tuition for the mathematically gifted, often within a more or less
comprehensive system of education and usually without the
specialisation we are accustomed to in the sixth form. Some (e.g. the
Soviet Union and Yugoslavia) have special mathematical
schools. Regional and national competitions go some way to identify
and encourage talent, and the chance to represent one’s country on an
enjoyable trip abroad is a further carrot. Tuition by correspondence
is used in some countries and most hold training sessions for their
IMO teams. (The USA team had three weeks preparation together
immediately prior to the olympiad.) Here we have in the past provided
no special training and the team has met for the first time at the
start of the journey to the olympiad. This year for the first time
some problems have been sent at intervals by post to those requesting
them, solutions being provided with the next problems. Any British
school or sixth-former wishing to take advantage of this service
should write to Mr R. C. Lyness, Singleton Lodge, Blackpool FY6 8LT,
enclosing a stamped self-addressed envelope.
Appendix 1
The questions in the 1976 olympiad were as follows.
-
(5 points) In a plane convex quadrilateral of area 32
cm2 the sum of the lengths of two opposite sides and
one diagonal is equal to 16 cm.
Determine all possible lengths of the other diagonal.
-
(7 points) Let P1(x) =
x2 - 2 and Pj(x)
=
P1(Pj - 1(x))
for j = 2, 3, .... Show that, for any positive integer
n, the roots of the equation
Pn(x) = x are all real and
distinct.
-
(8 points) A rectangular box can be filled completely with unit
cubes. If one places as many cubes as possible, each with volume
2, in the box so that their edges are parallel to the edges of the
box, one can fill exactly 40 per cent of the box. Determine the
interior dimensions of all such boxes. (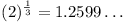 .)
.)
-
(6 points) Determine, with proof, the largest number which is
the product of positive integers whose sum is 1976.
-
(7 points) Consider the system of p equations in
q unknowns, where q = 2p,
a11x1 + ... +
a1qxq = 0,
a21x1 + ... +
a2qxq = 0,
...
ap1x1 + ... +
apqxq = 0,
with every coefficient aij a member of
the set { -1, 0, +1 }. Prove that there exists a solution
(x1, ..., xq) of the
system such that
- all xj (j = 1, ...,
q) are integers;
- there is at least one value of j for which
 ;
;
 (j = 1, ...,
q).
(j = 1, ...,
q).
-
(7 points) A sequence {un} is defined
by u0 = 2, u1 = 5/2,
un + 1 =
un(un - 12
- 2) - u1 for n = 1, 2, ....
Prove that, for positive integers n,
[un] =
2p, where 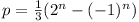 ,
,
and [x] denotes the greatest integer 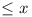 .
.
Appendix 2
Special prizes may be given by the international jury for solutions
of particular merit. One only was awarded this year, and this went to
J. R. Rickard (City of London School) for generalising the result of
Question 5 in the following way.
If ‘q = 2p’ is replaced by ‘q = kp,
k > 1’, and the restriction that  is replaced by ‘aij is an
integer with
is replaced by ‘aij is an
integer with 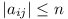 ,
, 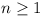 ’, then there
exists a solution satisfying (a), (b) and
’, then there
exists a solution satisfying (a), (b) and
(c') 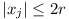 , where r is the least
integer greater than or equal to
½(nq)1 / (k - 1).
, where r is the least
integer greater than or equal to
½(nq)1 / (k - 1).
His proof of the original problem, suitably modified for the
generalised problem, went as follows.
Consider the ways of assigning -r, -r + 1, ..., -1,
0, 1, ..., r to each of x1, ...,
xq. There are (2r +
1)q such ways.
For each of these, L1, ..., Lp,
the values of the left-hand sides of the equations are such that 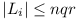 . So there are at most (2nqr +
1)p different sets of values for
L1, ..., Lp. Now
. So there are at most (2nqr +
1)p different sets of values for
L1, ..., Lp. Now
2r + 1 >
(nq)1 / (k - 1),
i.e.
(2r + 1)k - 1 >
nq,
and therefore
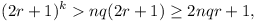
so that
(2r + 1)q > (2nqr +
1)p.
From the pigeon-hole principle it follows that there exist two
distinct sets of values for x1, ...,
xq which give the same set of values for
L1, ..., Lp. Call these
y1, ..., yq and
z1, ..., zq. Then
Xi = yi -
zi is easily seen to give a set of integer
values which satisfy the original equations. Moreover,
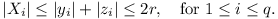
Reproduced with permission from Mathematical Spectrum volume 9
(1976–7) pages 37–40
© 1977 Applied Probability Trust.
Return to IMO Register home page
Contact: Joseph Myers
(imo-register@imo-register.org.uk)
Online HTML version last updated:
5 January 2016
![]() .)
.) ;
; (j = 1, ...,
q).
(j = 1, ...,
q).![]() ,
,![]() .
.