The 19th International Mathematical Olympiad
T. J. HEARD
City of London School
At Belgrade, in July 1977, 156 pre-university students from 21
countries competed in the 19th International Mathematical Olympiad.
Each delegation submits problems in advance, which are considered by
all the leaders just before the competition, when a final selection of
six is agreed. On two successive days the competitors tackle three
problems in four hours. Their scripts are assessed first by the
team’s leader and his deputy, who then discuss the solutions of each
problem with two Yugoslav coordinators whose task is to maintain a
common standard for that one problem. The few cases where
coordinators and leaders disagree on the value of a solution are
considered by the whole jury, a wearying process when conducted in
five languages on a hot afternoon.
The total scores (maximum 320) and prizes for each team of eight
were as shown in Table 1.
This year’s British team had only one overlap with last year’s, and
included two representatives from Scotland and one from Northern
Ireland. The team’s position has been bettered only once in the
eleven years in which we have taken part (second in 1976, though then
we were 36 points behind the winners, compared with 12 points this
year). One individual deserves particular mention: John Rickard (City
of London School), a team member for the third time, scored full marks
and received two special prizes for generalisations of problems. This
unique achievement was rightly acclaimed at the closing ceremony.
Of course there is much more to an international gathering like
this than the hard grind of the competition. Although the teams and
leaders came together only for the last two days, when assessment had
been completed, both groups were well entertained by our generous and
efficient Yugoslav hosts, with excursions, receptions, concerts, a
simultaneous chess display (where Richard Borcherds of King Edward’s
School, Birmingham, was one of only three to beat the Yugoslav grand
master), and time for making friends and learning about other
countries.
The degree of national support which the teams receive varies
widely. The selection of teams always seems to start with regional or
national competitions, such as our National Mathematics Contest and
British Mathematical Olympiad, though often these competitions are
much more part of the normal curriculum than they are here. We were
told that the selection of this year’s teams had involved some three
million pupils. Some countries (e.g. USSR and Yugoslavia) have
special mathematical schools catering for those who are successful.
Others select a pool of ‘possibles’ who are given training either by
correspondence or at regular weekend or holiday sessions, and from
whom the team is chosen. Of all the full teams the British, who met
for the first time at Heathrow, seem to have the least preparation.
This makes their good results all the more praiseworthy, but it also
prompts one to wonder whether with a modest extra effort we could not
win.
TABLE 1
| | | Prizes |
|---|
| Place | | Total | 1st | 2nd | 3rd | Special |
|---|
| 1 | USA | 202 | 2 | 3 | 1 | |
| 2 | USSR | 192 | 1 | 2 | 4 | 1 |
| 3= | Great Britain | 190 | 1 | 3 | 3 | 2 |
| 3= | Hungary | 190 | 1 | 3 | 2 | 1 |
| 5 | Netherlands | 185 | 1 | 2 | 3 | |
| 6 | Bulgaria | 172 | | 3 | 3 | |
| 7 | West Germany | 165 | 1 | 1 | 4 | |
| 8 | East Germany | 163 | 2 | 1 | 1 | 1 |
| 9 | Czechoslovakia | 161 | | 3 | 2 | 1 |
| 10 | Yugoslavia | 159 | | 3 | 3 | |
| 11 | Poland | 157 | 1 | 2 | 2 | |
| 12 | Austria | 151 | 1 | 1 | 2 | |
| 13 | Sweden | 137 | 1 | 1 | 2 | |
| 14 | France | 127 | 1 | | | |
| 15 | Rumania | 122 | | 1 | 2 | |
| 16 | Finland | 88 | | | 1 | |
| 17 | Mongolia | 49 | | | | |
In addition, teams of fewer than eight from Cuba, Belgium, Italy
and Algeria came 18th to 21st respectively. Greece and Vietnam had to
withdraw at the last moment.
Appendix
These were the problems for 1977.
-
(6 points) Equilateral triangles ABK, BCL,
CDM, DAN are constructed inside the square
ABCD. Prove that the midpoints of the four segments
KL, LM, MN, NK and the midpoints of
the eight segments AK, BK, BL, CL,
CM, DM, DN, AN are the twelve vertices
of a regular dodecagon.
-
(6 points) In a finite sequence of real numbers the sum of any
seven successive terms is negative and the sum of any eleven
successive terms is positive. Determine the maximum number of
terms in the sequence.
-
(7 points) Let n be a given integer > 2, and let
Vn be the set of integers 1 + kn,
where k = 1, 2, .... A number  is called
indecomposable in Vn if there do
not exist numbers
is called
indecomposable in Vn if there do
not exist numbers 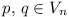 such that pq =
m. Prove that there exists a number
such that pq =
m. Prove that there exists a number 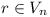 that can be expressed as the product of elements
indecomposable in Vn in more than one
way. (Expressions which differ only in the order of the elements
of Vn will be considered the same.)
that can be expressed as the product of elements
indecomposable in Vn in more than one
way. (Expressions which differ only in the order of the elements
of Vn will be considered the same.)
-
(6 points) a, b, A, B are given
constant real numbers, and
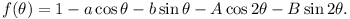
Prove that, if 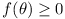 for all real
for all real
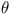 , then
, then
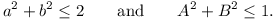
-
(7 points) Let a and b be positive integers.
When a2 + b2 is divided by
a + b the quotient is q and the remainder is
r. Find all pairs (a, b), given that
q2 + r = 1977.
-
(8 points) Let f(n) be a function defined on the
set of all positive integers and taking on all its values in the
same set. Prove that, if f(n + 1) >
f(f(n)) for each positive integer n,
then f(n) = n for each n.
Reproduced with permission from Mathematical Spectrum volume 10
(1977–8) pages 37–39
© 1978 Applied Probability Trust.
Return to IMO Register home page
Contact: Joseph Myers
(imo-register@imo-register.org.uk)
Online HTML version last updated:
5 January 2016
![]() is called
indecomposable in Vn if there do
not exist numbers
is called
indecomposable in Vn if there do
not exist numbers ![]() such that pq =
m. Prove that there exists a number
such that pq =
m. Prove that there exists a number ![]() that can be expressed as the product of elements
indecomposable in Vn in more than one
way. (Expressions which differ only in the order of the elements
of Vn will be considered the same.)
that can be expressed as the product of elements
indecomposable in Vn in more than one
way. (Expressions which differ only in the order of the elements
of Vn will be considered the same.)![]()
![]() for all real
for all real
![]() , then
, then![]()