The 21st International Mathematical Olympiad
COLIN GOLDSMITH
Marlborough College
Readers of Mathematical Spectrum will have seen reports of
previous years’ contests, which are for teams of up to eight
pre-university students. New and old readers will appreciate the
tough nature of the Olympiad if they settle down and tackle the
questions, allowing about an hour for each.
A record number of countries (23) were represented, including for
the first time Brazil, Israel and Luxembourg. The results of the
leading nations were as shown in the table.
| Competitor number | Total | Prizes |
|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | | 1st | 2nd | 3rd | Special |
|---|
| U.S.S.R. | 19 | 27 | 35 | 34 | 36 | 40 | 36 | 40 | 267 | 2 | 4 | 1 | |
| Romania | 35 | 23 | 17 | 33 | 32 | 28 | 39 | 33 | 240 | 1 | 4 | 2 | |
| West Germany | 21 | 14 | 35 | 33 | 39 | 30 | 34 | 29 | 235 | 1 | 5 | 1 | |
| United Kingdom | 23 | 23 | 34 | 30 | 32 | 34 | 21 | 21 | 216 | | 4 | 4 | |
| U.S.A. | 17 | 9 | 27 | 17 | 39 | 24 | 32 | 34 | 199 | 1 | 2 | 2 | |
| Vietnam | 32 | 29 | 33 | 40 | | | | | | 1 | 3 | | 1 |
| East Germany | 33 | 13 | 31 | 20 | 19 | 19 | 26 | 19 | 180 | | 2 | 2 | |
| Czechoslovakia | 16 | 20 | 24 | 17 | 23 | 40 | 12 | 26 | 178 | 1 | | 4 | |
| Hungary | 15 | 20 | 16 | 18 | 34 | 22 | 17 | 34 | 176 | | 2 | 2 | |
| Yugoslavia | 13 | 27 | 13 | 11 | 23 | 26 | 24 | 35 | 172 | | 1 | 4 | |
Since this year’s Olympiad was held for the first time in Britain,
it is appropriate to describe some of the arrangements. The various
countries had sent in 80 possible questions altogether. A short list
of 26 was made by Dr T. Fletcher, Dr D. Monk and Mr R. Lyness, and
these were discussed by the team leaders, with Dr Fletcher as
chairman, three days before the competition. This process went
exceptionally smoothly, and the final choice of six questions emerged
without serious disagreement. Since all the really hard questions
were voted against and question 3 was subsequently eased considerably
when the detailed wording was considered, the papers were ultimately a
little less testing than usual and seven students obtained full marks
or only dropped one point.
The competitors were housed in Westfield College, London, and the
domestic side, travel and entertainment were all administered by the
School Mathematics Project under an organizing committee set up by the
National Committee for Mathematical Contests. Special mention must go
to Mr J. Hersee who was in charge of all these aspects. Group visits
were made to Hampton Court, Greenwich (by boat), Windsor Castle and
Stratford, and the interpreter-guides attached to each team took their
students on further sightseeing and shopping trips to central London.
A most lively concert was put on by the Royal Academy of Music, and an
enjoyable reception was held by the Greater London Council on the
terrace of County Hall, with a steel band playing. Two nights at the
end were spent in Oxford.
All previous Olympiads have been government financed. This one was
the responsibility of the School Mathematics Project. The Department
of Education and Science made a substantial contribution, and generous
amounts were given by the Royal Society, the British Council and
various firms and schools. Dr B. Thwaites chaired the organizing
committee and was primarily responsible for finance.
The Olympiad was officially opened by Sir James Hamilton, Permanent
Secretary of the DES. The prizes were presented by the Duchess of
Gloucester, and a message from the Duke of Edinburgh was read at the
formal dinner at which the guests of honour were representatives of
the sponsors.
We can congratulate ourselves on the relaxed and efficient staging
of the 21st IMO, which was patently enjoyed by the teams and their
leaders. The British team were admirable hosts, and it was gratifying
that they were the only team to secure eight prizes.
The six questions were:
-
Let p and q be natural numbers such that
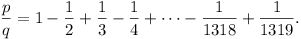
Prove that p is divisible by 1979.
-
A prism with pentagons
A1A2A3A4A5
and
B1B2B3B4B5
as top and bottom faces is given. Each side of the two pentagons
and each of the line-segments
AiBj, for all
i, j = 1,... , 5, is coloured either red or green.
Every triangle whose vertices are vertices of the prism and whose
sides have all been coloured has two sides of a different colour.
Show that all 10 sides of the top and bottom faces are the same
colour.
-
Two circles in a plane intersect. Let A be one of the
points of intersection. Starting simultaneously from A two
points move with constant speeds, each point travelling along its
own circle in the same sense. The two points return to A
simultaneously after one revolution. Prove that there is a fixed
point P in the plane such that, at any time, the distances
from P to the moving points are equal.
-
Given a plane 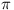 , a point P in this plane and a
point Q not in
, a point P in this plane and a
point Q not in 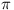 ,
find all points R in
,
find all points R in 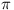 such that the ratio (QP +
PR)/QR is a maximum.
such that the ratio (QP +
PR)/QR is a maximum.
-
Find all real numbers a for which there exist
non-negative real numbers x1,
x2, x3, x4,
x5 satisfying the relations
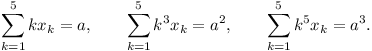
-
Let A and E be opposite vertices of a regular
octagon. A frog starts jumping at vertex A. From any
vertex of the octagon except E, it may jump to either of
the two adjacent vertices. When it reaches vertex E, the
frog stops and stays there. Let an be
the number of distinct paths of exactly n jumps ending at
E. Prove that
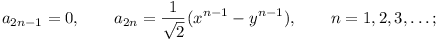
where 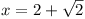 and
and
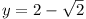 .
.
Note: A path of n jumps is a sequence of vertices
(P0, ..., Pn) such that
- P0 = A, Pn
= E;
- for every i,
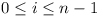 ,
Pi is distinct from E;
,
Pi is distinct from E;
- for every i,
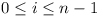 ,
Pi and
Pi + 1 are adjacent.
,
Pi and
Pi + 1 are adjacent.
Reproduced with permission from Mathematical Spectrum volume 12
(1979–80) pages 33–35
© 1980 Applied Probability Trust.
Return to IMO Register home page
Contact: Joseph Myers
(imo-register@imo-register.org.uk)
Online HTML version last updated:
5 January 2016
![]()
![]() , a point P in this plane and a
point Q not in
, a point P in this plane and a
point Q not in ![]() ,
find all points R in
,
find all points R in ![]() such that the ratio (QP +
PR)/QR is a maximum.
such that the ratio (QP +
PR)/QR is a maximum.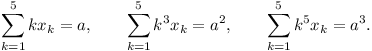
![]()
![]() and
and
![]() .
.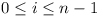 ,
Pi is distinct from E;
,
Pi is distinct from E;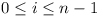 ,
Pi and
Pi + 1 are adjacent.
,
Pi and
Pi + 1 are adjacent.