28th INTERNATIONAL MATHEMATICAL OLYMPIAD
CUBA
1987
Report by Mr. Robert Lyness, Leader of the British Team
The Olympiad was held in Havana, Cuba from Sunday 5th July to
Thursday 16th July 1987. Forty two countries took part; generally
each delegation contained a Leader, Deputy Leader and a maximum of six
competitors. In the Appendix, a list of countries is given (with
their total marks). This list also shows the countries which had less
than six competitors. The total number of competitors was 236 (a
record high). About a dozen were girls.
Also attending were observers from Eire (to take part next year),
West Germany (to be host in 1989) and representatives of the Site
Committee from Great Britain, the USSR and Australia (host in
1988).
Travelling difficulties led to some delegations arriving and/or
departing early or late. Apart from the British Leader, who flew out
earlier, the British delegation travelled out on July 4th and returned
on July 15th. It contained Mr. Terry Heard (City of London School,
Deputy Leader), the six competitors and Mr. John Hersee (Secretary of
the IMO Site Committee).
The Jury met first on July 6th in a seaside hotel some 30
kilometres from the boarding school which housed all competitors.
Until July 11th, the Jury consisted only of Leaders. Deputies were
accommodated in a hotel in Havana and were in contact with
competitors. They joined the Jury after the second paper had been
taken.
The six problems were chosen by the Jury from those proposed by
participating countries, a preliminary selection having been made by a
subcommittee of the Cuban organizers. Once the questions were
settled, translated and typed out, the competitors had four-and-a-half
hours on each of two successive mornings to solve them. Then Leaders
and Deputies marked their team’s papers and submitted their
markings to Cuban co-ordinators. Terry Heard presented our scripts
excellently.
Prizes were awarded as follows: ‘1st prizes’ went to
each of the 22 competitors who attained a maximum total of marks, 42.
There were forty two ‘2nd prizes’ and fifty four
‘3rd prizes’. This meant that the British Team gained one
1st, two 2nd and two 3rd prizes. Our best performer, Kevin Buzzard,
scored full marks (42) and Andrew Smith dropped only one mark, with
41.
The prize-giving took place in a fine assembly hall. On the
platform were the Chairman of the Jury and members of the Site
Committee. Prize-winners went up in groups to be garlanded
simultaneously by the seated members – a much faster procedure
than usual. Following the prize-giving there was a concert of popular
music.
Our team was selected by means of the National Mathematics Contest
and the British Mathematical Olympiad, followed by some postal tuition
and a residential selection/training session which included a further
test. This session was held at the Ship Hotel, Reading from Friday
8th May to Sunday 10th May 1987. It was staffed by Judita Cofman,
David Cundy, Terry Heard, John Hersee, Paul Woodruff, and myself. The
training programme consisted of short lectures and tutorial periods
during which the participants had opportunities to expound their own
solutions to problems. It proved extremely helpful. All these
activities are the responsibility of the Mathematical
Association’s ‘National Committee for Mathematical
Contests’.
A programme of non-mathematical events was provided including, for
the Leaders, a visit to the Botanical Gardens, an evening cocktail
party given by the President of the Assembly of the People’s
Power of Havana City in the courtyard of a beautiful ‘Spanish
colonial’ house, and a visit to Ernest Hemingway’s Cuban
Estate. With our teams, we went for the day to Playa Giron (by the
Bay of Pigs) and to a most enjoyable evening reception offered by the
Minister of Education of the Cuban Republic.
After a couple of days acclimatisation, the team found the
accommodation and food at the ‘V.I. Lenin School for Exact
Sciences’ perfectly adequate. There were good on-site
recreational facilities, especially for swimming, and several evening
entertainments, but some team members missed the freedom to explore
the neighbourhood and Havana. The layout of the dormitories and the
early arrival of many teams encouraged the mixing of nationalities
which produced an exceptionally relaxed and friendly atmosphere at the
school. The members of the British team got on well together: ideas
were swapped, eccentricities tolerated, and much mutual support and
encouragement given.
Our thanks are due to the Cuban organisers who succeeded in giving
us an interesting and enjoyable time. The purpose of improving
international understanding and friendship has been achieved.
Robert Lyness
APPENDIX
The British Team
| Question | 1 | 2 | 3 | 4 | 5 | 6 | Total | Prize |
|---|
James Angus
(Wells Cathedral School) | 1 | 3 | 0 | 5 | 0 | 7 | 16 | — |
Kevin Buzzard
(RGS, High Wycombe) | 7 | 7 | 7 | 7 | 7 | 7 | 42 | 1st |
Gareth McCaughan
(Lincoln Christ’s Hospital S) | 7 | 3 | 7 | 6 | 5 | 3 | 31 | 3rd |
George Russell
(King Edward’s S, Birmingham) | 7 | 0 | 7 | 7 | 7 | 4 | 32 | 2nd |
Andrew Smith
(City of London School) | 7 | 6 | 7 | 7 | 7 | 7 | 41 | 2nd |
Gerard Thompson
(St. George’s Coll, Weybridge) | 0 | 7 | 0 | 5 | 7 | 1 | 20 | 3rd |
| Total marks | 29 | 26 | 28 | 37 | 33 | 29 | 182 | |
| | | | | | | out of a maximum
total of 252 |
Team Totals
| Romania | 250 | Australia | 143 | Colombia | 68 |
| W. Germany | 248 | Canada | 139 | Mongolia | 67 |
| USSR | 235 | Sweden | 134 | Poland (3) | 55 |
| E. Germany | 231 | Yugoslavia | 132 | Iceland (4) | 45 |
| USA | 220 | Brazil | 116 | Cyprus | 42 |
| Hungary | 218 | Greece | 111 | Peru | 41 |
| Bulgaria | 210 | Turkey | 94 | Italy (4) | 35 |
| China | 200 | Spain | 91 | Algeria | 29 |
| Czechoslovakia | 192 | Morocco | 88 | Kuwait | 28 |
| Great Britain | 182 | Cuba | 83 | Luxembourg (1) | 27 |
| Vietnam | 172 | Belgium | 74 | Uruguay (4) | 27 |
| France | 154 | Iran | 70 | Mexico (5) | 17 |
| Austria | 150 | Norway | 69 | Nicaragua | 13 |
| Holland | 146 | Finland | 69 | Panama | 7 |
Numbers ( ) indicate teams of less than 6.
28 OLYMPIADA
INTERNACIONAL DE
MATHEMATICA – LA
HABANA, CUBA
First Day – July 10, 1987
-
Let pn(k) be the number of permutations of the
set { 1, ..., n }, 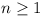 , which have exactly k fixed
points. Prove that
, which have exactly k fixed
points. Prove that
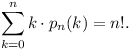
(Remark: A permutation f of a set
S is a one-to-one mapping of S onto
itself. An element i in S is called
a fixed point of the permutation f if f(i) =
i.)
-
In an acute-angled triangle ABC the interior
bisector of the angle A intersects
BC at L and intersects the
circumcircle of ABC again at N.
From point L perpendiculars are drawn to
AB and AC, the feet of these
perpendiculars being K and M
respectively. Prove that the quadrilateral AKNM
and the triangle ABC have equal area.
-
Let x1, x2, ...,
xn be real numbers satisfying x12 + x22
+ ... + xn2 = 1. Prove that for every integer 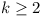 there are integers
a1, a2, ..., an,
not all 0, such that
there are integers
a1, a2, ..., an,
not all 0, such that 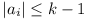 for all i and
for all i and
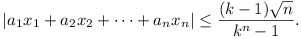
Second Day – July 11, 1987
-
Prove that there is no function f from the set
of non-negative integers into itself such that f(f(n)) = n
+ 1987 for every n.
-
Let n be an integer greater than or equal to 3.
Prove that there is a set of n points in the plane
such that the distance between any two points is irrational and
each set of three points determines a non-degenerate triangle with
rational area.
-
Let n be an integer greater than or equal to 2.
Prove that if k2 + k + n is prime for all integers
k such that 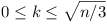 , then k2 + k + n is
prime for all integers k such that
, then k2 + k + n is
prime for all integers k such that 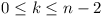 .
.
Time: 4.5 hours
Each problem is worth 7 points.
Return to IMO Register home page
Contact: Joseph Myers
(imo-register@imo-register.org.uk)
Online HTML version last updated:
5 January 2016
![]() , which have exactly k fixed
points. Prove that
, which have exactly k fixed
points. Prove that![]()
![]() there are integers
a1, a2, ..., an,
not all 0, such that
there are integers
a1, a2, ..., an,
not all 0, such that ![]() for all i and
for all i and![]()