INTERNATIONAL MATHEMATICAL OLYMPIAD 1988
Report
by Dr David Monk, Leader of the UK team
The Olympiad took place in Australia from 9th to 21st July 1988 and
was designated an Australian Bicentennial Event, with the Prime
Minister of Australia as Patron. The main venue was Canberra but
teams and leaders spent two or three days in Sydney on arrival.
The team reached Sydney on 10th July accompanied by Paul Woodruff
(Dulwich College), the Deputy Leader. I had arrived the previous day,
in accordance with the programme for leaders, and I accompanied the
team on the homeward journey, reaching London early on 25th July.
Three days outside the official Olympiad dates were spent in Australia
in order to take advantage of an excursion fare. Travel was by Qantas
and all arrangements went smoothly.
The organisation of the Olympiad was extremely efficient, with a
comprehensive programme of leisure activities to complement the
academic work. Innovations included visits by teams to schools,
students’ homes and to Embassies and High Commissions. There
was a special programme for “accompanying persons”. The
teams were accommodated, and the contest took place, at the Canberra
College of Advanced Education. The first part of the Jury’s
time was spent at University House and the Australian Academy of
Sciences building on the campus of the Australian National University.
The Jury moved to CCAE after the second examination. The team’s
accommodation in Sydney on arrival, and for the extra days, was at the
University of New South Wales.
The Jury met under the chairmanship of Professor Renfrey Potts of
the University of Adelaide, who guided its proceedings with friendly
efficiency. The selection, translation and typing of the problems
were completed well within the time allocated. Of the five problems
submitted by the United Kingdom, four were on the short list
preselected by the Jury, and one of these was among that
committee’s “starred” choices. This problem was
selected as number 3 for the Competition. Judged by the number of
contestants gaining the full mark of 7 for it, this proved to be the
second hardest problem. The decisions on prizes were also made
without undue difficulty. As Leader of a team submitting a contest
problem, I was a member of the subcommittee to adjudicate on special
prizes. Only one such prize was awarded, to a Bulgarian contestant
for his solution to the extremely difficult, but very interesting,
problem 6.
49 countries competed, several others being represented by
observers. Our team, with a total mark of 121, gained three second
prizes (Malcolm Law, Gareth McCaughan and Oliver Riordan) and two
third prizes (Cohn Bell and Christopher Nash). We were 11th in
“national order”, after USSR (217 out of 252), Romania
(201), China (201), West Germany (174), Vietnam (166), USA (153), East
Germany (145), Bulgaria (144), France (128) and Canada (124). This is
much the same position as in recent years. In an attempt to improve
it, we hope to improve our publicity to ensure that we attract the
best candidates available into our selection procedure and to make
some modifications to our tests.
Everybody greatly enjoyed the trip. Warmest thanks are due to the
Olympiad organisers under Mr Peter J O’Halloran for their
splendid arrangements and hospitality. I add especially my own thanks
to Paul Woodruff for his mathematical work and careful attention to
the well-being of the team. We are all most grateful to the sponsors
who made our participation possible.
D MONK
Department of Mathematics
University of
Edinburgh
September 1988
APPENDIX
The UK Team
| Question | 1 | 2 | 3 | 4 | 5 | 6 | Total | Prize |
|---|
Colin Bell
(Trinity School) | 1 | 7 | 7 | 0 | 5 | 0 | 20 | Bronze |
Malcolm Law
(King Edward’s S, Birmingham) | 5 | 7 | 2 | 1 | 7 | 1 | 23 | Silver |
Gareth McCaughan
(Lincoln Christ’s Hospital S) | 1 | 3 | 7 | 6 | 7 | 1 | 25 | Silver |
Christopher Nash
(King Edward’s S, Birmingham) | 7 | 7 | 1 | 1 | 1 | 2 | 19 | Bronze |
Oliver Riordan
(St. Paul’s School) | 7 | 7 | 1 | 7 | 4 | 1 | 27 | Silver |
Joshua Ross
(City of London School) | 1 | 3 | 1 | 1 | 0 | 1 | 7 | |
| Total marks | 22 | 34 | 19 | 16 | 24 | 6 | 121 |
| | | | | | | out of a maximum
total of 252 |
Team Totals
| USSR | 217 | Singapore | 96 | Italy (4) | 44 |
| Romania | 201 | Yugoslavia | 96 | Algeria (5) | 42 |
| China | 201 | Iran | 86 | Mexico | 40 |
| West Germany | 174 | Netherlands | 85 | Brazil | 39 |
| Vietnam | 166 | Republic of Korea | 79 | Iceland (4) | 37 |
| United States | 153 | Belgium | 76 | Cuba | 35 |
| East Germany (5) | 145 | Hong Kong | 68 | Spain | 34 |
| Bulgaria | 144 | Tunisia (4) | 67 | Norway | 33 |
| France | 128 | Colombia | 66 | Ireland | 30 |
| Canada | 124 | Turkey | 65 | Philippines (5) | 29 |
| United Kingdom | 121 | Greece | 65 | Kuwait | 23 |
| Czechoslovakia | 120 | Finland | 65 | Argentina (3) | 23 |
| Sweden | 115 | Luxembourg (3) | 64 | Cyprus | 21 |
| Israel | 115 | Morocco | 62 | Indonesia (3) | 6 |
| Austria | 110 | Peru | 55 | Ecuador (1) | 1 |
| Hungary | 109 | Poland (3) | 54 | |
| Australia | 100 | New Zealand | 47 | |
Numbers () indicate teams of less than 6.
XXIX INTERNATIONAL MATHEMATICAL OLYMPIAD
Canberra, Australia – July 1988
-
Consider two coplanar circles of radii R and
r (R > r) with the same centre.
Let P be a fixed point on the smaller circle and
B a variable point on the larger circle. The line
BP meets the larger circle again at
C. The perpendicular 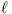 to BP at P
meets the smaller circle again at A (if
to BP at P
meets the smaller circle again at A (if 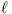 is tangent to the circle at P
then A = P).
is tangent to the circle at P
then A = P).
- Find the set of values of BC2 + CA2 + AB2.
- Find the locus of the midpoint of AB.
(Luxembourg)
-
Let n be a positive integer and let
A1, A2, ....,
A2n+1 be subsets of a set B.
Suppose that
- each Ai has exactly 2n
elements,
- each
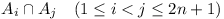 contains exactly one element, and
contains exactly one element, and
- every element of B belongs to at least two of
the Ai.
For which values of n can one assign to every
element of B one of the numbers 0 and 1 in such a
way that each Ai has 0 assigned to exactly
n of its elements?
(Czechoslovakia)
-
A function f is defined on the positive integers by
f(1) = 1, f(3) =
3
f(2n) = f(n)
f(4n+1) =
2f(2n+1) - f(n)
f(4n+3) = 3f(2n+1) -
2f(n)
for all positive integers n. Determine the
number of positive integers n, less than or equal
to 1988, for which f(n) = n.
(United Kingdom)
-
Show that the set of real numbers x which
satisfy the inequality
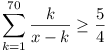
is a union of disjoint intervals, the sum of whose lengths is
1988.
(Ireland)
-
ABC is a triangle right-angled at
A, and D is the foot of the altitude
from A. The straight line joining the incentres of
the triangles ABD, ACD intersects
the sides AB, AC at the points
K, L respectively. S
and T denote the areas of the triangles
ABC and AKL respectively. Show that
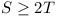 .
.
(Greece)
-
Let a and b be positive integers
such that ab + 1 divides a2 + b2.
Show that 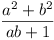 is the square
of an integer.
is the square
of an integer.
(West Germany)
Problems 1 – 3 first day; 4 – 6 second day. 4½
hours each day.
Each problem is worth 7 points.
Return to IMO Register home page
Contact: Joseph Myers
(imo-register@imo-register.org.uk)
Online HTML version last updated:
5 January 2016
![]() to BP at P
meets the smaller circle again at A (if
to BP at P
meets the smaller circle again at A (if ![]() is tangent to the circle at P
then A = P).
is tangent to the circle at P
then A = P).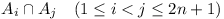 contains exactly one element, and
contains exactly one element, and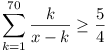
![]() .
.![]() is the square
of an integer.
is the square
of an integer.