32ND INTERNATIONAL MATHEMATICAL OLYMPIAD
SIGTUNA SWEDEN
12TH – 23RD JULY 1991
Each year the Leader of the UK IMO team writes a report for the
UK organising committee. This year’s report is slightly
different in that
- it is deliberately informal in style;
- it tries to summarise the whole sequence of events leading
from the NMC up to the IMO so that the reader can see how the
different stages interact:
- copies will be sent to all schools which took part in the BMO
in the hope that they will make their own copies for interested
colleagues, for students who took part in last year’s BMO,
and for those who might be interested in taking part in the coming
year;
- copies will also be sent to all who have contributed in some
way to the success of the 1990/1 UK Olympiad program.
It may be worth stressing that the UK organisation has changed
dramatically during 1991.
(1) The sequence of events from the BMO onwards is now run
by a committee – the British Mathematical Olympiad Committee
– which is entirely separate from the Mathematical
Association.
(2) The old MA committee which used to run everything
– the National Committee for Mathematical Contests – is
now responsible only for the NMC. They hope that, with
the introduction of certificates, improved publicity and more
attractive questions, the NMC will expand considerably in the years
ahead.
The BMOC had its first meeting in June this year and is in the
process of rethinking its strategy. (If you have any thoughts on how
you think the BMOC should develop its activities, please write to me
before 14th September 1991.)
Tony Gardiner, School of Mathematics,
University of Birmingham, B15 2TT
General Background
For many countries the International Mathematical Olympiad marks
the climax to their own domestic program of Mathematical Olympiads.
At the IMO, each country can enter up to six students. This year 318
students from 56 countries took part.
It is easy to dismiss an event which involves only six students
from each country as being irrelevant to most able
mathematicians. However, the students who represent each country are
chosen from a much larger group – namely all those who take part
in the various stages of that country’s national Olympiad
sequence. Most of these students do not expect to reach the final
six; they simply enjoy the experience of trying to solve unusual and
challenging problems up to the highest level they can reach.
Thus one should not view the IMO in isolation. The sequence of events
which leads up to the selection of the UK IMO team is intended to
stimulate and challenge a much larger group. In the process, hundreds
of students achieve remarkable results. All are to be congratulated.
Mathematicians come in all shapes and sizes, and develop in
different ways and at different rates. Olympiad competitions –
especially the experience of being completely stumped by harmless
looking problems – should encourage all of us to aim a little
higher. Some have shown by their success what they could
achieve in the future if they apply themselves; others have glimpsed a
world of hard but worthwhile problems which are at present beyond
their powers, but which – given time and effort – could be
mastered.
One member of this year’s IMO team illustrates this point to
perfection. Michael Fryers (Altrincham Grammar School) got into last
year’s team for the first time by the skin of his teeth. In the
1990 IMO in Beijing he acquitted himself well, but certainly not
outstandingly, by scoring 18 out of 42. Fortunately the team also
contained two students (Oliver Riordan from St Pauls and Vin de Silva
from Dulwich College) who showed just what could be achieved, scoring
40 and 39 respectively out of 42. The point was not wasted on young
Michael. Read on!
The UK Selection Process
On 30th November 1990 nearly 17000 students took the National
Mathematics Contest – a 1½ hour multiple choice paper
for students in their last two or three years at school. Almost 1000
of these received Gold certificates, 2000 received Silver and 3000
received Bronze.
On 16th January 1991 400 of the best students tackled seven
problems on the 3½ hour British Mathematical Olympiad.
Olympiad problems are not just hard A level problems: they force
students to think and cannot usually be solved by merely
applying the right standard method. For students who have been
trained on a diet of A level papers, and who have come to expect all
mathematical problems to be as predictable as A level questions, the
experience of facing genuinely hard problems for the first time can be
rather daunting.
When faced with a hard problem, it is always tempting to give up
too easily. But the important thing in any Olympiad (as in real
mathematics!) is not to give up, but to struggle on and to try
to solve one or two problems completely. Those who managed
this on the BMO had already achieved something substantial, even if it
was only the top 26 students who received book prizes.
In the light of each student’s performance in both the NMC
and the BMO (with more emphasis on the BMO score!) 60 students were
invited to take another 3½ hour paper (FIST) on February 28th
1991. This paper contained just four harder questions (though still
somewhat easier than real IMO problems). Those chosen were not simply
the top 60 students. Some allowance was made for age, since we felt
that some younger students who had shown notable promise needed the
experience of trying to solve mathematical problems at this level
under timed conditions.
Selection is always difficult. Limitations on numbers mean that we
often have to choose between individuals who cannot be easily
‘ranked’. We hope those we leave out appreciate this, and
find encouragement in what they have achieved rather than
disappointment at just missing out.
The next stage was to choose 20 students for a 3 day residential
“training” session held in Trinity College, Cambridge from
April 4th–7th 1991.
IMO problems are substantially harder than BMO or FIST problems, so
some kind of further preparation is essential. However, there is a
limit to how much one can achieve in just three days. As long as the
summer term continues to be dominated by public examinations, it is
hard to see how the UK team can do much by way of serious, intensive,
residential training. Thus, unlike many other countries, the UK has
little option but to look for ways of encouraging students to do their
own preparation in their own time.
The Cambridge session is very valuable in providing basic
instruction in Algebra, Combinatorics, Geometry, Inequalities, and
Number Theory, and general sessions on How to attack problems which
look horribly hard, or How to write out solutions. But if
the session is to bear fruit, participants must then go home and do a
lot more work on their own.
On the last morning of the training session the students take the
final selection test (SIST) after which the IMO team of six is
selected.
Many of those who are invited to the session have one or more years
left at school. We depend on these younger participants being
sufficiently motivated to go home and do the necessary extra work for
themselves. We are delighted that this year the younger students who
did not make this year’s IMO team have continued to send in
solutions to problems throughout the summer. We hope that next year
their sights will be set that much higher. But, above all, we hope
that they will have benefitted mathematically from what they have done
this year.
The 32nd International Mathematical Olympiad
This year’s UK IMO team consisted of
| Michael Fryers | (Altrincham Grammar School) |
| Oliver Johnson | (KES, Birmingham) |
| Robin Michaels | (Haberdashers Askes Boys School) |
| Luke Pebody | (Rugby School) |
| Adam Shepherd | (KES, Birmingham) |
| Stephen Wilcox | (Portsmouth Grammar School) |
The Team Leader was Tony Gardiner (University of Birmingham) and
the Deputy Leader Paul Woodruff (Dulwich College).
Having succeeded in our own Olympiad sequence these six students
were now faced with a much tougher challenge. The IMO problems they
were to face in Sweden in July would be harder than anything they had
seen up to that point. Moreover, the IMO requires not only
creativity, but also reliability: it is not enough that one could
in principle solve this or that problem – you have to be
able to come up with the right ideas there and then.
The six were encouraged to do all the preparation they could. But
with exams and other pressures, the only formal requirement was that
they should send in solutions to three IMO-type problems every two
weeks between late April and late June. The team also met in
Birmingham for 2½ days (3rd–5th July) to ‘warm
up’ and to generate a sense of communal purpose shortly before
leaving for Sweden.
The IMO competition consists of two 4½ hour papers taken on
successive mornings (17th and 18th July). Each paper contains three
problems, and each problem is worth 7 marks. The problems are tough,
and some are tougher than others. My guess is that most experienced
professional mathematicians would be lucky to solve two problems
completely and correctly on each day. Thus a score of more than 30 is
a remarkable achievement.
Many official contestants have the ‘advantage’ of
having had weeks of intensive preparation and training. If one is
going to enter an international competition of this type at the very
highest level, then it is sensible to do enough serious preparation to
allow one’s students to get the most out of taking part. This
is not quite as simple as it sounds. Olympiads are meant to
encourage the mathematical development of exceptional students.
There is obviously a danger that some countries may become so obsessed
with ‘success’ at the IMO that they will adopt intensive
training methods over long periods which may distort the
mathematical development of their best students. Most countries
understand this danger, and I was, on the whole, most impressed with
the sensitive way many countries select and prepare their teams: we
have a lot to learn from them.
Next we come to this year’s two IMO papers.
Paper 1
-
Given a triangle ABC, let I be
the centre of its inscribed circle. The internal bisectors of the
angles A, B, C meet
the opposite sides in A', B',
C' respectively. Prove that
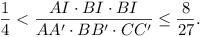
-
Let n > 6 be an integer and
a1, a2, ..., ak be
all the natural numbers less than n and relatively
prime to n. If
a2 - a1 = a3 - a2 = ... = ak -
ak-1 > 0
prove that n must be either a prime number or a
power of 2.
-
Let S = { 1, 2, 3, ..., 280 }. Find the
smallest integer n such that each
n-element subset of S contains five
numbers which are pairwise relatively prime.
Paper 2
-
Suppose G is a connected graph with
k edges. Prove that it is possible to label the
edges 1, 2, 3, ..., k in such a way that at each
vertex which belongs to two or more edges the greatest common
divisor of all the integers labelling those edges is equal to
1.
-
Let ABC be a triangle and P an
interior point in ABC. Show that at least one of
the angles 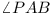 ,
,
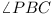 ,
, 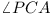 is less than or equal to
30°.
is less than or equal to
30°.
-
Given any real number a > 1, construct a
bounded infinite sequence x0, x1,
x2, ... such that
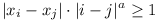
for every pair of distinct non-negative integers
i, j.
Of the six problems, Question 2 is probably the kindest (though it
may not look that way under IMO conditions).
Two of the problems (1 and 5) involve geometry and
inequalities (though in a very different way, and neither
problem involves much pure geometry). Any reasonably prepared
team from a country the size of the UK should have scored almost full
marks on these two problems, whereas we scored only 42 out of a
possible total of 84! There is plenty of scope here for improvement.
Our weakness in Question 5 (where we scored only 15 out of a possible
42) contrasts starkly with our performance on the very tough Question
3.
On Question 3 we scored a remarkable 26 out of a possible 42
– a score which was bettered only by USSR (34), FRG (33), China
(31), Hungary (30), Japan (28), and Roumania (27). This shows what
our students were capable of mathematically, and suggests that marks
were simply thrown away on Question 5.
Question 4 was an attempt to create a precedent, so that in future
questions explicitly involving graphs might be accepted as conforming
to the (unwritten!) IMO syllabus.
At the IMO roughly 1/12 of participants receive First Prizes
(=Gold medals), 1/6 receive Second Prizes (=Silver), and 1/4
receive Third Prizes (=Bronze). This year 20 students (those
with scores 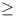 39/42)
received Gold, 51 students (those scoring
39/42)
received Gold, 51 students (those scoring 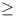 31)
received Silver, and 84 (those scoring
31)
received Silver, and 84 (those scoring 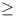 19)
received Bronze. There is also a category called Honourable
Mention for any participant who does not receive a medal but who
scores full marks for solving at least one problem completely and
correctly.
19)
received Bronze. There is also a category called Honourable
Mention for any participant who does not receive a medal but who
scores full marks for solving at least one problem completely and
correctly.
From time to time any country as big as the UK is bound to throw up
the odd truly exceptional student. If we are lucky we may even find
that our IMO team regularly contains at least one such student.
However, such students should not distract us from what I believe to
be the main task, which is to raise the performance of the
team’s lowest scoring member in a predictable
and controlled way. Too often good students go to the IMO and turn in
what one can only describe as a shell-shocked performance,
scraping up scores of 1, or 2 (and maybe one 3) on each question.
I believe we should concentrate our efforts in the immediate future
on devising ways of selecting and preparing students which will allow
us to reliably produce teams whose minimum score is in the low
20s.
I set this year’s UK IMO team a simple goal. I suggested
that all six students should aim at achieving either a medal or an
Honourable Mention. (Those who knew they should be aiming much
higher than this did not need to be told!) They worked hard
throughout the summer term, and I am delighted to be able to report
that they did exactly what I asked, at the same time raising the
minimum score to 17. Here are the results:
| Michael Fryers | 42 | (Gold) |
| Robin Michaels | 29 | (Bronze) |
| Stephen Wilcox | 20 | (Bronze) |
| Oliver Johnson | 17 | (H.M.) |
| Luke Pebody | 17 | (H.M.) |
| Adam Shepherd | 17 | (H.M.) |
It would have been nice to come home with six medals (Oliver, Luke,
and Adam missed Bronze by just 2 points, and Robin missed Silver by
the same margin). But their achievement should not be underestimated.
They deserve our hearty congratulations.
Clearly the most remarkable achievement is that of Michael Fryers
in obtaining a perfect score. Eight other students also scored full
marks: 4 from the Soviet Union, and 1 each from China, France,
Hungary, and Roumania. These are all remarkable students (for
example, Vincent Lafforgue from France also had a perfect score last
year, and one young girl from the Soviet Union – Evgeniya
Malinnikova – has had perfect scores for three years in a row).
But all, except possibly the student from France, have had the
advantage of intensive preparation provided by experienced adults. In
contrast, Michael’s success (like that of our two outstanding
students last year) is largely due to his own efforts. The enclosed
article celebrating his achievement comes from the Daily Telegraph of
25th July 1991.
The IMO is full of lovely surprises. One other outstanding
achievement was that of the young Swiss girl Bea Wollenmann. She
found out about the IMO only to discover that the Swiss had never
taken part. However she was so determined to go, that she chose her
own Team Leader, raised the money to get them both to Sweden, and went
home with a Bronze medal having achieved the second highest score by a
female participant!
How the 32nd IMO was run
That the IMO takes place at all is an annual miracle. It is not
run by any organisation, nor guided by any international quango. It
started in 1959 and for the first nine years was restricted to a small
group of East European countries (Bulgaria, Czechoslovakia, East
Germany, Hungary, Poland, Roumania, Soviet Union, and Yugoslavia).
Some of these had a long tradition of mathematical Olympiads: for
example, the Hungarian Eötvös competition started way back
in 1892. Moreover, theme countries all make a habit of encouraging
academics to work with and to write for bright High School students.
Just as we began to ignore our own 1944 Education Act with its bold
vision of providing for children “according to their
needs”, these rather different countries were busy taking the
challenge seriously.
In 1967 13 countries took part in the IMO, including for the
first time four western countries – among them the UK and
this year’s hosts Sweden. The 1979 IMO was held in London with
around 25 countries. The number of participating countries expanded
massively at the end of the 80s, and at this year’s IMO 56
countries took part, with 3 more having official Observers with
a view to joining in next year.
Each year one country agrees to act as host and is then responsible
for all expenses from the time teams arrive at the airport on Day 1 to
their departure after the IMO. This represents a substantial
commitment in both money and manpower, and I suspect that it takes the
host country three or four years to prepare for each IMO. This
year’s official hosts were the Swedish Mathematical
Society. They did a very fine job.
All practical arrangements clearly have to be made by the local
organisers long in advance. But the body with formal
responsibility
for choosing the problems
for marking the scripts and for approving the awards
for making any other relevant decisions
is the IMO Jury. This year’s Jury came into existence
on Day 2 (13th July) and ceased to exist on Day 11 (22nd July) at the
closing ceremony. Membership of the Jury is restricted to the Leaders
of Participating Countries for that year. Noone else is allowed to
vote (or to contribute in any way unless invited to do so).
How are the problems chosen? Each participating country is asked
to submit up to six problems of an appropriate standard. The
resulting collection is whittled down to a shortlist (this year of 30
problems) by a committee of experienced mathematicians from the host
country. The Jury could theoretically overturn their judgement, but
is usually extremely grateful for this preparatory work: without it
the delicate task of choosing problems agreeable to all
participating countries would be almost impossible. This year was no
exception. One valuable innovation this year was that on arrival,
members of the Jury were given the shortlisted problems but not the
solutions. This gave us 12 hours to work on the problems and to
decide for ourselves how hard, or how suitable, the problems were
without being distracted by ‘official’ solutions. (In
this time I managed to solve 8 or 9 of the problems and got a
reasonable impression of what the others involved.)
The Jury has to work quite hard. First unsuitable problems are
eliminated:
- problems which are much too hard or much too easy, or
- problems which will lead to solutions which will be impossible
to mark (in 36 different languages!), or
- problems which have already appeared somewhere in the
literature, or
- problems which have been used in previous competitions unknown
to the shortlisting committee, or
- problems which are very close to problems which one or more
countries have used during training.
Next problems which are popular with many Jury members are
identified. These are then classified as being either easyish,
middling, or hard. Roughly speaking, the Jury tries to
choose the first problem on each paper (Questions 1 and 4) to be
relatively straightforward, but feels free to make the third problem
each day (Questions 3 and 6) genuinely tough.
The whole system depends on trust and honesty. Team Leaders have
all worked long and hard with their teams and clearly want their team
to do as well as possible. With modern communications technology it
would be easy to cheat if one was determined to do so. Despite this,
the atmosphere in general struck me as being very open with remarkably
little petty rivalry. However, to help protect us from temptation,
the Jury arrives three days early and is held incommunicado at an
unknown location away from the teams while it does its work. This
year the Jury was based in Uppsala from July 12th–18th and had
completed most of its work before the teams arrived. The teams
arrived on July 15th and were housed in Sigtuna (50kms away!).
Once the 6 problems have been chosen and approved the Jury has to
agree on the precise wording of each question, and has to check and
approve versions in the five official languages – English,
French, German, Russian and Spanish. It is very important to get
these right, as countries whose students usually work in other
languages must then translate one of these official versions into
their own language. These translations must then be checked and
approved. This year there were 36 different language versions in
seven or eight different alphabets.
All this and other Jury business takes three very full days. On
July 16th, while the teams were settling in and the papers were being
duplicated for the following day, the Jury was taken off to visit a
famous 17th century ironworks and a 20th century nuclear power
station. After three days with our heads down, this provided
opportunities for Leaders and Observers to get to know each other more
informally and to share their experiences from running their own
national Olympiads and from training their own IMO teams. We returned
in the evening and dressed for the Opening Ceremony, which was held in
the main hall of Uppsala University. The University was founded in
1477 and is the oldest in northern Europe. The hall was built to
commemorate the 400th anniversary in 1877. For the Opening Ceremony
the Jury and the teams are kept strictly apart. I found this gave
rise to strange emotions. We were only too aware of what our teams
would face the very next morning. We had been an integral part of
their preparations, and would share in their success or failure. Yet
we were unable to join them!
The 56 teams had not yet had much opportunity to get to know each
other. Little could one imagine how different things would be Just
six days later at the Closing Ceremony, Banquet, and
Entertainment.
Two days later the teams had finished their hard work –
though ours had begun in earnest. The fact that each participant had
gone through fire along with 317 other students provided a common bond
which made it easier for groups of students from different cultural
backgrounds to discover that they were all made of the same flesh and
blood. The second exam was followed by a football knockout
competition in which flesh collided with flesh and blood flowed
freely. We were beaten 5–0 by Spain!
For some reason this particular encounter did not seem to blossom
into more cordial Anglo-Hispanic relations. But solid links were soon
forged with the Icelandic, the Irish, the New Zealand, the Australian
teams, and others. One UK team member invested a considerable amount
of effort pursuing a cuddly Koala, while another definitely preferred
Kiwi, and a third was rumoured to have played bridge continuously for
18 hours. The Canadians and Americans collected signatures on their
T-shirts, while a Slovenian wore a Slovenian independence T shirt to
collect his medal, explaining that – no matter what the official
program might say – he saw himself as representing Slovenia
rather than Yugoslavia.
The emerging patchwork of social interactions was only glimpsed by
the hard-driven Leaders and Deputy-Leaders who were now embroiled in
the process of marking and grading students’ scripts. The
logistics of coordinating and judging the marking of 6 problems from
each of 6 students from 56 countries in 36 languages – all in
less than 48 hours – is truly mind-boggling.
The Swedish judging process struck me as impressively firm and
admirably fair. I found the whole procedure – in which Leaders
have the responsibility to present their students’ solutions
clearly and in the best possible light to the judges, whose job it is
to ask all sorts of awkward questions to identify the weaknesses and
limitations of each solution before finally deciding on a mark –
a new and rewarding experience.
As each new set of marks (say, for the six UK students on Question
1) were approved, they were pinned up in the foyer of the main
building. The intense interest shown by students in the successes of
other countries as well as their own was quite moving.
On Friday afternoon our youngest student admitted that he had had a
curious pain in his lower stomach ever since Tuesday morning! He was
whisked off to hospital and diagnosed as having a twisted lower
intestine. Prompt action eventually avoided the need for surgical
intervention.
On Sunday all 450 students and staff were let loose on Stockholm.
We visited the impressive Vasa museum, went on a long harbour cruise,
and ambled through the narrow streets of the old town. Months of hard
work and preparation were at an end, and most of us drifted through
the day. We all had our successes (individuals or groups who had
excelled themselves, surpassing our expectations). And most of us
also had our disappointments. But there was nothing we could do now
except pick ourselves up slowly and begin to look ahead to what we
might do in the coming year.
On Monday most people went to Uppsala for the day. But some
preferred to enjoy their first leisurely breakfast, followed by a
stroll round Sigtuna itself – an old small town which was for
hundreds of years the capital of Sweden, until that role passed to
Uppsala and Stockholm. After lunch we packed and dressed for the
Closing Awards Ceremony, which was followed by the banquet and
entertainment in the City Theatre.
We returned to Sigtuna, happy but tired, around 11.30. Our bus to
the airport was to leave at 6.30 a.m., so a good night’s sleep
was already out of the question. I sat round talking to other Leaders
and Deputies, drinking tea (or was it Tequila? I forget.) until about
3.00 before going to bed. The students decided it was safer not to
got to bed at all!
I have enjoyed working with them and with all those who took part
in earlier rounds of our Olympiad program. I wish you all well in the
coming year. I hope those of you who will still be at school next
year will be back to do battle with some good problems in next
year’s Olympiad sequence. If you can find time to reread your
BMO Link Booklet and work on some BMO past papers before the Christmas
holidays, so much the better!
But first make sure your school has entered the NMC on November
22nd 1991. Entry forms may be obtained by sending an SAE to:
NMC, c/o Dulwich College, London SE21 7LD
Any enquiries about the BMO should be addressed to:
Tony Gardiner, Secretary BMOC, School of Mathematics,
University of Birmingham, Birmingham B15 2TT.
Return to IMO Register home page
Contact: Joseph Myers
(imo-register@imo-register.org.uk)
Online HTML version last updated:
5 January 2016
![]()