37th INTERNATIONAL MATHEMATICAL OLYMPIAD
BOMBAY, INDIA
5th-17th JULY 1996
Report by ADAM McBRIDE (UK Team Leader)
Introduction
This report chronicles events leading up to and during this year’s
International Mathematical Olympiad (IMO). As will become clear in
what follows, the IMO was an enormous success mathematically. Never
before at an IMO has every member of a United Kingdom team won either
a gold or a silver medal. Both collectively and individually the team
deserves hearty congratulations. Great credit must also go to the
reserves who made the others fight hard for their places in the team,
as well as to the small band of dedicated colleagues involved in
training the team. It will also become clear that conditions in
Bombay were far from ideal, which makes the team’s success even more
remarkable.
The IMO was the climax of many months of activity throughout the
U.K. involving thousands of mathematically gifted school pupils. The
pupils received the encouragement, guidance and wisdom of a small army
of teachers from the secondary and tertiary sectors, all of them
prepared to give up many hours of their free time for no financial
reward. Individual pupils won certificates, prizes or medals but
perhaps the biggest winner was the subject of Mathematics.
Mathematical Competitions
At this juncture, a short commercial break is in order. In UK
schools we have many youngsters with great mathematical potential.
Some go on to realise their full potential but, alas, many do not. At
the age of 12 or 13, bright pupils are thirsting for knowledge and
relish a challenge. If these pupils are not stretched mathematically,
their fertile minds may turn to other things and be lost to
Mathematics. Mathematical competitions present hard-pressed teachers
with ready-made “extension material” suitable for 30–40% of each
age cohort. There is now a range of such competitions covering all
years in secondary schools. Yet the existence of such competitions is
not well known to many teachers and even less well known to pupils.
Many competition problems require remarkably little mathematical
knowledge but rely for their solution on a little flair and insight.
The satisfaction when the penny drops can be great, while the patience
and determination developed through tackling such problems are
essential attributes for success in life in general. Mathematics is
not a spectator sport. Pupils need to take part and the old Olympic
ideal says that taking part is more important than winning.We can’t
all be winners but we can all learn from the experience.
We have a long way to go before we can match the participation
rates of countries such as Australia. Readers of this report are
probably already in the fold. However, I would ask all readers to
encourage colleagues in neighbouring schools to enter the fray. A
small amount of effort can produce considerable rewards. I should like
to see increased participation from schools in Scotland, Wales and
Northern Ireland. It was unfortunate that there were no girls in the
later stages of this year’s IMO selection process and greater
involvement by the ladies (both pupils and teachers!) should be
encouraged. The younger pupils are when they get involved, the
better. This is where we shall find the seed-corn for mathematicians
of the future.
After that commercial, we are ready to proceed.
Selecting the UK Team
The selection process got under way in November 1995 with the
National Mathematics Contest (NMC) run by the Mathematical
Association. The NMC is a 1½-hour paper containing 25
questions, of which the first 15 are meant to be accessible to most
contestants while the last few are meant to stretch the field. On
this occasion around 33000 pupils took part. Based largely on their
performances in the NMC, around 600 pupils entered the British
Mathematical Olympiad Round 1 (BMO1), a 3½-hour paper with 5
questions held in January 1996. Thereafter 100 pupils were invited to
take BMO2 another 3½-hour paper with just 4 questions, held in
the middle of February. From this group exactly 20 were selected for
a residential Training Session at Trinity College, Cambridge at the
end of March. Selection for this Training Session involved several
criteria. In addition to those expected to be in the IMO team this
year, a number of younger students were blooded as an investment for
the future. The chosen 20 had 4 or 5 intensive 2-hour sessions each
day dealing with Algebra, Combinatorics, Functional Equations,
Geometry, Inequalities and Number Theory. In each session the emphasis
was on tackling problems, with the bare minimum of exposition from the
person leading the session. The whole programme was very successful
and thanks are due to all those who gave so willingly of their time to
prepare material and lead sessions.
The climax of the Trinity Training Session was the Final Selection
Test (FST) held on the last morning. This was a mock IMO-type paper
with just 3 questions to be attempted in 4½ hours. After the
marking of FST, it was time to select the IMO squad in the light of
all the information available. Usually a squad of 7 is chosen and one
of these eventually becomes the non-travelling reserve. This year it
proved impossible to separate a number of people at that stage and so
we ended up with a squad of 8. They were told that they had to fight
for a place in the team of 6 during subsequent weeks. A correspondence
course started in mid-April. The squad received a set of 7 or 8
questions every 10 days, with solutions having to be submitted in
accordance with strict deadlines. Towards the end of May, our
selection was finalised as follows:
| Team: | David Bibby (Ysgol Rhiwabon, Ruabon, North Wales) |
| Michael Ching (Oundle School, Oundle nr. Peterborough) |
| Toby Gee (John of Gaunt School, Trowbridge, Wilts.) |
| John Haslegrave (King Henry VIII School, Coventry) |
| Hugh Robinson (King Henry VIII School, Coventry) |
| Paul Russell (St Bride’s High School, East Kilbride, Scotland) |
| Reserves: | Adrian Sanders (King’s College School, Wimbledon) |
| Bennet Summers (St Paul’s School, London) |
| Team Leader: | Dr Adam McBride (University of Strathclyde, Glasgow) |
| Deputy Leader: | Mr Philip Coggins (Bedford School) |
| Observer: | Dr Gerry Leversha (St Paul’s School). |
(Many countries have Observers at the IMO to allow interested
parties to see what is involved in being either the Leader or Deputy
Leader. On this occasion Gerry shadowed Philip.)
Final Preparations
The correspondence course continued well into June. During the
period 21st to 23rd June, the entire squad gathered at University
College, Oxford in conjunction with the Sharp Summer School being run
there by Tony Gardiner. As well as tackling more problems, we dealt
with travel plans, medical matters and other domestic
arrangements. Another aim was to develop team spirit and allow us all
to get to know each other better. An important cultural interlude
allowed the company to watch England performing in Euro ’96.
The Oxford weekend provided a fitting conclusion to our
preparations. Special thanks are due to Christopher Bradley and Tony
Gardiner for major contributions to the mathematical training and to
Philip Coggins for helping with the correspondence course and for
meticulous attention to details regarding the many items, medical and
otherwise, which we needed to take with us.
The attitude of the squad and the quality of the work produced was
excellent throughout. Great credit goes to all concerned. Particular
mention must be made of our reserves. Adrian and Bennet did indeed
make the others fight very hard for their places and thereby
contributed substantially to the UK cause. Both remained fully
involved throughout and they will be ready to enter the fray again
next year. Bennet was responsible for designing the UK T-shirt, a
rather nice blue creation which was remarked on most favourably by
many people in Bombay. “The boys in blue” certainly stood out from
the crowd.
Timetable of the 37th IMO
The Jury, comprising the Team Leaders of all competing countries,
met for the first time on 6th July and spent the next three days
selecting the problems for the two papers and approving the
translation of the papers into all the required languages (43 in
all). The Team, Deputy Leader and Observer arrived on 8th July and the
Official Opening Ceremony was held the next day. The two examination
papers were scheduled to take place between 9 a.m. and 1.30 p.m. on
10th and 11th July. Thereafter the contestants could relax while
Leaders and Deputy Leaders embarked on marking and
co-ordination. Three days were allocated for this but only two were
needed. There was a gymnastic display followed by a banquet on 15th
July and the Closing Ceremony, including the presentation of medals,
took place the following day.
The Problems
All contestants sat two papers on consecutive days. Each paper
contained three questions, each question being worth 7 points.
On each day the time allowed was 4½ hours.
The questions were proposed by the countries indicated.
FIRST DAY
-
Let ABCD be a rectangular board with |AB| = 20,
|BC| = 12. The board is divided into 20 × 12 unit
squares.
Let r be a given positive integer.
A coin can be moved from one square to another if and only if
the distance between the centres of the two squares is 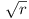 .
.
The task is to find a sequence of moves taking the coin from
the square which has A as a vertex to the square which has
B as a vertex.
- Show that the task cannot be done if r is divisible
by 2 or 3.
- Prove that the task can be done if r = 73.
- Can the task be done when r = 97?
(Finland)
-
Let P be a point inside triangle ABC such that
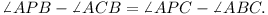
Let D and E be the incentres of triangles
APB and APC respectively.
Show that AP, BD and CE meet at a point.
(Canada)
-
Let S = { 0, 1, 2, 3, ... } be the set of non-negative
integers. Find all functions f defined on S and
taking their values in S such that
f(m + f(n)) =
f(f(m)) + f(n) for all
m, n in S.
(Romania)
SECOND DAY
-
The positive integers a and b are such that the
numbers 15a + 16b and 16a - 15b are
both squares of positive integers.
Find the least possible value that can be taken by the minimum
of these two squares.
(Russia)
-
Let ABCDEF be a convex hexagon such that AB is
parallel to ED, BC is parallel to FE and
CD is parallel to AF.
Let RA, RC
and RE denote the circumradii of
triangles FAB, BCD and DEF respectively.
Let p denote the perimeter of the hexagon.
Prove that
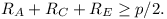
(Armenia)
-
Let n, p and q be positive integers with
n > p + q.
Let x0, x1, ...,
xn be integers satisfying the following
conditions:
- x0 = xn = 0
- for each integer i with
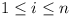 ,
,
either xi -
xi-1 = p or
xi - xi-1 =
-q.
Show that there exists a pair (i, j) of indices
with i < j and 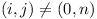 such that
xi = xj.
such that
xi = xj.
(France)
You are invited to send in solutions, enclosing an SAE please, to:
Adam McBride, Department of Mathematics
University of Strathclyde, Livingstone Tower,
26 Richmond Street, GLASGOW G1 1XH.
How the UK Team Performed
A total of 424 contestants from 75 countries took part.
The UK team finished 5th out of 75 with 161 points (out of 252).
Each of the 6 team members won a medal, the haul being
2 Gold Medals and 4 Silver Medals.
Individual scores were as follows:
| Q1 | Q2 | Q3 | Q4 | Q5 | Q6 | Total | |
|---|
| David Bibby | 7 | 5 | 7 | 7 | 0 | 7 | 33 | Gold |
| Michael Ching | 7 | 0 | 7 | 7 | 0 | 7 | 28 | Gold |
| Toby Gee | 4 | 7 | 6 | 7 | 2 | 1 | 27 | Silver |
| John Haslegrave | 7 | 0 | 7 | 4 | 1 | 7 | 26 | Silver |
| Hugh Robinson | 7 | 1 | 3 | 7 | 1 | 7 | 26 | Silver |
| Paul Russell | 7 | 1 | 5 | 7 | 0 | 1 | 21 | Silver |
David Bibby was 14th equal and Michael Ching was 33rd equal (out of
424).
The top ten teams were
| Romania 187 | United States 185 | Hungary 167 | Russia 162 |
| United Kingdom 161 | China 160 | Vietnam 155 |
| Republic of Korea 151 | Iran 143 | Germany 137. |
The IMO is a competition for individuals. Officially there is no
team competition, but unofficially great interest attaches to the team
totals. In this respect, our achievement in coming 5th is
remarkable. All the other countries listed above invest considerable
sums of money in the training of their teams. Training camps lasting
for weeks and months rather than days are common. By comparison, our
operation runs on a shoestring. Although we are thoroughly
professional in the mathematical sense, we remain amateurs in the
sense of the true Olympic ideals. Looked at in this light, our
performance can be regarded as a triumph of a David (and Hugh, John,
Michael, Paul and Toby!) over Goliaths.
Overall Performance of All Contestants
The papers proved to be tough. Only one contestant (from Romania)
scored the maximum of 42. No one scored 41 or 40, one contestant
scored 39 and another 38. The range of scores for the various medals
was:
| Gold | From 28 to 42 | (35 contestants) |
| Silver | From 20 to 27 | (66 contestants) |
| Bronze | From 12 to 19 | (100 contestants). |
It is worth commenting on Q5. Of the 424 contestants no fewer than
308 scored 0 on this question and the average score (out of 7) was
0.49! That makes our team total of 4 almost respectable. Geometry is
found hard by students from all countries. (Various reasons could be
put forward!) Interestingly enough, of the 104 problems submitted in
advance for possible use in the competition, 43 were on geometry. This
total included two composed by Dr David Monk (formerly of the
University of Edinburgh) and one by Dr Christopher Bradley (Clifton
College, Bristol), all three of which made the short list but none of
which was eventually used.
Organisation of the 37th IMO
It must be said that conditions in Bombay were far from ideal. It
must also be said that the local organisers did a marvellous job. The
problems which arose were outwith their control and they spared no
effort to minimise the inconvenience.
Originally the IMO was to take place in New Delhi and plans were
well advanced at that venue. However, it appears that six different
government agencies were competing to run the show and a total
bureaucratic stalemate ensued. Eventually it was decided that the IMO
would move to Bombay, where there was only one relevant agency to deal
with. The decision was taken in mid-March and left the locals with
104 days to get their show on the road, starting completely from
scratch. That they succeeded was little short of a miracle. They had
to make do with whatever accommodation could be found and that for the
contestants was extremely basic (to put it mildly). The Leaders were
25 miles out of town. This meant frequent long bus journeys, courtesy
of a shambolic bus company which was likely to go bankrupt at any
minute. Then there was the monsoon which produces much more rain in
Bombay than in New Delhi. Finally the ambience of Bombay was
dreadful. Most of the city is a gigantic slum with abject poverty and
appalling squalor all too visible. Yet despite everything (including
many instances of upset stomachs, sickness and diarrhoea), we survived
to tell the tale of an unforgettable IMO.
All decisions concerning the competition were in the hands of the
Jury which consisted of the 75 Team Leaders, each of whom had one
vote. We were each supplied with a thin plastic object shaped like a
table-tennis bat with our own 3-letter code marked on it. The UK code
was UNK so that I was “The Man from UNK”! Votes were frequent and
consisted of the chairman counting the number of raised bats. The
flexible nature of the bats meant that they also served as
much-needed fans. The business of the Jury was conducted mainly in
English but Russian translations were supplied when needed. Our main
tasks were to select the problems for the paper, approve the various
translations, confirm the marks scored, award medals and deal with any
other matters related to the IMO regulations. We were fortunate to
have Professor A M Vaidya (Chairman) and Dr S Shirali (Convener of the
Problems Committee) to get us through our business in a relaxed but
highly efficient way.
The other major task for the Leaders and Deputy Leaders was the
marking of the scripts. We each marked the scripts of our own team and
then had to justify our marking before a panel of
Co-ordinators. Despite occasional disputes which had to go to
arbitration, the process was completed a day ahead of schedule. Behind
the scenes a team led by Dr S P Arya produced regular computerised
updates of the marks scored. All concerned deserve great praise for
their efficiency and their unfailing courtesy.
Daily Diary
A picture of how the IMO unfolded can perhaps be conveyed best via
a brief summary of what happened every day, as seen through my eyes.
5 July Leave home at 05.30 to catch the shuttle to London.
Arrive in Bombay at 23.45 local time with the thermometer registering
84°F. Long queues at immigration. Lots of officials standing
around doing nothing. Outside chaos reigns. All 42000 taxi drivers are
on strike over a hike in the price of petrol. All autorickshaws are
also at a standstill. Fortunately I am being picked up by IMO
staff. It is now 01.00 but the streets are full of people and
dogs. Drive to hotel takes an hour and gives me my first sight of the
slums. Our 5-star hotel is on the shores of the Arabian Sea. To bed at
02.30.
6 July After breakfast, collect the short-listed problems
and solutions. Also collect a nice brief-case, an umbrella and two
T-shirts, all specially customised with the IMO logo. First jury
meeting adjourned after an hour to allow us to try more of the
problems. Pattern continues throughout the day. By evening 7 out of 30
problems on the short list have been discarded. After dinner, work
through 9 geometry problems, including 3 of our own.
7 July A long day. Spend 5 hours finalising the paper via a
convoluted sequence of votes, at least two of which seem mutually
contradictory. It is suggested that we then prepare the version in
English. I suggest that it is crazy to do this in a meeting of 75
people and ask for an adjournment. The English-speaking Leaders do
some surgery on Q1 and bring back two versions. There is an argument
over using “20 × 12” versus “240”! 20 × 12 wins.
8 July First we agree the versions of the paper in French,
German, Russian and Spanish. Then comes business of the IMO Advisory
Board, the body responsible for planning future IMO’s. We hear that
the USA will host the IMO in 2001. We discuss an IMO logo and the
rules for elections to IMOAB. In the elections the successful
candidates are the Leaders of Turkey and Hungary (the latter described
in The Times of India as the Jesse Owens of Mathematics because
of all the medals he won as a competitor many years ago.) Next we
peruse all the other translations of the paper prepared by Leaders. I
spot errors in the versions in Estonian, Icelandic and Swedish (easier
than you might think, even if you don’t understand all the words!)
9 July Quiet morning then off to the Opening Ceremony.
Journey there and back takes 2 hours along congested, poorly
maintained roads. The people and dogs are now augmented by cattle and
the odd buffalo or elephant. Drivers are crazy; horn first, brake
second! Ceremony starts with some speeches. I see Philip, Gerry and
the team from the balcony. (The Leaders now know the contents of the
papers and are segregated from the teams.) My UK T-shirt designed by
Bennet is thrown up to me. After speeches, a long pause. The punters
get restive. Eventually we have a display of classical Indian
dancing, including a special choreographed version of an old Indian
mathematical problem related to the theorem of Pythagoras. Meet a
representative of the British Deputy High Commission, a useful
contact. BBC are there too apparently but we fail to rendezvous. Back
to base, to the accompaniment of an over-loud Dustin Hoffman video.
10 July First day of the competition. Breakfast at 06.30
before our usual 2-hour bus ride (videos now barred after a mutiny!).
Arrive at exam hall in Bombay Atomic Research Centre
(BARC). Mathematics seems to belong to the Department of Atomic
Energy! During the first hour of the 4½-hour paper, students
can send written queries by messenger to the Jury. These are answered
in strict rotation and written replies taken back to the
students. Today we get 21 queries. After a welcome cup of tea, some
brave souls set off to see the city centre. I return to base for a
quiet afternoon. Send a FAX of congratulations to my students at
Strathclyde who are graduating that day. Thoughts turn to
home. Reverie broken by arrival of scripts from morning exam. Quick
glance suggests Q1, Q3 are solid, Q2 distinctly dodgy. Mark Q2 after
dinner. Think of marking Q1. Go to bed instead.
11 July Second day of the competition. Jury receives 51
queries, mainly seeking clarification about the meaning of minimum
when applied to two equal numbers. Leaders supposed to go on a bus
trip to Lonavala, 108 kms south of Bombay. I opt to stay at the BARC
campus. Meet up with Philip and Gerry. Inspect the student
accommodation. Fairly primitive. Meet team after exam. (This is the
first time I’ve been able to speak to them since we left the U.K.!)
Over lunch it becomes clear that Q5 is a disaster all round but the
lads seem happy with their performance otherwise. Encourage team to
socialise with other teams now that the hard work is over. Will be
difficult given the surroundings. Philip and Gerry move to my hotel
for the rest of the proceedings. Team left at BARC with their guide, a
local postgraduate student. I feel for them. Chaos at the hotel as
some Deputy Leaders are in a separate hotel from their leaders (3 km
apart). Philip shares a room with me. Gerry finds himself sharing
with the Portuguese Leader! The key for our room snaps in my hand! A
replacement is sought. The scripts arrive and we get stuck into them
after dinner. The heavens open and thunder rolls. Ahead lie two days
without a bus ride. Bliss!
12 July First day of co-ordination. Hard work but
successful beyond our wildest dreams. Off to a flying start with Q2,
getting more marks than we expected. Q6 epitomises the team
spirit. Michael’s solution is beautifully clear and gets 7
easily. Paul and David have used similar methods to Michael and,
although we have to work harder, a virtuoso performance by Philip gets
7 for both. The other three solutions involve different approaches but
we are on a roll and wrap up a total of 30. Earlier Q4 proved a
block-buster with a total of 39 out of 42. Telephone system is such
that we can’t contact team but they can contact us. They phone around
7 p.m. to find out about Q6. (The marks for Q2, Q4 have already got
down to BARC.) I can hear Toby but he can hardly hear me but we get
there. We have 83 points at the end of the day. Looks like a top 10
finish and medals for everyone (but of what kind?). Things are getting
very exciting. After dinner mark Q1, another cracking
performance. Confirm Q5 is a disaster. Any marks at all will be a
bonus. Q3 looks good. Get our replacement key. Retire to bed. Don’t
sleep well. Too pumped up.
13 July A truly wonderful day. From 09.30–11.00 work on
Q3. Aim for at least 30. Supposed to co-ordinate Q1 at 11.00 but
things are behind schedule. Get going at 12.10. Goes very well. After
lunch Q3 is hard work but suddenly all the lights go out. Total
darkness loosens everyone up and we get 35. Great! That leaves Q5. We
get 4, which is 4 more than China. Unbelievable! Excitement is now at
fever pitch. As more and more scores go up on the boards, things look
better and better. The Australian leader and I do rapid calculations
to predict cut-offs for medals. By dinner, we are heading for 6th
place and the worst case scenario for medals is 1 Gold and 5
Silver. Will we get another Gold? It looks as if Michael will just
squeeze in. At dinner, the Irish Deputy Leader comes over to tell us
that China have done badly on Q6 and that we have beaten them by one
point. We are 5th! The team phone. Struggling to make myself heard, I
give them the predictions which seem certain to be confirmed at the
final Jury meeting. What a triumph! Relax with other Leaders and
Deputy Leaders. Reports of several tummy bugs and one or two people
are really quite ill. I’m feeling pretty good! Receive
congratulations from many other countries. Despite the fierce
competition, the IMO engenders great sportsmanship and friendliness.
All countries exchange gifts such as pens, key-rings, books of
problems, even coffee from Colombia. A truly wonderful day. Can’t
sleep. Even more pumped up.
14 July A bus is supposed to turn up at 09.30 to take people
shopping. It hasn’t appeared by 11.00 and most abandon the trip. The
afternoon sees people relaxing (in the pool and jacuzzi, playing
bridge and snooker). I tell the team they are welcome to come up to
our hotel but the thought of a 2-hour journey each way persuades them
to stay at BARC. Final Jury meeting is shortest on record. Results
confirmed. Several votes of thanks to the chairman, the Problems
Committee and the staff of the IMO Office for making the 37th IMO such
a mathematical success.
15 July Nothing scheduled until 16.00 downtown. Spend
morning writing postcards, sending a FAX to Tony Gardiner at ICME in
Seville and issuing a News Release via the British Deputy High
Commission. Philip, Gerry and I decide to head off at noon, catch a
train and find out if there is another side to Bombay. Take taxi to
Malad station (7 miles, around £4). Get a train to Churchgate
(21 miles but costing only 15 pence!). Indian trains
are chaotic. All the doors are open and people are hanging on to the
outside. We stand most of the way, manage to avoid falling out and
enjoy the ride. We go looking for shops but fail miserably only
finding a political demonstration and the thrill-a-minute World Trade
Centre. Take taxi to Homi Bhabha Auditorium. Meet the team as they
arrive. Haven’t seem them for four days. Congratulate each of them
individually. We are treated to a spectacular display of Mallakhamb,
a form of gymnastics centred on a pole 260 cms high with a
circumference of 55 cms at the base tapering to 20 cms at the top.
Mallakhamb is claimed to be “a scientific and systematic method of
acquiring a sound body and mind.” The performers are a dozen girls
whose ages and heights are in arithmetic progression (6 years to 18
years and 4 feet to 6 feet) and an isomorphic group of boys. The
exercises on the pole get more and more daring and culminate in human
pyramids in which people hold on to the pole with their toes. The
performance is greeted with enormous enthusiasm by everyone. A magic
show follows but this is a total anti-climax. We then adjourn to a
posh hotel for a “banquet” (in reality a stand-around buffet). At
last everybody involved in IMO (contestants, guides, co-ordinators,
Leaders and Deputy Leaders) can get together socially and a carnival
atmosphere develops. The Irish Deputy Leader (from Aberdeen) leads the
company in a rendition of “Cockles and Mussels”, to be followed by
various other teams, notably the Colombians and the Indians. All too
soon the dreaded buses arrive to take us back to base. Hope the party
will continue at BARC.
16 July Transport to the Closing Ceremony is a
shambles. Things get under way late. Even then at least one of the
platform party is stranded somewhere in a bus. The lads receive their
medals one by one. I try to capture each presentation on
film. Speeches follow. Then group photos on the stage with all of us
sporting our blue T-shirts. “The boys in blue” create quite an
impression. We abandon the dancing that follows in favour of setting
off for BARC. Horrendous journey lasting 2½ hours through
colossal traffic jams. Reach BARC around 21.15. Grab a quick bite then
catch the first available bus to the airport. All day long the rain
pours down.
17 July Reach airport just after midnight. Have 3½
hours to kill but we are no longer at the mercy of the bus
company. Take off at 03.45, stop off at Delhi around 06.00, land at
Heathrow at 11.30. Meet some of the parents. Go our separate
ways. Home at 15.00 for a drink of nice cool tap water, a square meal
and 13 hours of sleep.
Concluding Remarks
That was IMO96, an unforgettable experience. It only remains to thank
- all the pupils who took part at any stage
- all the teachers who encouraged the pupils and supported our
endeavours
- Peter Neumann for skilfully guiding the British Mathematical
Olympiad Committee at a time of change
- the Problems Group, especially Christopher Bradley and David
Monk, for creating so many interesting problems
- Alan West and Brian Wilson, organisers of BMO1 and BMO2
respectively
- all those who helped with the marking of BMO1
- all those who contributed to the Trinity Training Session,
particularly Christine Elliott for her excellent organisation
- all our sponsors, especially Trinity College, Cambridge for
hosting the March training session and the Royal Society for
hosting the September celebration
- DfEE for a grant covering travel to and from Bombay
- Tim Cross for producing the 1996 BMO booklet, copies of which
are now all over the world
- Tony Gardiner for his myriad contributions
- Philip Coggins for assistance with the correspondence course
and, along with Gerry Leversha, for help of all sorts before and
during the visit to India.
Finally, let us congratulate the squad of 8 for a magnificent
effort and the team of 6 for producing an outstanding performance and
for being excellent ambassadors for the United Kingdom. They did us
proud and it was a great honour and a great pleasure for me to be
their Leader.
imo/aw/24.7.96
Return to IMO Register home page
Contact: Joseph Myers
(imo-register@imo-register.org.uk)
Online HTML version last updated:
5 January 2016
![]() .
.![]()