38TH INTERNATIONAL MATHEMATICAL OLYMPIAD
MAR DEL PLATA, ARGENTINA
18-31 July 1997
Report by ADAM McBRIDE (UK Team Leader)
Introduction
This report chronicles events leading up to and during this year’s
International Mathematical Olympiad (IMO). The 38th IMO was notable
for a variety of reasons. For example, 82 countries took part, the
highest number ever. The organisation was superb from start to
finish. Accommodation for the teams was good, with lots of facilities
in the hotel to let students from all over the world socialise and get
to know each other. The hotel for the Team Leaders (plus Deputy
Leaders and Observers who moved there after the second paper) was
palatial. The weather was extremely pleasant and the general ambience
excellent.
On the mathematical front, it is probably fair to say that the
problems chosen for the competition did not play to the strengths of
the UK team this year and did not allow them to display fully their
outstanding ability. Nevertheless, there was much to be proud of.
Throughout the months of training, the attitude of the whole squad,
including our reserve, was first-rate. All of us were under
considerable pressure but the show stayed on the road. It was a
privilege and a pleasure to work with the squad and to lead the team
to Argentina. I congratulate all the students on their achievements.
Of course, the IMO represents just the apex of a very large
pyramid. During the entire selection procedure, which is discussed in
more detail below, thousands of pupils took part, supported and
encouraged by hundreds of teachers throughout the country. Thanks
must go to all of them. Not everyone can win a place in an IMO team
but, in the spirit of the original Olympic Games, taking part is what
matters. I hope that in 1997/98 the number of participants will
continue to increase. As I mentioned in last year’s report, we need
more representation from schools in Scotland, Wales and Northern
Ireland, while the number of girls involved in the later stages was
again extremely disappointing. Let us see if this can be rectified
next year.
Mathematical Competitions in the UK
During the last year significant changes have been taking place in
the organisation of a number of the UK-wide mathematical competitions.
It seems appropriate to describe some of these changes here.
(However, those of a tender disposition may wish to proceed to the
next section!)
For many years the Mathematical Association has run the National
Mathematics Contest (NMC) aimed at senior pupils. The NMC has acted
as the gateway to Rounds 1 and 2 of the British Mathematical Olympiad
(commonly called BMO 1 and BMO 2) and ultimately to the IMO. During
the last ten years, thanks to the enthusiasm and hard work of Dr.Tony
Gardiner (University of Birmingham), the UK Junior Mathematical
Challenge (UKJMC) and UK Intermediate Mathematical Challenge (UKIMC)
have been established to cater for students in earlier years of
secondary education. Both the latter competitions have follow-up
activities for which pupils are selected on the basis of their
performance in the first stage. These activities include the UK
Junior Mathematical Olympiad (UKJMO), the International Intermediate
Invitational Mathematical Challenge (IIIMC) and the European Kangaroo.
A new body called the United Kingdom Mathematics Trust (UKMT) has
been set up to co-ordinate the organisation of all the competitions
mentioned above. Most of the day-to-day running of the competitions
will be done by four subtrusts. One subtrust will deal with the UKJMC
and UKIMC, while a second subtrust will look after the UKJMO, IIIMC
and Kangaroo. At the senior level, the Senior Challenges Subtrust
(SCS) will be responsible for the UK Senior Mathematical Challenge
(UKSMC), which is the new name for the NMC. Finally, the Senior
Olympiad Subtrust (SOS) will be responsible for everything from BMO 1
through to the IMO. To preserve some measure of continuity, the
familiar title of British Mathematical Olympiad Committee (BMOC) will
be retained for use by the SOS.
At this stage the reader could be forgiven for being totally
bamboozled by all the acronyms. (The use of SMC is particularly
confusing because it also stands for Scottish Mathematical Council, a
venerable body which has run its own Mathematical Challenge for over
20 years. The latter competition, which complements the others
because of its different format, remains under the sole control of the
Scottish Mathematical Council.) Membership of the various subtrusts
is now almost complete and the new system should be fully operational
in 1997/98. For information, the Chairman of the UKMT is Dr. Peter
Neumann (Queen’s College, Oxford), the Chairman of the SCS is Mr. Bill
Richardson (Elgin Academy) and the Chairman of the BMOC (SOS) is
Prof. Jim Wiegold (University of Wales, Cardiff). With a group of new
enthusiastic recruits joining some of the seasoned campaigners, the
new structure should relieve the pressure on individuals and ensure
the long-term future of all the competitions.
Now we can get back to our main business.
Selecting the UK IMO Team
As usual the process began in November 1996 with the UKSMC. The
name may have changed from NMC but the format was the same. The
1½-hour paper contained 25 multiple-choice questions, the first
15 meant to be accessible to most contestants and the remainder
designed to stretch the field. Around 35000 pupils took part. Based
largely on their performances in the UKSMC, over 700 pupils entered
BMO 1, a 3½-hour paper with 5 questions held in mid-January.
Thereafter, 100 pupils were invited to take part in BMO 2, another
3½-hour paper with just 4 questions, held at the end of
February. From this group, exactly 20 were selected for a residential
Training Session at Trinity College, Cambridge in April. Selection
for this Training Session was based on several criteria. In addition
to the strongest contenders for this year’s IMO team, some younger
students were blooded as an investment for the future. The chosen 20
had 4 or 5 intensive 2-hour sessions each day dealing with Algebra,
Combinatorics, Functional Equations, Geometry, Inequalities and Number
Theory. In each session the emphasis was on tackling problems, with
the bare minimum of exposition from the person leading the session.
Thanks are due to all who gave so willingly of their time to prepare
material and lead sessions. We were specially pleased to have with us
Professor Derek Holton (University of Otago), a regular Leader of the
New Zealand IMO team and well known in this country through his series
of problem-solving booklets. (During our stay in Cambridge, the
weather was glorious. Walking through the Fellows’ Garden each
morning on the way to breakfast was a delight, as was punting on the
Cam. Courtesy of Bill Richardson we also had a trip to the
Observatory to look at the Hale-Bopp comet.)
The climax of the Trinity Training Session was the Final Selection
Test (FST). There may be more relaxing ways of spending 4½
hours on a Sunday morning under a cloudless sky but duty calls. The
mock IMO paper contained just 3 questions. When the students had
gone, a group of 6 staff stayed on to mark FST, after which the IMO
squad of 7 was selected. The 7 students then embarked on a
correspondence course. They received sets of 8-10 problems every 10
days and were required to submit solutions in accordance with strict
deadlines. Towards the end of May, our selection was finalised as
follows:
| Team: | Mansur Boase (St. Paul’s School, London) |
| Michael Ching (Oundle School, Oundle nr. Peterborough) |
| Toby Gee (John of Gaunt School, Trowbridge, Wilts.) |
| Adrian Sanders (King’s College School, Wimbledon) |
| Amit Shah (Haberdashers’ Aske’s School, Elstree) |
| Bennet Summers (St. Paul’s School, London) |
| Reserve: | Colin Phipps (Bristol Grammar School) |
| Team Leader: | Adam McBride (University of Strathclyde, Glasgow) |
| Deputy Leader: | Philip Coggins (Bedford School) |
| Observer: | Michael Davies (Westminster School) |
Of the team, Michael and Toby went to Bombay in 1996 while Adrian
and Bennet were last year’s reserves. Sending an Observer to the IMO
allows interested parties to see what is involved in being either the
Leader or the Deputy Leader. On this occasion Michael Davies shadowed
Philip.
Final Preparations
The correspondence course continued until the beginning of July,
with occasional interruptions because of A-levels and other exams.
During the period 2-6 July, the whole squad gathered at Queen’s
College, Birmingham in conjunction with the Summer School being run
there by Tony Gardiner. As well as tackling more hard problems,
including another mock IMO paper, the squad were able to get to know
each other better and to develop team spirit. Cultural interludes
were provided by a walk along the canal to see a performance of “The
Importance of Being Earnest” and a “Mathematical Mélange” in
which the younger students at the Summer School displayed their
musical, dramatic and juggling abilities to a remarkably high
standard. The Summer School was enormously successful and we are all
most grateful to Tony Gardiner for the huge amount of work he put in
to get it organised.
The Birmingham Summer School provided a fitting conclusion to our
preparations. I am particularly grateful to Christopher Bradley for
his major contribution to the mathematical training, especially in
geometry, and to Philip Coggins for helping with the correspondence
course, for meticulous care in arranging flights and for dealing with
all manner of domestic and medical matters relevant to our trip.
As previously mentioned, the attitude of the squad was excellent
throughout. Special thanks to our reserve, Colin Phipps, who stayed
fully involved right up to departure and contributed to the team
effort by making the others fight every inch of the way.
Timetable of the 38th IMO
The Jury, comprising the Team Leaders of all competing countries,
met for the first time on 19 July and spent the next three days
selecting the problems for the two papers and approving the
translation of the papers into all the required languages (48 in all).
The Team, Deputy Leader and Observer arrived on 21 July and the
Opening Ceremony was held on 23 July. The two examination papers took
place between 08.30 and 13.00 on 24 and 25 July. Thereafter the
contestants could relax and go on excursions while the Leaders and
Deputy Leaders embarked on marking and co-ordination, lasting three
days. The Closing Ceremony, including the presentation of medals,
took place on 30 July.
The Problems
All contestants sat two papers on consecutive days. Each paper
contained three problems, each problem being worth 7 points.
On each day the time allowed was 4½ hours.
The problems were proposed by the countries indicated.
FIRST DAY
-
In the plane the points with integer co-ordinates are the
vertices of unit squares. The squares are coloured alternately
black and white (as on a chessboard).
For any pair of positive integers m and n,
consider a right-angled triangle whose vertices have integer
co-ordinates and whose legs, of lengths m and n, lie
along edges of the squares.
Let S1 be the total area of the black part of
the triangle and S2 be the total area of the
white part. Let
f(m, n) =
|S1 - S2| .
- Calculate f(m, n) for all positive
integers m and n which are either both even or
both odd.
- Prove that
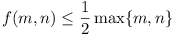 for all m and
n.
for all m and
n.
- Show that there is no constant C such that
f(m, n) < C for all
m and n .
(Belarus)
-
Angle A is the smallest in the triangle ABC.
The points B and C divide the circumcircle of the
triangle into two arcs. Let U be an interior point of the
arc between B and C which does not contain A.
The perpendicular bisectors of AB and AC meet the
line AU at V and W, respectively. The lines
BV and CW meet at T.
Show that
AU = TB + TC .
(United Kingdom)
-
Let x1, x2, ...,
xn be real numbers satisfying the
conditions
|x1 + x2 +
... + xn| = 1
and 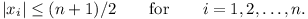
Show that there exists a permutation y1,
y2, ..., yn of
x1, x2, ...,
xn such that
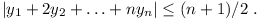
(Russia)
SECOND DAY
-
An n × n matrix whose entries come from the
set S = { 1, 2, ..., 2n - 1 } is called a
silver matrix if, for each i = 1, ..., n, the
ith row and ith column
together contain all the elements of S. Show that
- there is no silver matrix for n = 1997;
- silver matrices exist for infinitely many values of n.
(Iran)
-
Find all pairs (a, b) of positive integers
a and b that satisfy the equation
ab2 =
ba .
(Czech Republic)
-
For each positive integer n, let f(n)
denote the number of ways of representing n as a sum of
powers of 2 with non-negative integer exponents.
Representations which differ only in the order of their
summands are considered to be the same. For instance, f(4)
= 4 because the number 4 can be represented in the following four
ways:
4 ; 2 + 2 ; 2 +
1 + 1 ; 1 + 1 + 1 + 1 .
Prove that, for any integer 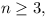
2n2 / 4 <
f(2n) < 2n2 / 2 .
(Lithuania)
You are invited to send in solutions, enclosing an SAE please,
to:
Adam McBride, Department of Mathematics,
University of Strathclyde, Livingstone Tower,
26 Richmond Street, GLASGOW G1 1XH.
Comments on the Problems
Participating countries submitted over 150 problems, with geometry
the most popular area. The organisers produced a short list of 26
problems for consideration by the jury. The United Kingdom submitted
6 problems, of which 3 were included in the short list. One of these,
composed by David Monk (formerly University of Edinburgh) was chosen
as the second problem on the first day. Another of David’s problems
was short-listed, as was one by Christopher Bradley (Clifton College,
Bristol). Christopher and David must be two of the most prolific and
imaginative composers of problems in the world, both having a keen
interest in geometry. It is fitting that we should congratulate
Christopher on being declared 1996 Problem Solver of the Year by the
journal Crux Mathematicorum. We look forward to many more
ingenious problems from both Christopher and David in the future.
As regards Problem 4, there was much discussion about what to call
a matrix with the stated property. The word “silver” was mentioned
as a joke. (Remember where the IMO was being held!) It is fair to
say that not all countries were happy with “silver” but it was voted
through.
How the UK Team Performed
A total of 460 contestants from 82 countries took part.
The UK team finished 16th out of 82 with 144 points (out of 252).
Team members won
1 Gold Medal, 2 Silver Medals and 2 Bronze Medals.
Individual scores were as follows:
| Q1 | Q2 | Q3 | Q4 | Q5 | Q6 | Total | |
|---|
| Mansur Boase | 0 | 7 | 6 | 7 | 3 | 5 | 28 | Silver |
| Michael Ching | 4 | 7 | 0 | 7 | 7 | 0 | 25 | Silver |
| Toby Gee | 0 | 7 | 1 | 5 | 4 | 1 | 18 | Bronze |
| Adrian Sanders | 4 | 7 | 0 | 7 | 0 | 3 | 21 | Bronze |
| Amit Shah | 4 | 0 | 0 | 4 | 6 | 0 | 14 | |
| Bennet Summers | 7 | 7 | 7 | 7 | 7 | 3 | 38 | Gold |
Bennet’s score put him 15th equal. Amit was unlucky to miss a
bronze medal by just one mark.
The papers contained quite a lot of things that could be classed as
combinatorics. Problem 1, which was meant to be a reasonably
accessible question, was found hard by the UK team (and many others).
Given the large number of geometry problems proposed, it seems
surprising that only one saw the light of day. Another geometry
problem on the second day might have suited us better, as might a
functional equation.
Overall Performance of All Contestants
There was a conscious effort to make the papers somewhat easier
than last year (when scores of 28, 20 and 12 were the lower cut-offs
for gold, silver and bronze, respectively). The outcome was
satisfactory. The ranges of scores for the various medals were:
| Gold | From 35 to 42 | (39 contestants) |
| Silver | From 25 to 34 | (70 contestants) |
| Bronze | From 15 to 24 | (122 contestants). |
Four students scored full marks. Alas, 15 students scored 0.
(These students came largely from Latin/South American countries
competing for the first time.)
For the statistically minded, the individual problems produced the
following means (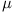 )
and standard deviations (
)
and standard deviations (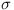 ):
):
| Q1 | Q2 | Q3 | Q4 | Q5 | Q6 |
|---|
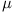 | 2.48 | 3.89 | 1.78 | 3.74 | 3.35 | 0.82 |
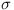 | 2.23 | 3.31 | 2.75 | 2.72 | 2.97 | 1.72 |
Although the IMO is an individual competition and, officially,
there is no team competition, considerable interest still attaches to
team totals. For the record, here are the top 16:
| 223 China | 219 Hungary | 217 Iran |
| 202 Russia, USA | 195 Ukraine | 191 Bulgaria, Romania |
| 187 Australia | 183 Vietnam | 164 South Korea |
| 163 Japan | 161 Germany | 148 Taiwan |
| 146 India | 144 United Kingdom. |
Interested readers can make what they will of all these statistics.
The rest of us will move on.
Organisation of the 38th IMO
This IMO will be remembered as one of the best ever from the point
of view of organisation. A team of professionals had been engaged to
deal with all the preliminary planning (e.g. submission of problems,
names of contestants, flight details, transport requirements). These
ladies were on hand throughout the proceedings and cheerfully helped
to sort out any difficulties that arose. Transport was meticulously
planned, buses turned up at the right time and checks were made to
make sure that nobody got left behind. Staff were present at both
airports in Buenos Aires and at the airport in Mar del Plata to meet
flights and arrange transfers. Each team was allocated a guide, a
local student who could speak the appropriate language and made sure,
among other things, that nobody slept in on the morning of the exams.
Reference was made earlier to the standard of accommodation.
Although students were three to a room, the quality of the rooms was
more than adequate. Various facilities, including a games room and a
computer room, had been laid on and there was ample opportunity for
students to socialise. At the Leaders’ 5-star hotel, luxury was the
name of the game. Apart from rooms for formal meetings, other rooms
were available for working or relaxing, all with a constant supply of
tea, coffee, bottled water and small cakes. A particular favourite
was a room right on the top with a panoramic view over the sea. At
both hotels, the ambience was conducive to making the 38th IMO a very
friendly affair.
All decisions concerning the actual competition were in the hands
of the Jury which comprised the 82 Team Leaders, each of whom had one
vote. We each had a plastic wand with our own 3-letter code marked on
it. The UK code was UNK so that, as usual, I was “The Man from
UNK”! Votes came thick and fast and majorities were based on the
number of wands raised. The business of the Jury was conducted in
English, with occasional translations into other languages when
required. The first three days were taken up with the selection of
the problems and preparation of examination papers in nearly 50
languages. This is a complicated business at the best of times and
firm control is needed to avoid things turning into a shambles. Our
chairman during this period had no previous experience of an IMO. As
a result, the selection of problems took a few bizarre twists.
Sometimes we seemed to be voting for individual problems, sometimes
for pairs of problems and sometimes for triples to form an entire
paper. Around noon on the second day, things were decidedly squiffy.
However, by mid-afternoon, the selection process was complete.
Subsequent jury meetings were chaired by Carlos Bosch, an IMO stalwart
with a sure touch who ensured that things went swimmingly.
The other major task for Leaders and Deputy Leaders was the marking
of scripts and co-ordination of the marks. We each marked our own
team’s scripts and then had to justify our marks before a panel of
co-ordinators. It was up to Philip Coggins, Michael Davies and myself
to get as many marks as possible for our students on the basis of the
scripts which had been presented to us. The three of us worked
splendidly as a team and I should like to thank Philip and Michael for
all their hard work and for their ability to explain a complicated
solution in a highly convincing way. After the exam, the organisers
had photocopied every sheet of paper submitted by every student. This
enabled co-ordinators to read scripts in advance and get a feel for
the various methods of solution used by students. The considerable
time and cost involved in photocopying every sheet was amply
justified. Co-ordination, which is always an intense business, went
smoothly. Discussions were amicable and justice was done. The
co-ordinators, who numbered well over 40 and came from all over the
world, deserve our thanks for all their labours. As soon as a set of
marks had been agreed, they were entered into a computer. Marks were
posted as quickly as possible on noticeboards in both hotels. Lists
were constantly updated, as were various pie-charts and histograms.
Once again, the efficiency was commendable.
Daily Diary
To try to give a flavour of how the IMO unfolded, I now offer a
brief summary of what happened day by day, as seen through my eyes.
17 July Leave home at midday to catch
flight to London, then on to Madrid. Meet Polish leader and Dutch
contingent. Settle down for long flight to Buenos Aires.
18 July Waken up to discover we have
touched down at San Paolo in Brazil. After another 2½ hours
reach Buenos Aires where temperature is a bracing -1° C. Transfer
to domestic airport by taxi. The 45-minute drive gives me a glimpse
of Buenos Aires. Meet up with lots of old friends for final flight to
Mar del Plata, which is 400 km south of Buenos Aires. The 737 is full
of IMO people. Should so many mathematicians all travel in the same
plane? Disembark at Mar del Plata on a glorious afternoon. Taken by
minibus to hotel. Door-to-door journey time of 30 hours. This hotel
is 5-star OK. It looks out over the Atlantic. Across the road is a
naval base which played a major part in a certain conflict in the
early 1980’s. Better not say too much about that! Have a very late
lunch. Pick up bag of goodies, 60 pesos and the short-listed
problems. Try a couple of problems but soon give up. Sleep for 12
hours.
19 July Renew many more friendships at
breakfast. Tables groaning with food. Does anyone really eat lemon
meringue pie at this time of day? Apparently so. First Jury meeting
is brief. After a few introductions, two matters are debated with the
chairman being overruled by the Jury both times. Off to a flying
start! Adjourn to try more problems. After lunch, stroll to the end
of the breakwater to get some fresh air. Solutions to the problems
now available. Try some more problems (without keeking at the
solutions!). At dinner we are serenaded by a harpist who plays a wide
selection of music, even parts of Verdi’s Rigoletto! After
dinner, there is a demonstration of how to do the tango. Some
preferred to get stuck into a book of crosswords supplied by the
Canadian leader.
20 July Selecting problems starts in
earnest. From the short list, 5 are chucked out because they have
appeared in some competition or other. More time still needed to try
problems ourselves. Adjourn until lunch. Write postcards. Walk
along the beach in bright sunshine. I really like this place! After
lunch there is a complex series of votes. What exactly is going on
here? By dinner we have chosen the 3 problems for the first day. Are
we proceeding in a sensible way? Philip, Michael and the team will be
on their way now.
21 July A long day! Morning spent trying
to finalise paper. Procedural wrangles aplenty. At 11.00 we seem to
be going OK, but by 12.00 things are distinctly pear-shaped. Feelings
running high. Mercifully, lunch intervenes. After lunch things get
more and more bizarre. Eventually we have our 6 problems. Not the
ones I’d have chosen individually (e.g. not enough geometry).
However, could be worse. Work starts on preparing master versions of
problems in English. Small group of English-speaking Leaders go off
to do the business. What will we call the matrices in Q4?
We must be able to improve on “coveralls”. Someone suggests
“silver” as a joke. Some Leaders think this is facetious but it
gets voted through! (A message arrives. The team have missed their
connecting flight from Buenos Aires to Mar del Plata because of late
arrival from London. Looks like a night in B.A. or a 5-hour train
journey starting at 23.30. I reply that Philip should decide on the
better option as he is the man on the ground.) English version
approved. Next come versions in French, German, Russian and Spanish.
Fun and games in Q1. We say “black and white”, the French say
“blanc et noir”, not “noir et blanc”! After several similar
arguments, next four versions are approved around 21.30. Time to
relax. Hope the team are OK. Just as well tomorrow is a free day.
22 July Hooray! The team have arrived OK.
Apparently they managed to get onto a later flight. First meeting not
until 11.30. A cosmopolitan group of Leaders (Canada, Colombia, New
Zealand, Switzerland, UK) have an invigorating 2-hour walk along the
beach. Cold to start with but soon the sun comes out. There are lots
of breakwaters. On every one, many local people are fishing. Back to
business, with approval given for over 40 more translations. After
lunch there is a joint meeting of the IMO Advisory Board and the Jury.
The IMOAB is responsible for planning ahead, finding future venues,
discussing rules and regulations, etc. There is a wrangle over
elections to the IMOAB. Then we have an open forum. At the behest of
BMOC I put the view that excessive training for IMO may harm the
mathematical development of students and I gain support from a number
of countries. Venues (some provisional) up to 2006 are announced.
Next year we go to Taiwan. At dinner we get the first edition of “La
Helice”, a daily IMO newsletter with contributions from students.
23 July Bus to Opening Ceremony. Leaders
are segregated in the gallery, with Deputy Leaders and Teams down
below. (We know the contents of the two papers and mustn’t
communicate with our students.) The lads are looking smart. Philip
throws up my team sweat-shirt, designed by Bennet. Things get going a
little late. After an introduction, we see a specially prepared film
of highlights of Argentina. The football goes down particularly well.
Then come speeches including one from the delightful Minister for
Culture and Education (representing President Carlos Menem). Next a
surprise. We have a new IMO song which receives its premiere. It is
to be sung at all future IMOs, apparently. This year’s version is in
Spanish, contains such wondrous lines as “Sumamos, multiplicamos y
llegamos a un total” and is entitled “Razonar es nuestro estilo”
(Reasoning is our style). This little ditty provoked a certain amount
of merriment but it isn’t quite as bad as it seemed at first.
Translations (including some irreverent ones by certain teams) are now
available in many languages. Proceedings end in a shower of balloons.
I give the lads the thumbs-up as they disappear. Off we go for a
barbecued lunch in the country. A bus trip of less than 5 minutes
(surely a record for IMO bus trips?) gets us to a Minizoo where a
water-pig takes exception to a peacock invading its enclosure. Back
to base for dinner and early bed.
24 July Up at 6.30. Off to Hotel 13 de
Julio for first paper. Turns out the teams are staying there, not 25
km away as expected. Jury gets installed before students go into exam
room. Students can ask questions during the first 30 minutes.
Questions have to be written down and are brought by runner to the
jury room. Queries are dealt with in order of receipt. The relevant
Leader has to explain to the Jury what the query says and how he/she
intends to reply. The reply has to be approved by the Jury before
being written down and taken back to the student by runner. Today we
get 56 queries, mainly about the meaning of max{m, n}.
Also “perpendicular bisector” seems to present problems in Spanish.
Off we go 70 kms into the pampas to visit the Juan Fangio Museum at
Balcarce. Fangio was world motor racing champion five times in the
1950’s. Examine cars he drove (Ferrari, Maserati, Mercedes-Benz) as
well as other old cars, including a Model T Ford. Next stop is a
barbecued lunch at an estancia (ranch). Entertainment consists of
traditional music and dancing. Another glorious afternoon. Back to
base, expecting to collect scripts from morning exam. Won’t be ready
until at least 21.30 because every page is being photocopied. By
23.00 there are still no scripts. Some Leaders are annoyed. I go to
bed.
25 July Another early kick-off. Today we
get 44 queries, mainly about the wording of Q4 and the meaning of
a(b2). After question time, back
to base to collect scripts. Quick glance suggests that some of the
lads have struggled on the first day. Bennet in good shape. Walk
down to meet the team as they come out of second paper (a brisk
50-minute stroll). Their view of Q1-Q3 agrees with mine. Philip and
Michael return from a trip to the aquarium and minizoo. Meet Carla,
the team guide, who seems to be getting on fine with the team. We all
have lunch together. First time we have been able to speak since
leaving the UK! Bennet’s hair is now red, white and blue, while Toby
has painted his finger-nails purple, presumably to express solidarity
with Bennet. Philip and Michael move to my hotel. After dinner, get
stuck into scripts for Q1-Q3. Around 21.30 Q4-Q6 arrive.
Co-ordination schedule appears. Reasonably early bed.
26 July Spend morning polishing up Q1-Q3
ready for the afternoon. Co-ordination very fair. Get one or two
more marks than expected. Philip and Michael in good form. Work on
Q4-Q6 before dinner. Scores going up on boards. Bennet’s three 7’s
are pleasing on the eye. After dinner, the crossword buffs are
reinforced by the Canadian and Irish Deputy Leaders. We have to
unravel something to do with The Spice Girls if we want to crack The
Listener Crossword, or so it seems.
27 July Spend morning polishing up Q4-Q6
ready for the afternoon. One or two unfortunate errors become
apparent and some of the lads lose marks that would have helped their
cause. Once again Michael and Philip produce order out of chaos.
After an adjournment to sort out Toby’s construction in Q4, we end up
with as many marks as we could reasonably expect. Meanwhile, I
supervise co-ordination of Argentina’s scripts for David Monk’s Q2, in
accordance with IMO rules for the host country. Results coming in
thick and fast but still too early to make confident predictions. At
dinner we all get a free cassette of “La Cancion de la Olimpiada”.
28 July Michael, Philip and I stroll down
to the students’ hotel to return scripts. The lads know how things
stand from scoreboards displaying the marks of all contestants. We
lunch together. Then it is the lads’ turn to experience the delights
of the minizoo. The three of us stroll back leisurely. We sample
alfajores, a local delicacy in the form of biscuits with toffee in the
middle and either chocolate or meringue on the outside. We also try
bocaditos, chocolate cones with toffee inside. They certainly like
their toffee in Argentina! The beach is heaving with people. It is
the mid-winter break when people come down to Mar del Plata from
Buenos Aires to stay in their chalets. Although it is mid-winter the
temperature is 21° C and the sun is shining. We see a variety of
entertainment, including several games akin to boule or
pétanque (a form of bowls). We return to base 7 hours after
leaving. A most enjoyable excursion giving us a chance to soak up the
atmosphere. Back at base, scores are virtually complete. We are
16th. After dinner it’s party time, courtesy of the Colombians. We
learn the salsa, which is a mere bagatelle for those who can do a
Dashing White Sergeant or Strip the Willow. As an interlude, Marta
Joltac, one of our superb organisers, entertains us with some Spanish
love-songs. Reinforcements arrive and the party goes on until 4 a.m.
I chicken out around 1 a.m.
29 July Open the curtains and can’t see a
thing for fog. Final Jury meeting attended by Deputy Leaders and
Observers. After a few arguments, marks are approved and cut-offs for
medals agreed. Vote of thanks to chairman, co-ordinators, etc. closes
proceedings. Go to a large sports centre to take part in all sorts of
physical activities. All in the line of duty, I help the lads to win
at tug-of-war and lose at 8-a-side football. (I have still a bruise
on my shin to show for my efforts.) A giant conga leads everyone back
to the buses. It’s the last night when we’ll all be together and we
spend it relaxing in various ways.
30 July Early breakfast then off to the
Closing Ceremony which starts at 09.00 (a time chosen, presumably, to
let teams fly out later in the day). Medals dished out. I manage to
catch the lads on camera. Bennet has reinforced his red, white and
blue hair-do specially for the occasion. Extra loud cheers for
medallists from Argentina. Then we see a video of highlights of the
IMO, prepared to a high standard during the night. The lads are seen
in pensive mood after one of the papers and Philip is spotted having
his lunch. Representatives from Taiwan extend their welcome for next
year and proceedings end with farewells from our hosts, accompanied by
much singing and waving of flags. Time for team photos, both formal
and in sweat-shirts. Back to the team hotel for lunch. The first
teams are starting to leave. Everyone gets a copy of the “Golden
Book” containing team pictures and statistics of the 38th IMO, again
produced very rapidly. The team go off to play frisbee with the
Americans. Philip, Michael and I stroll back to base. No sooner have
we got inside the hotel than a short sharp thunderstorm breaks, the
first real rain we have seen in Argentina. At dinner we get free wine
and another tango display. People start dancing again. We go to pack
but at midnight the party is still in full swing.
31 July The long trek home begins. Leave
hotel at 09.40 with fond farewells from our delightful hosts. Having
reached the main airport in Buenos Aires, we have 7 hours to kill.
Apart from eating, we play a curious game which is a mixture of blind
man’s buff and Cluedo, or so it seemed to me. Take-off is delayed by
100 minutes for “fuelling”. (Could they not have done it earlier?).
Eventually get going at 23.40.
1 August Dawn breaks over the Atlantic.
The lads are asleep. I’m not because I find it virtually impossible
on a plane. Breakfast arrives, time goes by and we land late at
Madrid. On the tarmac the temperature is 40° C. A bus takes us
to the sanctuary of the air-conditioned terminal. We’re off again
pretty sharpish and reach Heathrow at 18.15. Alas, no luggage. There
wasn’t enough time to transfer it at Madrid. Philip sorts things out,
we fill in forms, clear customs and emerge to be greeted by parents.
One more flight for me and I get home at 22.20. Journey time
(allowing for 4 hours difference in local times) 32 hours 40 mins.
The odyssey is almost complete, but not quite.
2 August At 19.40 my missing luggage is
delivered. Now I can start writing this report!
Concluding Remarks
IMO97 will go down as one of the best IMOs ever, thanks to our
Argentinian hosts. As soon as we arrived, we received a warm welcome
which lasted right through to departure. As previously remarked, the
organisation was superb, with some nice little touches which
epitomised the meticulous attention to detail. The whole atmosphere
was delightful, with old friendships renewed and many new friendships
made. To everyone involved in making our stay so enjoyable we extend
our heartfelt thanks.
Nearer home, I should like to thank
- all the pupils who took part at any stage
- all the teachers who encouraged the pupils and supported our
endeavours
- Peter Neumann for his skilful chairmanship of BMOC (and now
UKMT)
- the Problems Group for creating so many interesting problems
- Alan West and Brian Wilson, organisers of BMO 1 and BMO 2
respectively
- all those involved with the marking of BMO 1, especially Brian
Wilson and Christine Farmer
- all those who contributed to the Trinity Training Session
- all our sponsors, especially Trinity College, Cambridge for
hosting the April training session and the Royal Society for
hosting the September celebration
- DfEE for a grant covering travel to and from Argentina
- Tim Cross for producing the 1997 BMO booklet, 175 copies of
which were taken as gifts for Leaders, Deputy Leaders and our
Argentinian hosts
- Philip Coggins for assistance with the correspondence course
and, along with Michael Davies, for help of all sorts before and
during the visit to Argentina.
That leaves us with the 7 members of the squad. The majority have
been in the system for several years but are now leaving us to start
the next stage of their mathematical education at university. Their
enthusiasm over the years has been remarkable and it has been a
privilege and a pleasure to work closely with them. They have been
excellent ambassadors. Let us salute them for their achievements this
year and in previous years and let us wish them all the best for the
future.
Return to IMO Register home page
Contact: Joseph Myers
(imo-register@imo-register.org.uk)
Online HTML version last updated:
5 January 2016
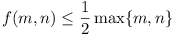 for all m and
n.
for all m and
n.![]()
![]()