39th INTERNATIONAL MATHEMATICAL OLYMPIAD
TAIPEI, TAIWAN
10-21 July 1998
Report by ADAM McBRIDE (UK Team Leader)
Introduction
The best laid schemes o’ mice an’ men gang aft
a-gley.
So wrote Robert Burns in his poem To a Mouse. The quotation
provides an apt description of the climax to the UK team’s
preparations for this year’s International Mathematical Olympiad
(IMO). Everything had gone smoothly during the selection and training
of the team. However when it came to the flight from Heathrow to
Taipei, things went badly wrong. Because of air traffic control
problems, the team missed their connection at Amsterdam. They had to
stay in Amsterdam for almost 24 hours before embarking on a 16-hour
flight to Taipei via Bangkok. They arrived at their accommodation a
mere 15 hours before the first paper (and missed the Opening Ceremony
as a result). Their luggage was delayed even longer, so that team and
luggage were only reunited a mere 2 hours before the first paper.
Needless to say, everyone was exhausted both physically and mentally,
hardly an ideal condition in which to tackle two 4½-hour
papers. Under the circumstances, the team performed remarkably well
and I congratulate all the students on their achievements.
Apart from the difficulties described above, this year’s IMO was an
enjoyable experience. Almost without exception, the organisation was
good. Accommodation for the Leaders was luxurious, almost
embarrassingly so at times. The accommodation for the students was
rather more basic, especially the beds each of which was essentially a
plank of wood and a sheet. However, there were no complaints about
the food and other facilities were more than adequate. Our hosts were
always gracious and cheerful, going out of their way to make us feel
welcome. The weather was dry but humid, with record temperatures of
over 100°F being recorded. Fortunately, air conditioning was on
hand most of the time. After the papers had been sat, there were
various excursions and social events. By this time everyone had
almost recovered from jet-lag so that the IMO ended on a happy note.
All of us will have fond memories of our visit to Taiwan.
Selecting the UK IMO team
As usual things got under way on the third Friday in November with
the UK Senior Mathematical Challenge (UKSMC), a 1½-hour paper
containing 25 multiple-choice questions, of which the first 15 are
intended to be accessible to most contestants and the rest are meant
to be more taxing. The 1997 UKSMC attracted a record entry of over
44000 students. It is hoped that the number of contestants will
continue to increase in future years. Of course, more entrants
produce more work for the organisers. However, the results were
processed very smoothly and efficiently thanks to the efforts of Bill
Richardson (Chairman of the Senior Challenges Subtrust of the United
Kingdom Mathematics Trust) and Heather Macklin (Maths Challenges
Office, University of Leeds).
Around 800 pupils went forward to the British Mathematical
Olympiad, Round 1 (BMO1), a 3½-hour paper with 5 questions held
in mid-January. Of these around 100 were invited to take part in
Round 2 (BMO2), another 3½-hour paper with just 4 questions,
held at the end of February. On the basis of the marks scored, it
would seem that BMO2 was found easier than BMO1.
At this stage, it is appropriate to repeat a comment made in my
reports for 1996 and 1997. Of the 100 or so contestants in BMO2, only
9 were girls. Of the 67 schools represented, 60 are in England, 4 in
Scotland, 2 in Northern Ireland and 1 in Wales. The small number of
girls and the small number of schools outside England are sources of
concern. We should all redouble our efforts to rectify the situation.
Based on all the information available, exactly 20 students were
selected for a residential Training Session at Trinity College,
Cambridge in early April. In addition to all the serious contenders
for this year’s IMO team, some younger students were blooded as an
investment for the future. Each day there were 4 or 5 intensive
sessions on Algebra, Combinatorics, Functional Equations, Geometry,
Inequalities and Number Theory. In each session the emphasis was on
tackling problems, with the bare minimum of exposition from the person
leading the session. Thanks are due to all who gave so willingly of
their time to prepare material and lead sessions. Special thanks to
Julia Gog for the domestic arrangements which helped to make the
Training Session so enjoyable and successful.
The climax of the Trinity Training Session was the Final Selection
Test (FST), a 4½-hour paper with just 3 questions, mirroring
the structure of an IMO paper. In the event FST was possibly too
hard, with most students scoring very few marks. On the basis of
BMO1, BMO2 and FST performances, an IMO squad of 8 students was chosen
and they immediately embarked on a correspondence course. They
received a sheet of 8 or 9 problems every 10 days and had to submit
solutions in accordance with strict deadlines. Towards the end of
May, our selection was finalised as follows:
| Team: | Mansur Boase (St. Paul’s School, London) |
| Mohan Ganesalingam (Westminster School, London) |
| Luke Halliwell (Madras College, St. Andrews) |
| Toby Kenney (Calday Grange Grammar School, Wirral) |
| Robert Morris (Lancaster Royal Grammar School) |
| Jeremy Young (Nottingham High School) |
| Reserves: | Rebecca Palmer (Clitheroe Royal Grammar School, Lancashire) |
| Peter Youngs (St. Paul’s School, London) |
| Team Leader: | Adam McBride (University of Strathclyde, Glasgow) |
| Deputy Leader: | Philip Coggins (Bedford School) |
| Observer: | Richard Atkins (Oundle School, nr. Peterborough) |
Sending an Observer to the IMO allows interested parties to see at
first hand what is involved in being either the Leader or the Deputy
Leader. On this occasion Richard shadowed Philip.
Final Preparations
The correspondence course continued until the beginning of July,
with occasional interruptions because of A-levels and other exams.
During the period 1-5 July, the team gathered at Queen’s College,
Birmingham in conjunction with the National Summer School being run
there by Tony Gardiner. There were further sessions on Combinatorics,
Geometry and Number Theory, as well as 2-hour mini-papers and another
mock IMO paper. An important objective was to get to know each other
better and to develop team spirit. One session was devoted to a “pep
talk” while Philip dealt with travel arrangements, medical precautions
and all the other small things that can be useful in an emergency.
Team T-shirts, designed by Luke, were dished out. For light relief we
saw a hilarious open-air performance of Much Ado About Nothing
in which Shakespeare’s text underwent some interesting
transformations. There was also a “Mathematical Mélange” in
which the younger students at the Summer School displayed their
abilities in a wide range of music, plus a bit of juggling. The
Summer School was a great success and a fitting conclusion to our
preparations. We are all most grateful to Tony Gardiner for the huge
amount of work he put into its organisation.
Timetable of the 39th IMO
The Jury, comprising the Team Leaders of all competing countries,
met for the first time on the evening of 10 July and spent the next
three days selecting the problems for the two papers and approving the
translation of the papers into all the required languages (48 in
total). The Teams arrived (or were supposed to arrive!) on 13 July
and the Opening Ceremony was on 14 July. The two examination papers
took place between 09.00 and 13.30 on 15 and 16 July. Thereafter the
contestants could relax and go on excursions while the Leaders and
Deputy Leaders embarked on two days of marking and co-ordination. The
Closing Ceremony, including the presentation of medals, took place on
20 July and proceedings concluded with a Banquet.
The Problems
All contestants sat two papers on consecutive days. Each paper
contained three problems, each problem being worth 7 points.
On each day the time allowed was 4½ hours.
The problems were proposed by the countries indicated.
FIRST DAY
-
In the convex quadrilateral ABCD, the diagonals
AC and BD are perpendicular and the opposite sides
AB and DC are not parallel.
Suppose that the point P, where the perpendicular
bisectors of AB and DC meet, is inside ABCD.
Prove that ABCD is a cyclic quadrilateral if and only if
the triangles ABP and CDP have equal areas.
(Luxembourg)
-
In a competition, there are a contestants and b
judges, where 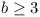 is an odd integer. Each judge
rates each contestant as either “pass” or “fail”.
is an odd integer. Each judge
rates each contestant as either “pass” or “fail”.
Suppose k is a number such that, for any two judges,
their ratings coincide for at most k contestants.
Prove that
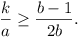
(India)
-
For any positive integer n, let d(n)
denote the number of positive divisors of n (including 1
and n itself).
Determine all positive integers k such that
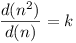
for some n.
(Belarus)
SECOND DAY
-
Determine all pairs (a, b) of positive integers
such that
ab2 + b + 7
divides a2b + a + b.
(United Kingdom)
-
Let I be the incentre of triangle ABC.
Let the incircle of ABC touch the sides BC,
CA and AB at K, L and M,
respectively.
The line through B parallel to MK meets the lines
LM and LK at R and S, respectively.
Prove that 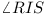 is acute.
is acute.
(Ukraine)
-
Consider all functions f from the set N of all
positive integers into itself satisfying
f(t2f(s)) =
s(f(t))2
for all s and t in N.
Determine the least possible value of f(1998).
(Bulgaria)
You are invited to send in solutions, enclosing an
SAE please, to
Adam McBride, Department of Mathematics,
University of Strathclyde, Livingstone Tower,
26 Richmond Street, GLASGOW G1 1XH.
Comments on the Problems
Participating countries submitted 122 problems, with geometry once
again the most popular area. The organisers produced a short list of
28 problems for consideration by the Jury. The United Kingdom
submitted 6 problems, of which 3 were composed by David Monk (formerly
University of Edinburgh), 2 by Christopher Bradley (Clifton College,
Bristol) and 1 by Kevin Buzzard (then at Trinity College, Cambridge).
All three of David’s problems were included in the short list and one
was used as the first problem on the second day. This remarkable
achievement reflects David’s knack of producing a seemingly endless
stream of interesting problems. Thanks to David, Christopher, Kevin
and others, we are well blessed with first-rate problemists.
How the UK Team Performed
A total of 419 contestants from 76 countries took part (slightly
down on 1997). The UK team finished 17th (equal) out of 76 with 122
points (out of 252). Team members won
1 Silver Medal, 4 Bronze Medals and 1 Honourable Mention.
Individual scores were as follows:
| Mansur Boase | 13 | Honourable Mention |
| Mohan Ganesalingam | 30 | Silver Medal |
| Luke Halliwell | 15 | Bronze Medal |
| Toby Kenney | 22 | Bronze Medal |
| Robert Morris | 20 | Bronze Medal |
| Jeremy Young | 22 | Bronze Medal. |
These bald statistics must not be taken at face value in view of
the difficulties mentioned at the start. Mansur and Luke were
particularly badly affected by all the hassle and the lack of sleep.
Mansur missed out on a medal by just one point but had the consolation
of gaining an Honourable Mention for scoring full marks on one
particular problem.
Overall Performance of All Contestants
In general, scores were slightly lower than last year. The ranges
of scores for the various medals were:
| Gold | From 31 to 42 | (37 contestants) |
| Silver | From 24 to 30 | (66 contestants) |
| Bronze | From 14 to 23 | (102 contestants). |
Only one contestant (from Iran) scored full marks.
Of the six problems, the last one produced far and away the lowest
scores. Indeed, 340 students scored 0 on this question. This came
about partly because of the difficulty of the problem and partly
because of the rather draconian marking scheme.
Although the IMO is, strictly speaking, an individual competition
and, officially, there is no team competition, considerable interest
still attaches to team totals. For the record, here are the top 20
teams with their totals out of 252:
| 211 | Iran | 195 | Bulgaria | 186 | Hungary, USA |
| 184 | Taiwan | 175 | Russia | 174 | India |
| 166 | Ukraine | 158 | Vietnam | 156 | Yugoslavia |
| 155 | Romania | 154 | South Korea | 146 | Australia |
| 139 | Japan | 135 | Czech Republic | 129 | Germany |
| 122 | UK, Turkey | 118 | Belarus | 113 | Canada. |
Organisation of the 39th IMO
The logistics of running an IMO are very complicated. Getting a
crowd of mathematicians from A to B is notoriously difficult.
Fortunately, we had a group of delightful young ladies to keep us on
the right track. They made sure that nobody got left behind and also
cheerfully helped to answer queries and sort out any problems that
arose.
Each of the teams is allocated a guide, normally a postgraduate or
senior undergraduate who can speak the appropriate language. The UK
team’s guide, Sophie, was studying English so that there were no
communication problems! Sophie’s jobs included making sure that
everyone turned up in time for the exams and that nobody got lost on
the excursions. She also rose nobly to the challenge by getting
emergency supplies of shorts, T-shirts and sandals to tide the team
over until their luggage arrived. The team showed their gratitude by
presenting Sophie with a large cuddly toy in the form of a bear.
All decisions concerning the actual competition were in the hands
of the Jury which comprised the 76 Team Leaders, each of whom had one
vote. We each had a plastic wand with our own 3-letter code marked on
it. The UK code was UNK so that, as usual, I was “The Man from UNK”
(as opposed to “The Hunks from UNK”, who were elsewhere in town!).
Votes came thick and fast and majorities were based on the number of
wands raised. The business of the Jury was conducted in English, with
occasional translations into other languages when required. A good
chairman is needed to avoid the whole thing turning into a bear
garden. Fortunately, we had the services of Professor Jen-chung Chuan
who presided with a judicious mixture of firm control and good humour.
For security reasons, the Jury were in a luxury hotel cum beach resort
25 kilometres out of town until the end of the second paper. Then
Leaders moved to join Deputy Leaders in another 5-star hotel, this
time in the middle of Taipei.
With Leaders and Deputy Leaders all together, marking of scripts
and co-ordination got under way in earnest. We had to mark our own
team’s scripts and then justify our marks before a panel of
co-ordinators. It was up to Philip Coggins, Richard Atkins and myself
to get as many marks as possible for our students on the basis of the
scripts which had been presented to us. The three of us worked
splendidly as a team and I should like to thank Philip and Richard for
their sterling contributions. After the exam, the organisers had
photocopied every sheet of paper submitted by every student. Co-ordinators
were thus able to read scripts in advance and get a feel
for various methods of solution used by students. As a result,
co-ordination was speeded up considerably. Discussions, while
sometimes intense, were always amicable and any disputes were
satisfactorily resolved (in one case after a break for lunch!). As
soon as the marks for a question had been agreed, they were posted on
noticeboards in our hotel and in the students’ accommodation so that
everyone was kept up to date with developments. For the most part,
things were done with commendable efficiency.
Daily Diary
To try to give a flavour of how the IMO unfolded, I now offer a
brief summary of what happened day by day, as seen through my eyes.
9 July Another IMO odyssey gets under way. What lies ahead,
I wonder? Leave home at midday to catch a flight to Amsterdam. Meet
half a dozen other Leaders. The teams from The Netherlands and Russia
are also there. At their own expense they are going 3 days early to
get acclimatised (something we might think about for the future, given
this year’s experience).
10 July How do you get a decent sleep on a jumbo jet? I
hardly sleep a wink. Entertainment is provided by The Full
Monty, The Man in the Iron Mask and a hilarious Rowan
Atkinson short. On a radio channel, the Brahms Violin Concerto comes
round every hour or so. After 11½ hours we touch down at
Bangkok. There seems to be a golf course right beside the runway with
no boundary between. Do golfers give way to aircraft or vice versa?
After a short break, another 3½ hours in the air get us to
Taipei. The temperature is 27°C, a bit on the cool side because
of a possible typhoon, we are told! During the 1½-hour drive
to the hotel, I get my first impressions of Taipei. The streets are
full of motor scooters and yellow taxis. Memories of Bombay two years
ago but here the city is cleaner, the driving is better and people
don’t blow their horns so much! Check-in at the hotel is mildly
chaotic. I find myself sharing a room with Gregory, the Leader from
Cyprus, an amiable chap. It’s taken almost 24 hours door-to-door but
there’s no rest yet. No time for dinner either as the first Jury
meeting gets under way. The meeting is relatively short. After a
quick look at the short list of problems, I crash out.
11 July Woken at 5 a.m. by wind and rain. The south of the
island has caught the typhoon, but we escape lightly. I’ve seen worse
in Glasgow on many a day! This turns out to be all the rain we see
during the entire visit. We set sail on pruning the short list.
Problems are classified as of either Primary or Secondary interest. A
problem was defined as being of Secondary interest if it had already
been published or if someone didn’t like it. We make good progress
thanks to our efficient chairman. After lunch, Primary problems are
sorted into Easy, Medium and Hard. At one stage there is a procedural
wrangle over the difference between a “suggestion” and a “motion”.
You can second a motion but can you second a suggestion? The barrack
room lawyers were in fine form. Eventually after a long day we
adjourn to prevent people talking any more nonsense. There is
open-air dancing for those with sufficient energy. I settle for
writing a few postcards.
12 July Good progress during the morning. We choose 5
problems out of 6 and adjourn to decide on a second geometry problem,
of which there are still 7 available. We vote by elimination, the
least favourite problem dropping out each time. Alas, my favourite
problem bites the dust. We are left with a choice of one from two.
The vote is a tie! The chairman does not use his casting vote but
calls a brief adjournment, after which we vote again and this settles
the paper (or so we thought). The Australian leader and I supervise
the preparation of the English version of the papers, paying due
regard to wording, notation and the spelling of “incentre”. Just when
everything seems tickety-boo, a mathematical typhoon hits us. It is
discovered (rather belatedly and by sheer serendipity) that one of our
chosen problems is very similar to one discussed in a recent book
review in Crux Mathematicorum, which some students will have
seen. Panic stations! I call for an adjournment to allow us to take
stock. We resume at 22.00 and decide that the chosen problem must be
replaced. The late hour leads to more people talking nonsense. Did
we vote on something or didn’t we? Nobody is sure. Definitely time
for bed.
13 July After further brief debate, the revised papers are
agreed. Not the best outcome in my opinion and rather too much Number
Theory, but we are stuck with it. French, German, Russian, Spanish
and Chinese versions are prepared and approved. Leaders now use one
of the six “authorised versions” as a basis for their own
translations. In all, versions in 48 different languages are needed.
I relax by going down to the beach. When I return, I get the first
hint of trouble ahead. There is a list of all the teams which have
arrived safely. No sign of the UK! In response to urgent enquiries,
I eventually get a copy of a FAX from Philip, saying “all well, but
stuck in Amsterdam!”. New arrival time is 13.00 tomorrow. Bad news!
The team will arrive very tired and will miss the Opening Ceremony.
Retire to bed, grumpy.
14 July Up at 05.30, breakfast at 06.00, then off by bus to
the Opening Ceremony at Taipei International Conference Centre. The
journey of 25 km takes 1½ hours in the heavy traffic. We have
to be segregated from the students because we know the problems in the
exam. As a result we hang around for 2 hours. When things get going,
there is a distinct lack of atmosphere. The hall is far too big and
most of the speeches are boring. A school orchestra entertain us with
music by Bizet and Johann Strauss. The Prime Minister is due to make
a speech but is delayed because he is busy sacking his Minister of
Justice. So the orchestra play most of their repertoire again to fill
in time. The fact that my team were still in a plane didn’t help
matters (although they didn’t miss much on this occasion). After a
quick kip, I head for the beach but find nobody there. Something to
do with mad dogs and Englishmen, I suspect! After 5 minutes in the
baking heat, I retreat. At 16.00 there is a joint meeting of the Jury
and the IMO Advisory Board, the body which keeps things ticking over
between IMOs and plans for the future. There are two contentious
issues: the role of Observers at co-ordination and the status of
students from one country who are temporarily studying in another
country. Much heat is generated but eventually common sense prevails.
Following elections to the IMOAB, the meeting is adjourned
(unfinished) after 3 hours. We then have a round table dinner of
Chinese food. There are ten courses, with lots of seafood. Strange
parts of strange creatures are consumed with no obvious ill effects!
Get confirmation of team’s arrival.
15 July Another early start as we head for the National
Taiwan Normal University for the first paper. Contestants may ask
questions during the first 30 minutes. These questions are written
down on special paper and brought by messenger to the Jury which
decides, by vote if necessary, on a suitable response. Someone had
the bright idea of introducing modern technology. As a result the
meeting is a shambles. Too many people run around getting in the way
and the computer is more of a hindrance than a help. It takes 75
minutes to handle 23 questions (mostly about the meaning of the term
“cyclic quadrilateral”), which is not satisfactory. A simpler, more
efficient system is requested for the second day. Outside it is
hotter than ever. I wonder how the lads are getting on. I’m sure
Philip and Richard will do their best to keep spirits up. Tomorrow we
switch hotels and I do some preliminary packing. The present hotel
throws a farewell cocktail party. At the end the scripts for the
first paper arrive. I decide to go to bed without looking at them,
otherwise I won’t get any sleep at all!
16 July Up again at 05.30, luggage in the lobby at 06.20,
off to NTNU at 07.00 for the second paper. We get 28 queries (mainly
asking if 0 is a positive integer) but we polish them off much more
quickly than the previous day. There have been complaints about the
draft marking scheme and the Chief Co-ordinator is summoned. While we
await him, the IMOAB business held over from 14 July is completed.
There is a long discussion on the mark scheme and a planned visit to
the Chiang Kai-Shek Memorial Hall is cancelled. We transfer to our
new hotel, every bit as luxurious as the previous one. The view out
of the window is interesting. When the traffic lights change, several
hundred scooters swarm forward like ants. I meet up with Philip and
Richard, who tell me the full story about the delays and missing
luggage. The situation was worse than I realised. Back to NTNU to
meet the lads as they come out of the exam. Although exhausted, they
are in remarkably good heart. We have lunch and they tell me how they
think they have done. Their predictions turn out to be pretty
accurate. Back to base to start marking with Philip and Richard.
17 July During the day we co-ordinate problems 2, 3 and 5.
At lunch the Irish leader asks if we felt the earthquake. What
earthquake? It turned out that there had indeed been an earthquake
registering 6.2 on the Richter Scale. The epicentre was about 100 km
south of Taipei and 5 people had been killed. Considerable structural
damage occurred. In our hotel, people on the upper floors reported
that doors and windows shook for about 40 seconds. The Brits were
unshaken! After lunch, we prepare questions 1, 4 and 6 for the next
day. Looks as though most people will get zero on Q6 because of the
mark scheme. Philip and Richard head off for Snake Alley, the venue
for a night market where you can buy all sorts of interesting things!
I pass on that one.
18 July A busy morning. In addition to co-ordinating
questions 1, 4 and 6 for our team, Philip and I have to act as
co-ordinators for the attempts at David Monk’s Q4 by the Taiwan team.
After an adjournment over lunch to resolve one dispute, we are
finished. It is Saturday (I think, but you tend to lose track!) and
Philip, Richard and I go for a stroll round two weekend markets, one
for flowers and one for jade. These are held under a motorway in what
is a car park during the week. Doesn’t sound too attractive but at
least you are out of the sun! Back at the hotel, most of the scores
are now posted. We are heading for 17th equal. It looks as though
the cut-offs for the medals won’t do us any favours. A game of bridge
gets going. At one stage there is an interruption when the Russian
Observer seeks help in the matter of projective geometry. Apparently
the co-ordinators do not understand what seem to be perfect solutions
to Q5 by a number of students. We support our Russian colleague but
the dispute goes on well into the night.
19 July At last an excursion, to the National Palace Museum,
the home for Chinese treasures of great antiquity. We inspect lots of
porcelain, jade, carvings and ancient books. Outside the temperature
is over 100°F. Back to NTNU for the final Jury meeting to confirm
results. Go to see the lads and examine their living quarters. The
beds sure are basic! We all have dinner together. A disco party gets
going for the students. The rest of us are supposed to be going to
another party which promised an evening of “fun and good times”. This
turned out to be very noisy music in a pub. Richard displayed
commendable fortitude, but Philip and I settled for a walk back to the
hotel, quite pleasant in the (relative) cool of the evening (only
90°F now!).
20 July Spend a quiet morning packing. After lunch we have
the Closing Ceremony, a three-hour affair containing speeches,
entertainment and medal presentations. The highlight of the
entertainment was a chair building routine by an acrobatic troupe. We
started with a small chest mounted on four legs. Four empty wine
bottles were put on top of the chest. Then a chair was balanced on
top of the bottles, one leg on each bottle. A young lad was perched
on the chair. One by one, more chairs were handed up to him and the
tower got higher and higher. By the end the lad was near the roof on
top of about 10 chairs. (Coming down wasn’t trivial either!) Back at
ground level, students went up for their medals in groups of 6 or 7.
I managed to get a picture of the big moment for each of our lads.
Outside it was time for team photos. The students came back to our
hotel for the Closing Banquet, a bit of a cultural shock for them. It
was another 10-course round table business. Entertainment was
provided by a percussion group, a singer who sounded as if she was
being strangled and a moderately good magician. Some teams were
leaving in the early hours and so it was time for farewells all round.
Many new friendships had been made and lots of addresses were
exchanged. The evening brought the official proceedings to a happy
end.
21 July One of those days you can do quite well without when
all you want to do is get home. Spend a lot of time sitting in buses
which are going nowhere. Luggage gets shuffled around from one place
to another. Our flight is not until 19.40 so that there is a lot of
time to kill. Many other teams are on the same flight which raises
the question as to whether so many mathematicians should all travel
together (coplanar mathematicians in the language of one of Philip’s
better jokes!).
22 July Arrive at Heathrow around 07.40 after a trouble-free
journey. (Would that this had been true on the outward trip.) Chat
to some of the parents before we all head our separate ways. One more
flight to Edinburgh. Home by 12.30. It is raining and the
temperature is 60°F. Normal service has been resumed.
Concluding Remarks
IMO 98 will prove to be a memorable experience for all of us. Some
things we could have done without. Nevertheless, we have brought back
many happy memories of Taiwan and the warm hospitality of our hosts.
The whole process, which started away back in November, involved
lots of people. In particular, I should like to thank
- all the pupils who took part at any stage
- all the teachers who encouraged the pupils and supported our
endeavours
- Jim Wiegold and Peter Neumann, the chairmen of BMOC and UKMT,
for their interest and encouragement
- the Problems Group, notably David Monk, Christopher Bradley and
Kevin Buzzard, for creating so many interesting problems
- Bill Richardson and Heather Macklin, organisers of the UKSMC
- Alan West and Brian Wilson, organisers of BMO1 and BMO2
respectively
- all those involved with the marking of BMO1, especially Brian
Wilson and Christine Farmer
- all those involved with the Trinity Training Session, especially
Julia Gog
- all our sponsors, especially Trinity College, Cambridge for
hosting the April training session and the Royal Society for
hosting the September celebration
- Tony Gardiner for organising the Summer School and for much more
besides
- DfEE for a grant covering travel to and from Taiwan
- Ben Meisner for producing the 1998 BMO booklet, 200 copies of
which were taken as gifts for Leaders, Deputy Leaders and our
Taiwanese hosts
- Richard Atkins for being an excellent Observer and, notably,
retrieving the luggage from the airport
- Philip Coggins for assistance with the correspondence course and
for help of all sorts before and during the visit to Taiwan.
That leaves us with the 8 members of the squad. Their attitude
throughout was excellent and the quality of work produced, often under
pressure, was consistently high. Our two reserves, Rebecca Palmer and
Peter Youngs, made the others fight hard for a place and thereby made
a valuable contribution to the team effort. The majority of the squad
are now leaving us to start the next stage of their mathematical
education at university. They have been excellent ambassadors and it
has been a privilege and a pleasure to work closely with them. Let us
congratulate them on their achievements and wish them all the best for
the future.
Return to IMO Register home page
Contact: Joseph Myers
(imo-register@imo-register.org.uk)
Online HTML version last updated:
5 January 2016
![]() is an odd integer. Each judge
rates each contestant as either “pass” or “fail”.
is an odd integer. Each judge
rates each contestant as either “pass” or “fail”.![]()
![]()