UK IMO team leader’s report
Dr Geoff Smith, University of Bath
After IMO 2001 in Washington, I took over as UK leader from my
eponymous predecessor Imre of that ilk. I had been recruited over
lunch at Trinity College Cambridge by Adam McBride. His references to
“willingness to serve” initially led me to believe that he was either
about to offer me a job on the college staff, or to suggest a game of
tennis. Naturally my first thoughts concerned who had already turned
the job down, but Adam gallantly assured me that no-one had done
so. It seemed unlikely that this was an outright lie, but it all
seemed very odd. Then the truth struck me. Everyone with the
appropriate experience and talent was tied up running the forthcoming
IMO in Glasgow, so Adam was being forced not so much to scrape the
barrel as to gouge it.
It so happened that I had already planned a trip to Budapest in the
aftermath of the Washington IMO. This took on a new significance, and
thanks to the kind help of Richard Rimanyi, a Hungarian singularity
theorist I had met through a conversation in a Turkish bath, I was
introduced to the Hungarian IMO establishment. Happily I already knew
their leader Jozsef Pelikan because of our mutual interest in group
theory. Sandor Dobos is the Hungarian deputy leader and chief trainer,
and he proved very helpful. Sandor and I started to develop plans for
joint training under the auspices of the Bolyai Society.
Upon returning to the UK, these plans were refined with the help of
our splendid deputy leader Richard Atkins. We received generous
backing from the BMOS and UKMT for a much expanded training
programme. Richard and other sages, gurus, veterans and relics of the
British Mathematical Olympiad scene helped me to draw up a list of
likely prospects for the UK IMO team in 2002. These students gathered
for our first training camp at the University of Bath in September
2001. We did a great deal of mathematics, and the students started the
process of bonding into a squad. We had sessions from many experienced
trainers, and UKMT supremo Peter Neumann also paid a visit. The
attacks on the United States on September 11th happened
during this camp, and the mood quietened as we reflected on the New
Yorker who had been the UK’s guide in Washington, and everyone else
caught up in the trauma. Happily the guide and his family were safe,
but one of the senior executives of the Akamai foundation (one of the
main sponsors of IMO Washington) had been killed.
During the Autumn of 2001 the advanced mentoring scheme kicked in
for the new squad of 15 students, and we decided to have monthly
exams. At this stage Tim Austin, Nathan Bowler and Paul Jefferys were
the leading candidates for places in the team, but the remaining three
places were wide open.
After Christmas we gathered at Heathrow and travelled to
Budapest. Our Hungarian friends had organized a wonderful mathematical
programme. We stayed in a boarding school in conditions which were
perfectly comfortable but came as something of a surprise to the less
well-travelled students. In particular, the collective shower rooms
were a novelty. Of course, Richard and I had grown up in an era when
the treatment of teenagers was more robust than today. The girls took
action and posted a rota and warning sign on the door of their shower
room. The male reaction was muted, and the more sensitive souls took
to showering in the middle of the night (if at all).
A research student from the University of Bath, Ceri Fiddes, was
there to provide adult support to the four girls who came on the
trip. Every morning we had lectures from Hungarian academics, and in
the afternoons we worked on problems with the Hungarian squad. In the
late afternoon the students presented their solutions, and in the
evening the UK squad sought to undermine the future of Hungarian
mathematics by teaching a pointless but addictive card game called
Mao. New Year celebrations in Budapest were a great success. Tim
Austin’s birthday was celebrated by the presentation of a remarkable
polychromatic jester’s hat, replete with fronds, bells and so on.
Jozsef Pelikan gave a tour de force lecture on algebraic number
theory from the ground up. His lecture (without notes) started at
9:00 am and finished at 1pm. He kindly agreed to our request for a tea
break of 10 minutes in the middle. It was an exhilarating experience,
and many of the students were on the edge of their seats.
We moved residence to a hotel in a suburb of Budapest called
God. Over the road was another suburb called Alsogod. Thankfully
inspiration (divine or otherwise) was at hand when our students sat
the third round of the Hungarian Mathematical Olympiad, and they did
quite well. The exam room was an airy wood panelled room with a
glorious view over a garden to the Danube. In the evening there were
snowball fights, and the impudent Paul Jefferys had the cheek to throw
one at me. The Hungarian trip was a delight, and we must thank the
Hungarian students and their brilliant trainer, Sandor Dobos.
As we returned to the UK, I went on sabbatical to the Institut
Henri Poincare in Paris, but returned to London for a week-end to help
with marking the first round of the British Mathematical Olympiad. We
expected that the students in the UK squad would perform very well in
BMO1 because of their extra training, and indeed this
happened. Richard and I were watching carefully for evidence that we
had missed some strong students, and after BMO2 (marked in Paris) we
added some new names to the UK IMO squad for the Trinity Camp at
Easter. The traditional FST (final selection test) was renamed the
first selection test. As a result of the FST, both Martin Orr and Tim
Northover were added to the squad, and some other students were
rested.
After Trinity the training regime became more intensive, with a
problem sheet once every 10 days. At the start of June we had a camp
at Oundle School over the Golden Jubilee week-end. At this stage we
were joined by a film company who had been commissioned by BBC2 to
make a documentary including our preparations for (and participation
in) the Glasgow IMO. The director is Stephen White, and we understand
that the programme will be shown in 2003. This provided an unusual
backdrop to the preparations for the IMO. After Oundle we made the
final selection of the team shown in the marks table below. Bryn
Garrod, Tim Northover and Martin Orr were standing by as very capable
reserves.
The final run-up to IMO 2002 consisted of a week in Birmingham in
parallel with the National Mathematics Summer School, and then a week
at Trinity College Cambridge. By now the team were taking a mock IMO
examination every day. The journey between Birmingham and Cambridge on
the UK IMO bus was enlivened by Stephen’s film crew buzzing around on
the motorway, taking footage for the documentary.
In Cambridge we continued the preparation. Diversions included a
punting trip and a visit to the Wren library to view Hardy-Ramanujan
correspondence, the original Winnie-the-Pooh manuscript and other
similar items.
The IMO
The leaders’ hotel was in Dunblane, temporarily renamed
Brigadoon. A house near the hotel carried a small plaque on which it
was explained that Charles Edward Stewart has spent the night at that
residence on September 11th 1745. The failure of the
Jacobites to secure the Catholic succession was reflected in the
conduct of the 43rd IMO. The first jury meeting was chaired
by John Knox, who had risen from the dead and donned an Adam McBride
mask for this purpose. He peered into our souls, and was not
impressed.
The leaders were told about their duties and responsibilities in
considerable detail. Telephone communication with the outside world
was cut off and the Black Watch had the hotel surrounded. The preacher
grudgingly conceded that (regretfully) we were in a democracy, and
leaders could swan off if they wished, but then he reminded us of our
consciences, and the indelible stain that we would carry if we
neglected our obligations in any way. The McBride impersonator spoke
more and more slowly to make sure that any non-Presbyterians present
would get the point. Between invocations of wrath and damnation, at
first between sentences, and later between words, time seemed to
stop. He used these gaps to demonstrate exquisite control over his
features, eyeballs throbbing in their sockets until inevitably they
began to revolve in opposite directions.
Peter Neumann was allowed to make a few welcoming remarks by way of
intermission, before the chairman reasserted his authority and
continued to enumerate a rather interesting list of human weaknesses
to which we should not fall prey, including sloth, tardiness and
taking the problems booklet outside the building (particularly to Fort
William). Messrs Bradley, Coggins, Richardson and Monk sat alongside
the chairman, exuding relative bonhomie, as Adam tried to persuade us
that they were the four horsemen of the apocalypse.
We had been given 27 questions by the problems group, and we had to
try them all. I settled down to the task. The problems are divided
into Algebra, Combinatorics, Geometry and Number Theory, and ranked in
order of estimated difficulty. I bravely adopted the horizontal
approach, and tackled each question 1 in turn. I impressed myself by
knocking them over fairly easily, and slept soundly. After breakfast
of haggis (a food substitute) I settled down to try the question
2’s. This is where I came a cropper, and spent a difficult morning
achieving rather little, though now I did recall the talk of having
some particularly easy questions for the weak students. That explained
my prowess of the previous evening. However, after lunch things
started to pick up, and some more of the questions yielded.
In the evening we were given the solutions, and suddenly the
questions looked less intimidating; the benefit of struggling with
them under realistic conditions was clear. The debate on the selection
of the problems raged for a couple of days. We first selected the
harder questions. One was a mixture of geometry and combinatorics, and
the other a fusion of algebra and number theory. After that we
selected a pair of relatively easy questions. I fought hard to stop
the question which was eventually to become Problem 1, producing a
solution only one line longer than the question in an attempt to
undermine its support. This plan narrowly failed. The question was so
easy that the co-ordinators made it a very technical problem in order
to give it some value as a discriminator. It is one of those questions
where almost any method works, so the marking scheme was quite
savage. A momentary lapse would be punished by the loss of four
marks. In fact this played into the hands of the well trained
students, and created major problems for the less well prepared. Later
one of our students was to fall victim to this trap. It cost Tim
Austin a gold medal.
The other easy question seemed rather good. The middle difficulty
pair was fit for the purpose, but a bit too easy in my opinion. The
jury nearly chose an even more beautiful geometry question than the
one they selected for Problem 2. The English Language committee
produced a refined wording of the questions. As UK leader I had to
present this polished wording to the jury. Of course all jury members
are fluent English speakers, so the jury made a lot of subsequent
revisions.
Here are the questions:
First Day
-
Let n be a positive integer. Let
T be the set of points (x, y) in the
plane where x and y are non-negative
integers and x + y < n. Each point of
T is coloured red or blue. If a point (x,
y) is red, then so are all points (x', y')
of T with both 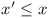 and
and 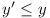 . Define an X-set to be a set of
n blue points having distinct
x-coordinates, and a Y-set to be a
set of n blue points having distinct
y-coordinates. Prove that the number of
X-sets is equal to the number of
Y-sets.
. Define an X-set to be a set of
n blue points having distinct
x-coordinates, and a Y-set to be a
set of n blue points having distinct
y-coordinates. Prove that the number of
X-sets is equal to the number of
Y-sets.
-
Let BC be a diameter of the circle 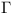 with centre O.
Let A be a point on
with centre O.
Let A be a point on 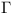 such that
such that 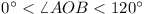 . Let D be the midpoint of the
arc AB not containing C. The line
through O parallel to DA meets the
line AC at J. The perpendicular
bisector of OA meets
. Let D be the midpoint of the
arc AB not containing C. The line
through O parallel to DA meets the
line AC at J. The perpendicular
bisector of OA meets 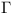 at
E and at F. Prove that
J is the incentre of the triangle
CEF.
at
E and at F. Prove that
J is the incentre of the triangle
CEF.
-
Find all pairs of integers 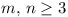 such that there exist
infinitely many positive integers a for which
such that there exist
infinitely many positive integers a for which
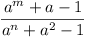
is an integer.
Second Day
-
Let n be an integer greater than 1. The
positive divisors of n are d1,
d2, ..., dk where
1 = d1 < d2 < ... < dk =
n.
Define D = d1d2 + d2d3 + ... +
dk-1dk.
- Prove that D < n2.
- Determine all n for which D is
a divisor of n2.
-
Find all functions f from the set 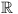 of real numbers to itself such that
of real numbers to itself such that
(f(x) + f(z))(f(y) + f(t)) = f(xy - zt) +
f(xt + yz)
for all x, y, z,
t in 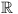 .
.
-
Let 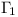 ,
, 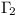 , ...,
, ..., 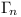 be
circles of radius 1 in the plane, where
be
circles of radius 1 in the plane, where 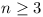 . Denote their centres by
O1, O2, ..., On
respectively. Suppose that no line meets more than two of the
circles. Prove that
. Denote their centres by
O1, O2, ..., On
respectively. Suppose that no line meets more than two of the
circles. Prove that
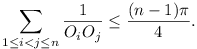
Problems 1 through 6 were submitted by Columbia, (South) Korea,
Romania, Romania, India and Ukraine (respectively).
We were bussed to Glasgow for the opening ceremony. I saw the team
but they did not see me. Naturally we were entertained by a
bagpiper. More surprisingly, an Australian juggler named Colin Wright
gave a dazzling performance. The leader of Poland described him as
“the remarkable man with three balls”.
Next day the students had their first exam and the jury was
entertained by the students’ queries. Happily for the documentary crew
and public entertainment in general, one was from our very own Jenny:
“Am I missing something or must all the points be red?”. I pointed out
to the jury that this was a disjunction and the first clause was true,
so that the correct answer to the question was yes. I craved the
jury’s permission to write “Read the question again!”, and was allowed
so to do. That evening the scripts were distributed quite late, and
there was hardly time to look at them before falling asleep.
After the questions next morning the jury boarded coaches to meet
the students at the end of the second paper. I met the students only
briefly before we became separated, and then we failed to have lunch
together thanks to some dim planning in the restaurant. After being
away from the team for so long I was very angry that I did not have
the chance to talk to them properly. The students vanished and Richard
and I were left to mark. Initially things looked quite good, but after
a while it became clear that Nathan’s script was a traffic
accident. The scripts of Paul, Tim, Jenny and Tom all contained lots
of good stuff, and there were heart-warming moments in Gavin’s
work.
Only Tim had made even minor progress on Problem 6, and no-one had
made more than a little dent in Problem 3. However, the relatively
easy problems had been done rather well by many of the UK team, and
this served to validate the training effort. We had swept up lots of
geometry marks from Problem 2, often using trigonometric formulas
learned for this very purpose.
The Results
The dramatic moment of the co-ordination phase was when Richard and
I believed (correctly) that the cut-off for gold would be 29 and that
Paul Jefferys had solved the remaining two questions completely, and
so would be on 29. There was a slight niggle in that one could argue
that he had paid insufficient attention to a detail in a geometry
proof, and might get only 6/7 for that. My heart sank when I sat down
to co-ordinate that question because the South Koreans who were
running the show had written their proposed scores in their own
language on a pad. I could see that they were proposing to give the
same squiggle to Paul as to Jenny. Since Jenny’s solution was a clear
6/7 we were in trouble. When it came to the script, Richard and I made
out a clear case as to why it should be 7/7. The case was strong
enough for the Koreans, who nodded in agreement that 7/7 was
justified. For a moment we relaxed, yet the gold was snatched away by
the (British) co-ordinators, who argued that it was case law that
Paul’s script was worth 6/7. We acted astonished, and adjourned to
paw over the script looking for further evidence. However, it was not
there, and the gold medal slipped away. This was a great
disappointment, but serves to illustrate the scrupulous fairness and
quality of the co-ordination team.
Tim Austin was also very unlucky to miss out on a gold medal. His
sin was correctly to dispose of infinitely many base cases of a
structural induction. He messed up one easy case, and was fined 4
marks. There were well rehearsed arguments as to why this was just,
repeated ad nauseam. I do not find repetition a very persuasive
argument, and still think that a fine of 1 mark would have been
appropriate (with the more severe penalty for those who failed to deal
with infinitely many base cases). Anyone who thinks that they can
counter this position by rehearsing the standard argument wheeled out
in Glasgow had better seek a career in politics rather than
mathematics. I really did understand first time, and hearing it again
and again does not help. The only argument which has real force is
that the marking scheme mugged everyone in the same way, provided that
they were unlucky enough to use one of the induction arguments with a
delicate base case.
Tom and Jenny were also very unlucky to fall short of the silver
medal threshold. In their cases it is the sheer proximity of the
silver borderline which is so annoying. Gavin has been improving all
year, and to have him stumble at the IMO was a surprise. Those of you
who know Nathan will realise that he is a far stronger mathematician
than these IMO marks would suggest. He is determined to harness his
remarkable talent to much greater effect in the future.
The marks were as follows.
| Q1 | Q2 | Q3 | Q4 | Q5 | Q6 | Total | Medal |
|---|
| Paul Jefferys | 7 | 6 | 1 | 7 | 7 | 0 | 28 | Silver |
| Tim Austin | 3 | 7 | 1 | 7 | 7 | 1 | 26 | Silver |
| Tom Coker | 7 | 6 | 0 | 7 | 2 | 0 | 22 | Bronze |
| Jenny Gardner | 6 | 6 | 0 | 7 | 2 | 0 | 21 | Bronze |
| Gavin Johnstone | 6 | 0 | 1 | 4 | 1 | 0 | 12 | |
| Nathan Bowler | 3 | 1 | 1 | 1 | 1 | 0 | 7 | |
A gold medal was available for 29 points, a silver for 23 points,
and a bronze for 14 points. Thus 9 extra marks, correctly distributed,
would have secured two gold medals, two silvers and a bronze! However,
it was not to be this year. Uncharacteristically ragged performances
from Gavin and Nathan had the effect of depressing our position in the
national rankings. If these two had each secured 20 marks (well within
their capabilities almost all the time), then the UK total would have
increased from 116 to 137 and our ranking would have been
14th rather than 27th.
The leading teams were: China 212, Russia 204, USA 171, Bulgaria
167, Vietnam 166, (South) Korea 163, Taiwan 161, Romania 157, India
156 and Germany 144. Only three students secured full marks (42). Two
of these students were from China and one was from Russia. There was
then a clear gap to a group of six students on 36 points. A student
from New Zealand managed the stunning feat of securing a gold medal
with 29 marks despite scoring 0 on the easiest question (Problem
1).
The UK was near the bottom of a close pack of moderately successful
teams. There was a clear break between the 30th team (Singapore) on
112, and the 31st team (Argentina) on 96. There were 17 countries in
the narrow range 112 through to 135 inclusive.
The monotonic decline in UK scores and ranking since 1996 has been
halted and reversed. Our medals in 2002 were all strong, towards the
top of the range. Four of the team are available for selection in
2003: Nathan Bowler, Jenny Gardner, Gavin Johnstone and Paul Jefferys
will all still be in secondary education next year. Of course the team
selection is not yet made, and these people must compete with other
students who may emerge as leading young mathematicians before IMO
2003 in Tokyo. We are all determined to make the team of 2003 a
serious force.
Conclusion
There were very many people involved in training the UK team this
year, and I thank them all. The performance of the students on the
relatively easy questions is the reward for all that
effort. Christopher Bradley and Adrian Sanders deserve special
acknowledgement for their protracted involvement. Christopher provided
us with a thick wad of geometry questions before he went into purdah
as a member of the problems group. During training the squad always
relished the chance to work on these.
Gavin and Nathan missed out in Glasgow, but have another chance in
Tokyo. Each of them is a very talented mathematician, and stands a
good chance of making the team in 2003. We knew from taking so many
practice examinations that occasionally even very good students can
have a bad exam at IMO level. All the students worked extremely hard,
and the atmosphere in the team was excellent. I am sure that I speak
for Richard and all the other trainers when I say that it was a
pleasure to work with all the students who formed part of the UK squad
throughout the year. This includes those students who dipped in and
out of the squad, all of whom made important contributions both
mathematically and in terms of morale. The achievements of the UK team
in Glasgow must be shared among these wonderful young people. It would
not be appropriate to list all their names, but I will single out
Erica Thompson from Scotland. She was trimmed from our squad after the
FST at Cambridge. She filled the IMO sized gap in her life by getting
selected to represent the UK at both Biology and Physics. She secured
a gold medal at the IBO (coming 5th in the world) in Latvia
and a bronze medal at the IPhO in Bali. In Glasgow the IMO team were
following her progress by text messages from Indonesia (“now we are
going to see a volcano”).
Hannah Burton was a member of the UK IMO team in Washington. Every
team at an IMO gets issued with a guide. Hannah took on that role in
Glasgow, and looked after us very well. The social programme included
excursions for the students, a trip on the Paddle Steamer Waverley on
the Clyde estuary. On the last evening there was a party in a Glasgow
night club (the Arches) which boasted a bucking bronco machine, a
trampoline based game which involved hurling yourself upside down at a
velcro wall wearing a sticky suit, and music played at volumes beyond
the threshold of pain.
The IMO in Glasgow was a splendid event, and the new team uniform
simplified dress issues at the ceremonies. The team met the Princess
Royal in person, and each received a letter of support from the Prime
Minister. Naturally the organization of such a large competition as
the IMO places immense stress on the key organizers, but from the
outside this was invisible. Angela Gould, Adam McBride, Peter Neumann
and Robert Smart and their key advisers and assistants are to be
congratulated on running such a marvellous event.
Return to IMO Register home page
Contact: Joseph Myers
(imo-register@imo-register.org.uk)
Online HTML version last updated:
5 January 2016
![]() and
and ![]() . Define an X-set to be a set of
n blue points having distinct
x-coordinates, and a Y-set to be a
set of n blue points having distinct
y-coordinates. Prove that the number of
X-sets is equal to the number of
Y-sets.
. Define an X-set to be a set of
n blue points having distinct
x-coordinates, and a Y-set to be a
set of n blue points having distinct
y-coordinates. Prove that the number of
X-sets is equal to the number of
Y-sets.![]() with centre O.
Let A be a point on
with centre O.
Let A be a point on ![]() such that
such that ![]() . Let D be the midpoint of the
arc AB not containing C. The line
through O parallel to DA meets the
line AC at J. The perpendicular
bisector of OA meets
. Let D be the midpoint of the
arc AB not containing C. The line
through O parallel to DA meets the
line AC at J. The perpendicular
bisector of OA meets ![]() at
E and at F. Prove that
J is the incentre of the triangle
CEF.
at
E and at F. Prove that
J is the incentre of the triangle
CEF.![]() such that there exist
infinitely many positive integers a for which
such that there exist
infinitely many positive integers a for which![]()