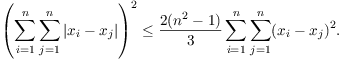~masgcs`
University of Bath
July 2003

Introduction

The International Mathematical Olympiad is an annual competition which takes place in a major city each July. Six students from each country are allowed to take part in what amounts to the World Championships of Secondary School Mathematics. Students are disbarred from the competition either by entering full-time tertiary education, or reaching the age of 20. At most half the students receive medals, and these are awarded in the best possible approximation to the ratio gold:silver:bronze = 1:2:3.

There are two examination papers sat on consecutive days. Each paper lasts 4 hours 30 minutes, and consists of three questions. The first is hard, the second is unbelievably hard, and the third is more or less impossible. Each question is marked out of 7, according to a brutal marking scheme. The least imperfection will lose a mark, and an incomplete solution will usually be rewarded with no more than 2 marks, even for significant progress. This is an event where every mark has to be earned.

As well as the six students, teams usually send along at least two adults. One is the leader, and his or her role at the IMO is to sit on the jury. There is also a deputy leader who stays with the team and looks after them. In the UK we are very fortunate in that the current deputy leader is Richard Atkins of Oundle School, the director of the national mentoring scheme. Richard also helps with training. This year he was accompanied by Adrian Sanders of Trinity College, Cambridge, who will succeed him as deputy leader.

The UK team is selected from a squad of students who are preparing for the event. Students are invited to join the squad by virtue of excellent performances in national mathematics competitions, normally BMO1 and BMO2. The training schedule is designed to have minimal impact on normal school work.

The Results of IMO 2003

The questions chosen by the jury for the 44th IMO were as follows.

Let A be a subset of the set S = {1, 2, ..., 1000000} containing exactly 101 elements. Prove that there exist numbers t₁, t₂, , t₁₀₀ in S such that the sets

$A_j = { x + t_j | x \in A } for j = 1, 2, ..., 100$

are pairwise disjoint.
Determine all pairs of positive integers (a, b) such that

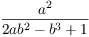
is a positive integer.
A convex hexagon is given in which any two opposite sides have the following property: the distance between their midpoints is 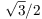$\sqrt{3}/2$ times the sum of their lengths. Prove that all the angles of the hexagon are equal.

(A convex hexagon ABCDEF has three pairs of opposite sides: AB and DE, BC and EF, CD and FA.)
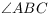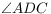Let ABCD be a cyclic quadrilateral. Let P, Q and R be the feet of the perpendiculars from D to the lines BC, CA and AB respectively. Show that PQ = QR if and only if the bisectors of $\angle ABC$ and $\angle ADC$ meet on AC.
Let n be a positive integer and x₁, x₂, ..., x_n be real numbers with .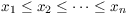
1. Prove that
  
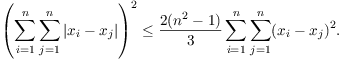
  $( \sum_{i=1}^n \sum_{j=1}^n |x_i - x_j|)^2 <= (2(n^2-1)/3) \sum_{i=1}^n \sum_{j=1}^n (x_i - x_j)^2.$
2. Show that equality holds if and only if x₁, x₂, ..., x_n is an arithmetic sequence.
Let p be a prime number. Prove that there exists a prime number q such that for every integer n, the number n^p - p is not divisible by q.

If you manage to solve any of them, especially the tough question 3 or 6, please send your solution to me (address below).

The breakdown of the UK marks is as follows:

                  Q1  Q2  Q3  Q4  Q5  Q6      Total

Nathan Bowler      7   3   0   5   1   1       17
David Fidler       7   3   0   7   0   0       17
Jenny Gardner      7   7   0   7   7   0       28 
Paul Jefferys      7   7   0   7   7   1       29
Gavin Johnstone    7   3   0   7   1   0       18
Martin Orr         7   3   0   7   1   1       19

As a result of these marks, the team were all awarded medals.

Paul Jefferys       29 Gold   (Berkhamsted Collegiate School)
Jenny Gardner       28 Silver (Tiffin Girls School)
Martin Orr          19 Silver (Methodist College, Belfast)
Gavin Johnstone     18 Bronze (Dame Alice Owen’s School)
Nathan Bowler       17 Bronze (Knutsford High School)
David Fidler        17 Bronze (Haberdashers’ Aske’s School)

The cut-offs were 13, 19 and 29.

Although the IMO is an individual competition, just as in the other Olympics, it is an unofficial habit to rank the performances of nations using total team scores. On this basis the United Kingdom came in equal 10th place, recovering from 27th in 2002 and 31st in 2001. Here are the marks of the 44th IMO of those countries scoring 90 marks or more.

1 Bulgaria 227, 2 China 211, 3 USA 188, 4 Vietnam 172, 5 Russia 167, 6 Korea 157, 7 Romania 143, 8 Turkey 133, 9 Japan 131, 10= Hungary, United Kingdom 128, 12= Canada, Kazakhstan 119, 14 Ukraine 118, 15 India 115, 16 Taiwan 114, 17= Germany, Iran 112, 19= Belarus, Thailand 111, 21 Israel 103, 22 Poland 102, 23 Serbia & Montenegro 101, 24 France 95, 25 Mongolia 93, 26= Australia, Brazil 92, 28= Argentina, Hong Kong 91.

These were the best performances among the 82 nations which participated. Observers were also present from Mozambique and Saudi Arabia, so those nations may participate in IMO 2004 in Greece. Those of you who are interested in more IMO statistics may enjoy visiting Joseph Myers’s site http://www.srcf.ucam.org/~jsm28/imo-scores/

Before addressing parochial concerns, it is appropriate to note with respect the astonishing performance of Bulgaria. Their lowest mark was 34, and on the two hardest questions they obtained 11 scores of 6 or above. The population of Bulgaria is 7.6 million and its GDP is 1/30th that of the United Kingdom and 1/120th that of China (population 1248 million). Their performance is no flash in the pan; they last slipped out of the top 5 in 1997.

Now for some navel-gazing. The United Kingdom has, at least for one year, regained the sort of form it displayed in the early and middle 1990s. To look on the bright side, the UK managed to get the most marks of any country in the European Union or the Commonwealth. We also managed to do better than any successor state to the USSR save for Russia itself. The tie with Hungary is a particularly happy chance, since we train with them every winter and they are therefore our closest friends in the competition.

Every UK student obtained a medal, and the marks of each UK student were in the top 30%. Paul Jefferys obtained our first gold medal since 1997 (by one mark), having failed to do so last year (by the same margin). Jenny Gardner was the 5th placed girl in the world, and missed the gold cut by a squeak. She was actually ranked equal 38th. Martin Orr’s silver medal is the best performance ever by a UK student resident in Northern Ireland. No student representing the Republic of Ireland has won a gold or silver medal so far, so Martin is top of the all-Ireland list. Our three bronze medals were all very strong, and the least bit of good fortune could have tipped any of them into the silver zone.

We had three very strong reserves in Bryn Garrod, Alex Davies and Paul Smith. Each one of them had every hope of making the team, and moreover it is extremely likely that each of them would have obtained a medal if he had been selected. Alex is available for selection in 2004.

Note that the foundation of the UK score is 82/84 on the relatively easy questions 1 and 4. In fact only China and the United States managed to do better on these two problems. On the other hand, our performance on questions 3 and 6 was dismal (as it was in 2002). The way forward for the team is to try to consolidate our performance on 1 and 4, to try to match it on 2 and 5, and to do better on 3 and 6. Note that a perfect score on questions 1,2,4 and 5 would alone have produced 6 silver medals, and would have beaten Russia into 5th place by one mark.

The performance in Glasgow 2002 (UK ranking 27th) was better than it looked, because we were breathing down the necks of lots of other good teams. However, one must worry that the performance in 2003 owes something to chance; it is unlikely that all six students will solve (or almost solve) all the easy questions every year. Even the mighty Bulgarians did not manage it in 2003.

The year 2002–2003

The 43rd IMO in Glasgow in July 2002 put the resources of the United Kingdom Mathematics Trust under considerable strain. It is a tribute to all concerned in the organization of the event that from the point of view of outside observers it seemed a model of planning and efficiency. The frantic improvisation and the resort to desperate emergency measures (essential for any event on this scale) remained hidden from view. It was not a financial disaster, all the kids got home eventually, and one or two organizers are still on speaking terms. If future IMO hosts can match this, they will be doing well.

While the rest of the British mathematics enrichment community went into post-trauma therapy, we had to get the UK preparations for IMO 2003 under way. We began with a camp in September at the University of Bath. This was a gentle event, mixing returning students with newcomers. We began our mentoring scheme. There are several levels of this scheme in the UK, the one relevant to the IMO being the Advanced Scheme. The deputy leader Richard Atkins is the overseer of these schemes, and the Advanced Scheme was run by Michael Ching of the Massachusetts Institute of Technology. I also send out a couple of mock IMO papers every month for the IMO squad to administer to themselves.

At the turn of the year the squad went on tour to Hungary for our annual joint camp with Sandor Dobos (the names commute) and the Hungarian squad. This is administered by the Bolyai Society. This camp really deserves a report all by itself. In the morning we had lectures by various Hungarian experts, and in the afternoon the students worked on problems and presented their solutions before supper. For the second year the camp was held in a rambling boarding school. A minor defect of the current arrangement is that some of the Hungarian students who live in Budapest tend to slip home in the evenings. By agreement with Sandor the next camp will be held in an academic hotel on the Danube in the beautiful Hungarian countryside. This will bring the students even closer together. We have been approached by the leader of the Luxembourg IMO team to ask if he may come and bring one or two students in the future. This seems very likely to happen.

In the Spring the results of our most advanced national mathematics competitions (BMO1 and BMO2) came in, and we used the information to inform our selection of 20 students to attend a camp at Trinity College, Cambridge. I rather enjoy the marking week-end for BMO1 which has been held at Egham in recent years.

Hitherto the Easter Trinity College camp has unified, but this time we split it into two streams for less and more experienced students (‘mint’ and ‘used’). We had at least one joint session every day, but otherwise the two groups worked most of the time separately. As usual we were completely overwhelmed by offers of help, and it is this rich supply of talented coaches that gives us the option of holding so many parallel sessions. Selecting the final 9 for the intense training period was as tough as ever, and we hope that we made the right choices. This is not an exact science.

The correspondence course is fairly intense, but sharing the marking with Richard and Adrian lightens our load. In all honesty it doesn’t help the students very much. In late May we had a camp at Oundle School near Peterborough, and selected the final team of six and the three reserves Alex Davies, Bryn Garrod and Paul Smith. Leaving out these three excellent young mathematicians was not an easy decision. The last place was completely open right until the Oundle Camp where David Fidler displayed flashes of brilliance which secured him a berth.

We had hoped to have a pre-IMO camp in Hong Kong jointly with the team from the special administrative region en route to Tokyo, but unfortunately the SARS epidemic had been at its height at the time when it was appropriate to book tickets, and following UK government recommendations, we had no choice but to cancel that camp. Our students were very disappointed, and I would like to take this opportunity to thank the Hong Kong mathematics enrichment community for their help and understanding.

The motivation for having a final camp in Hong Kong was longitude training. We wanted the team not to be suffering from jet-lag during the IMO. We therefore sought somewhere in a time-zone close to that of Japan, and somewhere fairly hot to mimic a Tokyo summer. A glimpse at the map and a suggestion from Tony Gardiner were enough. We headed for tropical Queensland. Our hosts were to be James Cook University, which has a small campus in Smithfield (good name) in a northern suburb of Cairns. The financing of all this was possible because JAL were offering very cheap return tickets from London to Australia, with the option of a stay in Japan on the return leg.

To get the flavour of IMO 2003, I will follow the usual practice and present a personal IMO diary. Of course this is only one perspective, and the students’ experience will have been very different.

Leader’s Diary IMO 2003

June 28th Seven of us gather at Heathrow; two more (Adrian and David) will fly tomorrow. We all have JAL flights, but my party’s tickets have been re-routed via Paris. The flight there is easy enough, but the flight on to Osaka is horrible. Richard and I have piecewise rigid legs (obviously it is easier to fold students). We are unable to obtain seats with proper legroom, and by the end of the 12 hour flight neither of us is a happy bunny.

June 29th We arrive in Osaka airport Sunday lunchtime. The team is mostly fine but we seniors are used and bruised. Happily the airport is virtually deserted. Many of us have showers in the executive pampering zone, but frugality dictates that we spare ourselves the vibro-massage chairs. We eat a decent Japanese lunch after pointing at plastic models of the meals. It is now clear that the party will divide into two schools, those who embrace and those who are suspicious of alien cuisine. Gradually we all turn human. Osaka (near Kobe) airport is built on an artificial island. Apart from that there is not a lot to be said.

The cabin staff on the flight from Paris were so anxious about Richard and myself that they phoned the check-in desk for our Australia bound flight to reserve us seats by the emergency exits. We were very grateful, but happily the flight south is on a nearly empty jumbo, so everyone is able to stretch out and relax.

June 30th We arrive at dawn in Brisbane. There is a minor crisis when immigration go sour on my admittedly very beaten-up passport. They are squaring up to bounce me from entry when it dawns on them that this will cause an international incident. I grovel, and they let me in ‘just this once’. We take a hotel shuttle bus to our hotel, the Royal on the Park. We are only going to be in Brisbane overnight, so I have reserved rooms in a fairly luxurious hotel. This is a very popular move as the mangled remnants of the team need some serious opulence. The hotel let us into our rooms well before they need to, and give us a big discount on a hearty breakfast. We do quite a lot of sleeping and showering that day. In the evening we get up, and stagger 200 yards to an Irish pub-cum-restaurant. This is our first encounter with Xcite pheromone wipes. These are sold in packets and apparently enable the user to attract members of the opposite (or presumably the same) sex. They carry a dour warning message ‘use responsibly’. I decide to refrain from purchasing one of these towels lest I unleash forces that I might be powerless to control.

July 1st Richard decamps to the airport to meet David Fidler and Adrian Sanders. They all arrive back in time for breakfast. Their journey was more comfortable than ours. We offer to book them into the hotel for the day, but they heroically decline. We pack for the evening flight north to Cairns, and go out to play for the day. We spend the morning on a municipal river taxi seeing the riverside of Brisbane. We see southern cormorants with white breasts, and Australian pelicans (which are readily distinguishable from Hungarian ones). At lunchtime I lead a party to Chinatown to eat Lakhsa, the world’s best soup. The less adventurous seek more prosaic cuisine. In the afternoon we stroll in the botanical gardens, then some of us savour extra-large cappucinos called, as they should be in the land of the tortured vowel, ‘muggucinos’.

In the evening all nine of us make for the domestic airport to take a Virgin Blue flight to Cairns. It turns out that brother Branson has his own terminal in Brisbane, and can toy with hapless passengers. We hear an announcement ‘Ladies and gentlemen; boys and girls’ it began, in a bouncy tone familiar to those who watch commercial television channels on Saturday evenings. At first it was a joke, and then it became a major irritant. Everything was prefaced by this phrase. Never mind the passengers, how do the staff put up with it?

The flight only lasts a few hours, during which time one or two male members of the team fall in love with the help. If you want to be there, try an Australian setting of “A Subaltern’s Love Song” by John Betjeman.

We arrive in deep midwinter in tropical Queensland. It is dark and 8pm. The Student Lodge has promised to meet us with transport. Richard and I scour the airport for our bus without success, as cicadas mock our plight. Telephone calls to the Student Lodge yield invitations to leave messages on their telephone answering machine. We are in trouble. We decide to gamble and take a maxi-taxi (with all 9 and our luggage) out to the suburbs and the Lodge. If it is deserted we will have to go to the centre of Cairns and find a hotel.

We find reception in deepest murk. We leave Adrian with the team and go wandering through the student accommodation. We find a resident tutor and explain the situation. She rolls her eyes in embarrassment. We deduce that this may have happened before. She quickly rounds up other tutors and they prepare rooms for us. It is very late, but a pizza parlour is nearby. Richard and Adrian obtain an excellent dinner for the team, and so to bed.

July 2nd We awake to consider our position. The accommodation is Spartan but acceptable. After breakfast I am introduced to the administrator. It takes her some time to realise the extent of her mistake. She formally apologizes to me in Queensland fashion; this does not involve the use of the word ‘sorry’ but she does acknowledge that ‘I really stuffed up’. Well, I remain calm, polite and friendly. From that moment on our host became extremely helpful indeed, and made our stay at the Lodge a very happy experience.

David Godwin of the Mathematics Department of James Cook University has arranged for us to have use of a beautifully cool room for our daily exams. At first we are a little surprised at his apparently eccentric room reservation methods, which seem to involve being a personal friend of every security guard on campus. Later we have reason to have a minor tangle with the official procedures of the university, and realise the wisdom of David’s technique.

July 3rd–6th We spent this time doing mathematics, save for an excursion to the Great Barrier Reef by catamaran. Richard prepared a laminated geometry problem sheet which the team could work on while snorkelling. There were also trips in a glass-sided semi-submersible boat, and I was lucky enough to see some turtles from this vessel. Gavin and Martin looked a little the worse for wear after their snorkelling sessions, but recover quickly.

Mathematical preparations were proceeding apace, but after a couple of papers where the team did very badly, we substituted some easier questions on the next paper in an effort to build up their self-confidence. I had to fly off to Japan on July 7th, leaving the team in the capable hands of Richard, and the deputy-in-waiting Adrian Sanders. Adrian is a former IMO team member, and very strong mathematically. He will be a great deputy leader, though Richard will be a hard act to follow.

July 6th I fly from Cairns to Brisbane, and stay in a hotel near the airport. It is a last chance to savour Australian Thai cuisine.

From now on I am out of touch with the team, but I feel that I should pass on the details of an incident which happened after I left. Adrian and Richard were conducting an algebra session, and while the students were working on the problem sheet, Adrian adopted that inscrutable reflective pose which Cambridge people use in an attempt to convey the impression of wisdom. Time passed, until Richard realised that Adrian was in fact asleep. Richard proceeded to round up the session in Adrian’s intellectual if not actual absence. Richard is an experienced Head of Department, so he is used to this sort of thing.

July 7th The flight north to Tokyo is easy enough. Japanese immigration are not fussed about my scruffy documentation, and become very friendly when they discover the IMO connection. I reach the arrivals area mid-afternoon to be greeted by Tokyo IMO apparatchiks. The next bus will be at 6:30pm in a couple of hours. I see old friends the leaders of New Zealand, and Spain, and am introduced to some other leaders. The secretary of the IMO Advisory Board, John Webb, has arrived from South Africa, but his luggage has been lost in transit. I sympathize and recount how Austrian Airlines recently managed to lose my luggage three times in two weeks (allowing stuff to be nicked in the process). It seems that both Dubai and Vienna are luggage transfer black spots. Be warned.

The 90 minute bus journey across Tokyo in the dark is impressive. There are towers, Ferris wheels, overpasses, underpasses, middlepasses and giant posters of David Beckham. It goes on and on. Eventually we reach the National Olympic Memorial Youth Centre, a complex of student accommodation and teaching buildings near Shinjuku in the heart of Tokyo. At last I get my hands on the problems shortlist, with no answers provided. My room is tiny by Western standards, but air-conditioned and I have my own bath (rather like a top-loading washing machine without a lid). It is fine. I go to bed to enjoy the problems.

July 8th–10th At breakfast I walk in to a sea of friendly faces. The leaders are gathered. It is my duty as UK leader to wage psychological war on other participants, so I elect to use chopsticks (I am proficient). The conversation is all about the shortlist. Of course we haven’t had time to try all the questions yet, but even at this stage some questions have attracted fan clubs and others are clearly headed towards oblivion. I work on the problems all day, and late in the evening we get the solutions. There are some good geometry questions, but the combinatorics section looks weak, and many of its problems are very geometric. The algebra and number theory sections are both quite attractive.

I wonder if any of the UK questions have made the shortlist. As a matter of policy I deny myself the opportunity to see the UK proposals in case it influences my judgement.

The next day is spent in pleasant discussion of the merits of questions, making no apparent progress towards selecting the examination until a critical moment passes and we quickly choose the two harder questions. The Japanese chairman Prof Yuji Ito is very good, taking us forward by gentle coaxing. One is the geometry problem which will become question 3. The problems committee classify it as hard but it doesn’t seem too bad to me. Since the UK will subsequently score 0 on this question, it shows how much I know. The other choice will become Question 6. This is a number theory question which I reckon is simply impossible. The solution seems to be applied magic. There is commentary in the shortlist explaining how one might come across the correct argument by a rational process, but I am far from convinced. The result is pretty, and it seems surprising that such a result can be obtained using IMO methods. It seems like a good question to sort out the top of the rankings, so it gains my support.

We begin to focus on the easier questions. I am pretty sure that a lot of combinatorics questions which are classified ‘medium’ should actually be classified ‘easy’. I know this because I could do them before the solutions were handed out. The jury will not hear of it. I produce and distribute a fast solution to C4, as do several other leaders, but the jury are not persuaded. I quite like the ‘easy’ number theory problem N1. It concerns recurrences, and it is possible to do it in your head. The solution makes me laugh out loud. There is a trick which you have to see or know, otherwise the problem is completely intractable. Apparently this trick has been used in another problems competition, and prior knowledge would give a candidate a fantastic advantage. For this reason this question does not make the final paper. Also, the distribution of marks on this question would have been bimodal. If you see the trick you would get 7, without it 0 would be certain.

We carry on choosing. We select the easier questions. One combinatorics and one geometry. The leader of Poland makes a learned submission as to why G1 and G2 are actually the same question at a deep level, and that in turn are equivalent to a question in a recent Austrian-Polish competition. Close analysis of his arguments persuades me (and the jury) that anyone who makes these connections deserves a gold medal anyway, so he is ignored. We now have a difficulty. We have chosen two geometry questions, and most of the likely remaining ‘medium’ combinatorics questions are highly geometric. We have to pick a ‘medium’ algebra question so we do, an inequality, and a number theory question makes it as the second ‘medium’ question.

When the questions have been chosen the national origins are revealed. They are (in sequence) from Brazil, Bulgaria, Poland, Finland, Ireland and France. The Irish leader and observer are delighted to have a question on the paper. It turns out that no UK problem has made the shortlist this year.

As UK leader I chair the English language committee. There is the problem of the excessive articulacy of the New Zealand leader. I neutralize him by making him the secretary of the meeting. He will be kept very busy making drafts and keeping notes, so that more timorous leaders can have their say. There is also the problem that most leaders think that they can speak perfect English, and some get resentful when the native speakers meet behind closed doors. I solve this by announcing to the jury that only native speakers may attend, but that the definition of native speaker is ‘anyone who would like to be a native speaker of English’ (apologies for the infinite regression). Once the meeting is open to all, attendance ceases to be attractive, and most of the non-native speakers drift away. The leader of Luxembourg, Charles Leytem, attends, but he is an honorary native speaker of everything. We finish quickly, and then I present our proposals to the full jury. I am fatalistically relaxed, because I am expecting our wording to come under fierce attack (because the jury is ahead of schedule and so there is time to fill). In fact we quickly dispose of the English language with very few changes, and then enter into a debate about mathematical notation. I realise that I should really hand the chair back to jury chairman Prof Yuji Ito, but he looks very unenthusiastic and obviously wants me to carry on.

The annual agony over the use of summation notation starts spiralling round without coming to any conclusion. The discussions ramble in an unstructured way. At last I decide that we have to put a lid on this, and I suggest to the jury that we should proceed formally with motions and votes. There is general agreement. I then start applying the rules of order inflexibly, and through a sequence of votes we quickly come to a conclusion. The leader of Bosnia and Herzegovina wants the jury to agree on a standard answer to questions about summation. I suggest to the jury that Bosnia and Herzegovina be put in charge of this and they agree. That takes the edge off the appetite for further suggestions, and the presentation of the English language committee draws to a conclusion.

As I return to my seat the leader of Iran makes a point of order as to whether the leader of the United Kingdom should have been allowed to conduct votes. The jury chairman quickly blows this problem away by asserting that he had delegated the responsibility.

Michael Albert of New Zealand types up the English version with me riding shotgun. It is then distributed to the leaders responsible for the official IMO languages (French, German, Russian and Spanish). It turns out that there is a problem. No standard template has been defined and everyone is making up their own. It is a nightmare. I meet with the leader of Spain and agree a format. We tell the leaders of France, Germany and Russia. Everyone agrees but France ignores the agreement (plus ça change). In the interests of world harmony we all swap to the French notation (it involves the use of bold type in a certain place). The official versions are then duplicated and the translations into all the other languages can begin.

July 11th The students are arriving today. The leaders must be taken away for security reasons. We are allowed to leave belongings in our rooms at the Centre, which is very convenient. We have a two hour drive across town and round the bay to the Makuhari hotel. This pleasure palace is 25 floors high and fairly swish. I have a room on the 10th floor which is far from large by Western standards, but by comparison with the previous accommodation it seems huge. We have meal vouchers, which is a good idea because the restaurant prices are high.

Finally there is a presentation by the co-ordinators (the marking police) of what they plan to use as a marking scheme. Mostly it is fine but in a couple of places there are major problems. It is a political matter to persuade the co-ordinators that they are wrong, and to allow them to make changes without loss of face. This is accomplished without too much blood on the carpet, with the chair of the IMO Advisory Board and Hungarian leader József Pelikán playing the tough cop to Michael Albert’s soft cop.

July 12th We are taken back to the Youth Centre by bus in order to attend the opening ceremony which is mercifully short. Together with the other leaders I am required to enter the theatre via the stage, passing in front of giant drums being frenetically beaten by Japanese dervishes. The UK team look great. They are in their uniform and look menacingly professional. I hope this has an unsettling effect on some other teams. The leaders are taken back to the Makuhari hotel without contact with the teams. The final marking scheme is agreed. It is now significantly improved. The co-ordinators are doing a great job. I make a speech thanking them for their reasonableness in a pathetic attempt to curry favour.

July 13th The first exam. The leaders meet at 9am in a room near a bank of faxes. Students are allowed to ask their leader questions during the first thirty minutes. These are transmitted by fax to the leaders’ site. Each leader presents their question to the jury, and proposes a reply to be sent back by fax. The first question arrives. My heart sinks. It is from a United Kingdom student. Paul Jefferys wants to know if he can assume the truth of the Axiom of Choice. I don’t want to cramp his style, so I propose the answer ‘yes’. Paul’s question causes general hilarity in the jury room. The leader of France, Claude Deschamps, rushes up to me in delight “so the UK has adopted the conventions of Bourbaki!” A happy time is spent addressing more serious questions, most of which concern the meaning of the phrase ‘pairwise disjoint’.

In the evening there is an excellent banquet, and then the scripts arrive. This is a telling moment. I read the scripts carefully, and to my delight I can’t find anything wrong with any answers to Question 1, and both Jenny and Paul seemed to have done Question 2. The solutions to Question 3 are not very impressive. Paul has some calculations and Jenny has some ideas.

July 14th The jury meets at 9am for the questions associated with the second exam. I brace myself for another Paul Jefferys special, but it doesn’t come. Instead we have a predictable time answering questions about summation notation. The final question of the morning is from Gavin Johnstone. It has two parts. Firstly he asks a nervous question about the meaning of ‘angle bisector’ (can the bisector be of an external angle), and secondly he points out that his exam started late, so he wants to know if lunch will still be available when he comes out. By now the jury is demob happy, and some clown suggests that I write ‘read the question again’ in response to his final query. I point out that ‘have your breakfast again’ would be more helpful.

The leaders then depart from the hotel, and race across town to the exam site. As the students finish their second paper we wait for them to come out. All our students are claiming to have solved Question 4, and both Jenny and Paul are also staking a claim to 5. If they are right, then each of them will be close to a gold medal and the whole team should have medals (fingers crossed).

There are some rooms set aside for marking, but we find them excessively noisy so the UK seniors set up camp elsewhere. A careful reading of the scripts indicates that the students are more or less accurate in their claims. Question 1 definitely looks like 42/42 for the UK and Question 4 looks like 35/35 plus whatever Nathan’s script is worth. He has used a method so bizarre and baroque that beyond our confidence in him, we are not at all sure if he is right. Faced with a problem about a cyclic quadrilateral, he begins by considering a non-cyclic quadrilateral, inverting with respect to a circle of Apollonius (which he calls a circle of Menelaus in order to add colour) and then concludes with an argument which views a cyclic quadrilateral as a limit of an infinite sequence of non-cyclic quadrilaterals. Each step of the argument is justified with a helpful note such as “by a standard result of inversive geometry”. It is a nightmare. Initially Adrian and Richard devote themselves solely to this one question in Nathan’s script while I work on the other 35 solutions. I definitely have the easier job. They spend the day trying to understand Nathan’s arguments, and get progressively more stressed about what happens to directed angles under inversion. I discover that all the other Question 4 solutions are fine, except possibly for Paul’s which is a long and cunning trigonometric slog. I push that over to Adrian and Richard, and go hunting for scraps among the fragmentary solutions. I get more and more excited about Question 2. Unusually up to 3 marks are awarded for noticing various specific things. As I dig through the four non-solutions from David, Gavin, Nathan and Martin I keep on finding nuggets worth marks. Each one of them, tucked away in odd corners of reasoning, has made enough of the correct observations to get all 3 marks. I am purring. After last year when everything fell to bits I am very nervous, but this time it looks as though things are going our way. Provided Nathan’s foray into inversive fairyland is not complete nonsense, and he picks up at least a couple of marks for it, then everyone should get a medal. Question 6 is also interesting because a legalistic reading of the marking scheme would give us 4 marks distributed across four members of the team. This would be absurd, but mathematicians are very literal, so there is hope.

Sustained reading of Nathan and Paul’s solutions to Question 4 is clearly a health hazard, so from time to time Adrian and Richard refresh themselves by looking at other solutions. We are all cross-checking one another, making sure that at least two of us are expert on any given page of writing.

July 15th We begin co-ordination at 9:00am. This is Question 6 and we have our legalistic hats firmly on. When we explain our case, the co-ordinators laugh (quite rightly). We act serious, and tell them that the marking scheme must be adhered to strictly. They laugh again. Right we say, if you are not giving us the marks for this, make sure no-one else gets them either. Please write this position up on the board (Adrian’s excellent suggestion). Looking at the board, we see that another notice is already there. It says that a certain observation is worth 1 mark. We say that this is new and that we have not searched for this observation. The co-ordinators have looked, and together we find 3 marks, 1 each for Martin, Nathan and Paul. This mark for Paul is crucial, because with four relatively accessible questions and two hard ones, the gold cut-off may well be 29. The mark for Martin is also vital, because it will later tip him over the silver boundary.

Later in the day we co-ordinate Question 4, the ‘easy’ geometry one. Four scripts are perfect, and we spend an age justifying Paul’s trigonometry. In the end they can’t find any holes, but they want to sleep on it. We agree to meet next day at 5pm to settle it and to address Nathan’s new age solution. Perhaps it would be easier to follow if we all sat under a pyramid.

In the afternoon we co-ordinate Question 2 on number theory. This is the one where I have been burrowing for marks in the rambling pages. The co-ordinators begin by giving us a form, asking us what marks we want and why. We ask for two 7s and four 3s. First we look at the partial answers. On each occasion we are asked to show exactly where the key observations were made. I have the list of locations in front of me so we quickly gather up all the part marks. Next we look at Jenny’s script, which is (as is often the case with Jenny) absolutely perfect. She gets her 7. Now for Paul. The story behind this is that Paul had only solved the problem close to the end of the time, and wrote it up in a frenzy. Our position is that the solution is all there, and that even though some of the bends are taken at speed, he deserves 7 marks. This takes some debating, and Adrian is particularly good at explaining why it was worth 7. He was a co-ordinator in 2002 and had seen similar scripts get 7 then. The Japanese co-ordinators are finally persuaded, and offer 7. At this moment Titu Andreescu steps in, the ex-US leader and advisor to the jury chair. He tries to persuade any Japanese he meets that he is in Tokyo to study Sumo. He suggests Paul’s script is only worth 6 with a twinkle in his eye (quite a terrifying sight in fact). The problem captain over-rules him and Titu backs down smiling (equally disturbing). Paul has scraped a 7.

July 16th The morning co-ordination is Question 5, the inequality. By now intelligence reports have reached us that a clever re-arrangement of the left hand side is worth 1. Excellent, for that is more free marks. The only person to score 0 here is therefore the unlucky David Fidler. As usual Jenny’s solution is beautifully clean. Paul’s answer is a little grubby but it is all there. Once again he gets a 7.

The lunchtime co-ordination is of Question 3, the hard geometry. We try to sell Paul’s first line and Jenny’s ideas as being serious progress in the problem. The co-ordinators smile and say no, very politely, and we get six 0s.

By now the agreed marks of the various teams are starting to appear on display, and it is tempting to do furtive calculations. I am delighted since it looks as though we will come in the top 15 countries even if everything goes against us in the remaining decisions, and our rivals do very well. The Irish deputy, Gordon Lessells, is unofficial keeper of the data. He is always the first to know where the cut-offs will be.

I look forward to the afternoon co-ordination of Question 1 because we are sure that we have six 7s. I take the lead in co-ordination, and am surprised that the co-ordinators have some questions about Paul’s script. There is a nasty sinking feeling in my stomach as I worry that they have found a glitch which we missed. Happily Paul’s solution is correct, and the reason for the problem is that they have not understood the precise import of the word ‘until’. All of our solutions are different, but they are all perfect.

It remains to have the final session on the scripts of Nathan and Paul for the Question 4. One (and possibly more) of the co-ordinators has clearly stayed up half the night with these scripts because they now know almost as much about them as we do. We deal with Paul’s first. We deal with a couple of easy points and then they throw us a curve ball. Surely he has only dealt with one configuration when two are possible? I have a speech ready about this, but Adrian nips in with “yes, but he deals with directed lengths as he explains on page 19”. The co-ordinators think, and finally give in. I don’t have to use my prepared tantrum about how when students use a more geometric approach we know that the co-ordinators have let through solutions which do not cover all possible configurations. “Why should the United Kingdom be singled out for punishment when other countries have got away with it? Either give us 7 or mark the question again for everyone!”. Anyway, once again Paul squeaks home with a 7.

As for Nathan’s script, I am hoping that if we address enough of their questions the co-ordinators will give in and deliver a 7. Unfortunately the co-ordinators are too good, and have found the two weak spots in his argument. We put our hands up, and ask for 6. They smile and offer 5. Adrian has long since spread his fingers under the table forecasting 5. We put up resistance, but they are firm. We take the 5, and our co-ordination is complete.

We rush back to the room where information is being displayed. Gordon Lessells pronounces that the gold cut-off will be 29. Paul is incredibly lucky to have crawled over the line, and Jenny is very unlucky to have fallen just short with four immaculate solutions. I think we have 1 gold, 1 silver and 4 bronzes. Our score of 128 marks might put us in about 12th place.

As the results come in, our rivals falter, and in the end we achieve 10th place equal with Hungary. I go to supper, but Richard runs in to say that the silver cut-off is 19. I don’t twig at first, but it means that Martin’s medal is silver not bronze.

Before the final jury meeting the students come back from a trip, and we break the news. Everyone is happy, and even Jenny shows no sign of disappointment. Martin does not seem to believe that he got silver. The leader of the USA, Zuming Feng, is very keen that Jenny should get a gold medal, and starts lobbying to move the gold boundary down to 28. However, the rules are clear and this is quite impossible. I am touched by his thoughtfulness.

The jury meeting is delayed because Taiwan and Turkey are still arguing the toss. Finally they agree their scores and in the end the boundaries are as predicted. The game is over for another year.

July 17th Today the students go to Disneyland, and the leaders go to a temple by bus. I know about buses and the IMO, so I stay in my room and read a PhD thesis to recover from adrenalin poisoning. A sequence of extremely hot baths is just the ticket.

July 18th The day of the closing ceremony. We all wear uniforms, and the students have Union Jacks to display if they wish. Martin declines to be seen with the flag (he is in the Irish team for the Informatics Olympiad, and walks a careful diplomatic path). The ceremony takes place in the presence of the Crown Prince of Japan. The audience is instructed to remain in its seats. This is a disaster from a photographic point of view, so all three UK seniors get up and walk to the front (very disobedient). The ceremony is fine save for some moments of confusion. The students getting bronze and silver medals are required to stand behind the people presenting the medals, so seeing them is hard.

The gold medallists go up about three or four at a time to receive medals from the Japanese answer to Charles Clarke and the Chief Executive of Fujitsu. There is much milling about as all the gold medallists gather on stage, but Paul manages to get to the front of the pack and switches on the smile.

The Crown Prince leaves, and we have to be penned up while he does this, so we go into daytime TV mode. The presenters walk among the audience and ask them questions of limited interest. Each country has a local guide, and they all walked on stage to be clapped. Our guide, Junko is there. She is very skilled at booking hotels and making mobile telephone calls. Her English is very good.

After the ceremony we all mill around outside. Most members of the UK team wear our flag as shawls, and it looks very attractive. Japanese television takes a great interest in us, and Paul is interviewed concerning his opinion of the quality of Japanese girls. He gives the correct answers. Martin is photographed surrounded by the Irish team, and there is a very happy mood. To avoid standing around in uniform Junko leads us across town by metro to the Centre. We change into relaxed clothes for the banquet. The seniors are separated from the teams at the banquet which we don’t like at all.

After the banquet we are led by Junko to a karaoke bar. We have our private room for the UK delegation, Junko and the Swedish guide who has joined us for no apparent reason but she is very welcome. Beer is brought for the seniors. It turns out that Adrian croons a mean ballad. I discharge a long-held ambition and become Grace Slick for 3 minutes. Whether it is Jefferson Airplane or Starship I cannot tell, but the team suffer my rendition of “Somebody to Love”. Most people chip in, but we can’t compete with the duet from Paul and Jenny. Paul has acquired a sash from the banquet which reads “United Kingdom”. Jenny wears this in beauty queen style, diagonally. They sing a perfect rendition of Aqua’s classic “Barbie Girl”. The original is available at http://user.itl.net/~bluecdr/barbiegirl.htm

Barbie Girl

Hi Ken
Do you wanna go for a ride?
Sure Ken.
Jump in.

I’m a barbie girl, in a barbie world
Life in plastic, it’s fantastic.
You can brush my hair, undress me everywhere.
Imagination, life is your creation.
Come on Barbie, let’s go party!

CHORUS

I’m a blond single girl, in a fantasy world,
Dress me up, make it tight, I’m your dolly.
You’re my doll, rock’n’roll, feel the glamour and pain,
Kiss me here, touch me there, hanky panky.
You can touch, you can play, if you say: "I’m always yours"

CHORUS

Come on Barbie, let’s go party!
Come on Barbie, let’s go party!
Come on Barbie, let’s go party!
Come on Barbie, let’s go party!

Make me walk, make me talk, do whatever you please,
I can act like a star, I can beg on my knees.
Come jump in, be my friend, let us do it again,
Hit the town, fool around, let’s go party
You can touch, you can play, if you say: "I’m always yours"
You can touch, you can play, if you say: "I’m always yours"

Come on Barbie, let’s go party!
Come on Barbie, let’s go party!
Come on Barbie, let’s go party!
Come on Barbie, let’s go party!

CHORUS

CHORUS

Come on Barbie, let’s go party!
Come on Barbie, let’s go party!
Come on Barbie, let’s go party!
Come on Barbie, let’s go party!

Oh, I’m having so much fun!
Well Barbie, we are just getting started.
Oh, I love you Ken.

[Oh, I love you Ken!]

July 19th We all depart for the airport and say farewell to Adrian and David. The rest of us kill a day in a hotel at the edge of the airport, with an interesting adventure in the evening involving an endless bus trip (I think the driver must be Kafka) and a meal in a restaurant where no-one speaks any English at all.

July 20th The flight home is grim of course, but we are buoyed up by thoughts of home. There is a greeting party at the airport, and suddenly it is all over for another year.

Thank you to ...

Everyone. To all the young people who came to our camps to put pressure on the team to get better. All the students who sat mathematics competitions in the UK, and their teachers, and the people who invent, administer and mark the competitions. To Brian Wilson and Christine Farmer for great backroom work. To Adam McBride and friends at the BMOS for unswerving encouragement. To Peter Neumann, Angela Gould and all at UKMT, DfES and ARM for funding and much else. Springer for books. Oundle School, Trinity College Cambridge and the University of Bath for donating facilities. Christopher Bradley for sessions and wonderful training materials. Our Hungarian friends especially the deputy leader Sandor Dobos and Cili Kulcsar of the Bolyai Society. Ceri Fiddes for looking after the shadow IMO team back in the UK and much else. The small army of volunteers prepared to lay on coaching sessions in camps all over the country and not otherwise mentioned in this list, including Thomas Barnet-Lamb, Robin Bhattacharyya, Matt Fayers, Mary Teresa Fyfe, Tony Gardiner, Tim Gowers, Ben Green, Imre Leader, Paul Russell, John Silvester and John Slater. David Godwin and James Cook University for warm hospitality. Junko our guide and all the organizers and helpers at Tokyo IMO 2003. All the other leaders and deputies who make IMO such a pleasant experience, especially the Irish leader Donal Hurley and observer James Cruickshank who had to endure merciless teasing about Martin Orr. Adrian Sanders and Richard Atkins for the fantastic job they did on tour. Finally the UK team itself, which did such a great job building on the firm foundations laid down by its predecessors. I also compliment the complement of these people, and assure you that I will never complement these compliments.

Geoff

For more information contact the UK IMO team leader, Dr Geoff Smith, Department of Mathematics, University of Bath, Claverton Down, Bath BA2 7AY. He can also be reached at G.C.Smith@bath.ac.uk

Return to IMO Register home page