UK Leader’s Report, IMO 2004
Geoff Smith
28-vii-2004

The 45th International Mathematical Olympiad was held in July 2004 in Greece. It was a tremendous success. This was the latest cycle of the annual world championship of secondary school mathematics. Each participating nation may send up to six contestants. In common with the sporting Olympic Games, this is a competition between individuals, not nations, though friendly rivalry between states adds spice.

The examinations were held on consecutive days in the University of Athens. There were three questions on each day, and the students had 4 hours 30 minutes to address them. The problems were drawn from the four traditional subject areas: algebra, combinatorics, geometry and number theory. The team leaders arrived in Greece on July 6th and formed themselves into the oracular jury at Delphi. They carefully selected questions at this magnificent location, perched on the side of Mount Parnassus. The air was clean and mercifully cooler than in the Athenian cauldron. From a height of nearly 1000m the view was extraordinary; the unspoiled landscape sacred to Apollo drew the eye down to the Mediterranean Sea.

Two new nations were welcomed into the IMO fold: the Kingdom of Saudi Arabia and Mozambique. Originally 87 nations were scheduled to participate, but unfortunately in the event neither Guatemala nor Tajikistan were able to come, so we had a contest among students from 85 nations. The Arab world is usually not represented well at IMOs, but I am delighted to report that four Arab nations attended the 45th IMO: the Kingdom of Saudi Arabia, Kuwait, Morocco and Tunisia.

The UK team consisted of UNK1 Giles Coope (Fallibroome High School), UNK2 David Fidler (Haberdashers’ Aske’s), UNK3 Paul Jefferys (Berkhamsted Collegiate School), UNK4 Martin Orr (Methodist College, Belfast), UNK5 Alexander Shannon (Kings School, Canterbury) and UNK6 Anne Marie Shepherd (Ilkley Grammar School). The team leader was Dr Geoff Smith of the University of Bath. The deputy leader was Mr Adrian Sanders of Trinity College, Cambridge. The UK Observers were Dr Jeremy King of Tonbridge School and Mrs Patricia King of Benenden School and the Executive Committee of the British Mathematical Olympiad. The three UK reserves were Alexander Davies of Winchester College, Matthew Lee of Robert Smythe School, Leicestershire and Alex Smith of King Edward VI Five Ways, Birmingham. Dr Vin de Silva of Stanford University attended the pre-IMO camp as a coach.

Here are the questions of the 45th IMO. The wording is the one actually used in the English language version. The countries which submitted the problems are indicated.

Day 1

1. (Romania) Let ABC be an acute-angled triangle with 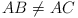. The circle with diameter BC intersects the sides AB and AC at M and N, respectively. Denote by O the midpoint of the side BC. The bisectors of the angles BAC and MON intersect at R. Prove that the circumcircles of the triangles BMR and CNR have a common point lying on the side BC.

2. (Korea) Find all polynomials P(x) with real coefficients which satisfy the equality

   P(a - b) + P(b - c) + P(c - a) = 2P(a + b + c).

   for all real numbers a, b, c such that ab + bc + ca = 0.

3. (Estonia) Define a “hook” to be a figure made up of six unit squares as shown in the diagram

   

   or any of the figures obtained by applying rotations and reflections to this figure.

   Determine all m × n rectangles that can be covered with hooks so that

   • the rectangle is covered without gaps and without overlaps
   • no part of a hook covers area outside the rectangle.

Day 2

4. (Korea) Let 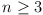be an integer. Let t₁, t₂, ..., t_n be positive real numbers such that

   

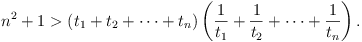
   Show that t_i, t_j, t_k are side lengths of a triangle for all i, j, k with .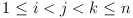

5. (Poland) In a convex quadrilateral ABCD the diagonal BD bisects neither the angle ABC nor the angle CDA. A point P lies inside ABCD and satisfies

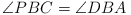   and .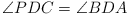

   Prove that ABCD is a cyclic quadrilateral if and only if AP = CP.

6. (Iran) We call a positive integer alternating if every two consecutive digits in its decimal representation are of different parity.

   Find all positive integers n such that n has a multiple which is alternating.

I would be interested to read original solutions to these questions, especially the more demanding problems 3, 5 and 6. Please post them to Dr G C Smith, IMO 2004 Solutions, Department of Mathematical Sciences, University of Bath, Claverton Down, Bath BA2 7AY.

Here are the performances of the UK team. The jury aims to make the questions of increasing order of difficulty on each day, and to make the questions on the second day a little harder than on the first. Each question is marked out of 7 points according to a strict marking scheme. In 2003 the United Kingdom students cleaned up on the relatively easy Problems 1 and 4 with 82/84. This time we were not quite so efficient and secured 78/84.

Here is our table of performance:

       P1   P2   P3   P4   P5   P6    Total  Medal

UNK1    7    2    2    7    3    2      23   Bronze 

UNK2    7    6    1    7    3    0      24   Silver

UNK3    7    7    2    7    3    6      32   Gold

UNK4    6    7    2    7    0    0      22   Bronze

UNK5    2    6    0    7    1    0      16   Bronze

UNK6    7    1    1    7    1    0      17   Bronze

Total  36   29    8   42   11    8     134

Medals were determined as per the regulations. At most one half the participants may receive a medal; happily this year the bound was achieved. The medals are then awarded approximately in the ratio 1:2:3, gold:silver:bronze. Paul Jefferys’s gold medal and David Fidler’s silver medal were obtained with no margin of error whatever, as was Alexander Shannon’s bronze, the cut-offs being 32 gold, 24 silver and 16 bronze. Paul Jefferys is the first UK contestant to have secured 4 IMO medals (B 2001, S 2002, G 2003, G 2004). In 2003 he also scored the gold cut-off mark and in 2002 he was one mark below it. David Fidler improved on his bronze medal of 2003. Martin Orr slipped back from silver in 2003 to bronze in 2004. He hails from Belfast so he becomes the second Irishman to secure two IMO medals, and so far is the only one to obtain a silver. Martin is the only one of our players who will be eligible for IMO 2005 in Mexico. This year Martin was not the all-Ireland champion, since a contestant from the Republic of Ireland secured a bronze medal with one more mark than Martin. That young man will also be eligible for IMO 2005, and it is to be hoped that their friendly rivalry will spur them both on to even better performances next year, and that Martin will come out on top.

The three newcomers to the UK team were Giles Coope, Alexander Shannon and Anne Marie Shepherd. Giles was unlucky not to get a silver medal, falling just one point short. Anne Marie and Alexander were our most inexperienced players, both entering training less than a year ago (Alexander only since April 2004), but they did all that was asked of them, and pocketed their bronze medals.

The UK medal haul 1G, 1S, 4B was only slightly inferior to that of last year (1G, 2S, 3B) and it was heartening that all team members received medals. I am confident that each of our three reserves (Alexander Davies, Matthew Lee and Alex Smith) would have secured a medal had they participated. Our overall national ranking slipped from equal 10th to 20th. Several former Soviet Republics and Far Eastern teams hurtled by us. In my opinion the team of 2004 was about as good as that of 2003, but this time the harder questions on the papers were not quite so hard as in 2003. Our weakness on the tough problems was exposed, though it was very pleasing that Paul solved Problem 6, and David’s partial solution to Problem 5 was a joy.

The IMO is a contest between individuals, not nations, but inevitably the table-makers will have their way, and team performances are compared by their overall mark. This is absurd of course. Some nations are prosperous and can afford to pamper their teams. Other nations are so populous that a sufficiently diligent trawl through their schools is bound to produce a strong team. Yet more nations have education systems which focus whatever resources are available on the intellectually able. There are also countries where the pressure on teenagers to perform academically is more direct than in the more gentle (decadent?) societies of Western Europe. In the United Kingdom we have a fair sized population (60 million or so) and by world standards we are a prosperous country. If we are to engage in friendly national rivalry at the IMO, then our obvious competitors are France and Germany where standards of living, population sizes and attitudes to education are comparable with those prevailing in the United Kingdom. In terms of national performance, we just maintained our position as the leading Western European team, keeping our nose in front of a resurgent German team. Geopolitical changes outside the competence of the IMO jury mean that the UK is no longer the leading nation in the European Union; two new members of the Union swept past us. Our training partners Hungary came a magnificent 1st, and Poland a worthy 2nd. In the Commonwealth the UK ranking slipped from 1st to 3rd; India are the champions this year, with Singapore in 2nd place.

Four students secured perfect scores. They came from Canada, Hungary, and two from Russia. The young man, Béla Racz, from Hungary is an old friend of the UK team from our common training sessions, and it is delightful to see him doing so well. It was also most pleasing to see Jacob Tsimerman from a Commonwealth country, Canada, achieving a perfect score.

Now we once again resort to the annual device which enables the UK leader to burst the shackles of truth. The tenses may vary, but a self-serving version of reality remains the underlying theme.

Leader’s Diary

This diary has become read internationally on the web. It is extremely easy to give accidental offence, especially when trying to portray events in a light-hearted manner. Any negative comments about aspects of the organization must be seen against a background of the overwhelming success of the 45th IMO, and the hard work of many hundreds of people who made it all work so well. Moreover, jibes at other leaders and deputies, co-ordinators, guides and team members should be regarded as the self-indulgent ramblings of a sad man.

July 3: Today I meet five of the team, the deputy leader Adrian and a trainer Vin at Heathrow. Vin has flown in from the States to help. Alexander Shannon is staying behind in the UK because of long-standing musical commitments. He will join the team next week with the two UK observers Jeremy and Patricia. The plane journey to Athens was uneventful, and I am pleased that Olympic Airlines is at last trying to live down its flying ashtray reputation. The new Athens airport is quite a sight for me, since I knew its less swish predecessor very well. The party fits itself into three taxis and we head for the Armonia hotel. At least, that is the plan. The taxis have clearly been upgraded for the Olympic Games. The meters work, and the drivers no longer tell you implausible stories about your hotel having been destroyed by meteorite (but they always knew an excellent alternative which would give you a good deal). I am in the lead taxi, and am troubled by the difficulty I have convincing the cabbie that we want the Armonia hotel rather than Omonia. The Armonia is due south of the airport, away from Athens city centre which, worryingly, contains a district called Omonia. After a while the drachma drops and we call the other cabs by mobile telephone. Happily the third taxi is driving into the sun, but unfortunately Adrian’s vehicle has the sun at its back. We pass the telephones to our respective taxi drivers, and my driver tells Adrian’s driver to hang a .

When we arrive the receptionist at the Armonia assures me that I have only booked beds for six people but expresses concern that there are eight of us. I point out that one can only reserve rooms of one type using their internet reservation system, and that he may find that I have made a second reservation. All is well. We dine in the hotel and go to bed early because we have a flight to the island of Limnos in the middle of the night. We troop to bed passing the poolside disco as it is being set up.

July 4: A few hours later the bleary party walks past the disco again as it is being dismantled. Three cabs take us to the airport where we board a turboprop. We land soon after dawn in Limnos, a quiet island in the Northern Aegean, close to Lesbos and Turkey. It is famed for its refreshing winds. We board the usual taxi convoy and head for the Porto Myrina Palace. This joint is 5 star but out of season. Now 5 star on a Greek island is not the same thing as 5 star in a capital city (where you should be able to see your reflection in the marble floor), but nonetheless it is very agreeable, and I can see that the team members from state schools are impressed. The receptionist reasons, with faultless Greek logic, that the student’s surname ‘Shepherd’ should be pronounced ‘Sheffard’.

We spend the day swimming in the hotel pool and recovering from the journey. We stroll towards Myrina looking for a taverna for lunch, and discover a cheap and pleasant place with a friendly waitress who is a refugee from Cardiff. She steers me clear of the dodgy grilled octopus. Given that I am English, this is a remarkable act of kindness. I have been issuing problem sheets to the team on attractive University of Bath pastel A4 sheets at random moments to add to the gaiety of life, and from time to time Adrian’s cry of “trig drill” means that the students have to face a public grilling concerning some of the more attractive formulas found towards the back of La géométrie du triangle, the masterwork of Lalesco (it is even more thrilling in the original Romanian). I particularly enjoy post-prandial trig drill.

July 5: The team is up early for they have their first practice IMO exam. I have a chance to inspect the island which seems idyllic save for the fancy military equipment bristling on the hilltops. We are precisely in the area where the Greeks and Turks like to wind one another up by flying fighter jets 10 metres inside their own airspace. The heat of the day sets the cicadas off at a terrible rate. I quiz the team as to what is causing the noise, and receive perfectly genuine ignorant suggestions. Thank goodness we are not going to the biology olympiad (electricity lines humming indeed). In the evening we watch Greece beat Portugal 1-0 in the European soccer final on a large outdoor TV near the pool. The Greeks seem happy about this in a curiously Mediterranean sort of way (no vomiting or damage to fixtures).

July 6: I depart very early in the morning to join the jury on the mainland. I leave Vin and Adrian my remaining multicoloured pastel problem sheets, and copies of key works. Following local advice, I ignore STA Travel’s injunction to arrive at the airport 90 minutes early, and turn up with barely an hour to spare. The place is virtually deserted and the check-in is shut. Happily the Everest food outlet is open and I enjoy a double espresso with cheese and spinach pie. I doze all the way to Athens airport, and am met by a Greek young man who is very efficient and does sunglasses very well. I am taken to the international arrivals area where a handful of other leaders have arrived, including those of Spain, Thailand, Saudi Arabia and Macedonia. We board an IMO bus after a short wait and drive to Delphi. It takes about three hours. You first pick your way out of Athens, then across a cotton growing area, and finally up into the mountains. The modern town of Delphi clings to the side of Mount Parnassus. Coaches cannot turn round on its narrow streets, but there are large rotation zones at each end. This makes for some complicated journeys, and I am minded of the theorem that you can turn round a needle of zero width in an arbitrarily small area. We try to drop off some of the leaders at a hotel, including the leader of Kuwait. Unfortunately he isn’t on the bus, but an obviously misidentified leader of the Kingdom of Saudi Arabia is. After a while the driver correctly decides that Kuwait and Saudi are sufficiently similar and lets the KSA leader off. The driver then fails to find my hotel several times. This involves much threading through narrow streets and embarrassing rotations. At last the Macedonian leader and I are dropped at our hotel.

Next I wish to demonstrate how to lose friends by making light of a serious issue. There is a curious language game being played. In Greece it is not done to refer to the country called Macedonia by that name. It is called Fyrom (the Former Yugoslav Republic of Macedonia). Thus every time the relevant leader is asked who she is, she claims to be the leader of Macedonia, and her Greek interlocutor simply nods and says Fyrom. To an outsider it has a surreal air.

I stroll around town, meeting various old and new friends. I meet one leader whom I will not identify but who has clearly not been properly briefed. He has brought US dollars as the medium of exchange, and is under the impression that the native tongue of Greece is English. Don’t ask because I won’t tell.

In the evening we finally get copies of the problems short-list, about 30 questions culled from suggestions sent in by problems committees around the world. I have no idea if any proposals are British, since I don’t look at our six suggestions. This means that I can argue for and against questions with a clear conscience. There is a delightful geometry question which looks a certainty for Question 6 until it is sabotaged by the Japanese leader who gives a precise reference to a very similar question in his problems literature. That beauty was actually the only British proposal to make the short-list, and the squad of 2005 will really enjoy it. The short-list of IMO x is classified until IMO x + 1, so one has some very good questions to tax the students on.

July 7–10: Over the next few days we pick the questions. There is a strong temptation to revert to traditional ways. The sibyl of Delphi is the voice of Apollo. This woman is always called Pythia, and must be an older woman who has led a blameless life. Looking around the jury room, I see that we may be in difficulty (because of the youth of all the female leaders). It would also have been necessary for a goat to be sacrificed and its entrails inspected by priests (presumably the Problem Selection Committee). Mindful of the fact that the UK team contains four vegetarians, and the difficulty of selecting a sibyl (taking the Pythia), I assent to the construction of the IMO papers using more modern methods.

We decide that there are really only three sufficiently straightforward questions to be Problems 1 or 4, so we choose those first. Problem 1 will be a geometry question containing a booby-trap, and Problem 4 is a neat but relatively undemanding inequality. It is cute though. Try it.

We then move to choose Problems 3 and 6. We have lots of choice, and there is a consensus that we should have one on combinatorics and one on number theory. I am not that impressed with the pair selected; the difficulty may be about right, but neither problem is civilized mathematically. Whisper it softly, but they both have the aura of a puzzle.

Finally we select the supposedly medium hard Problems 2 and 5. This time the aesthetics are better; we get a sweet polynomial functional equation and a geometry problem with teeth. The geometry involves demonstrating that one condition holds if and only if another does. One way is merely taxing. The other way will really sort them out.

When the questions have been selected the task is then to get them translated into all relevant languages (about 50). This process begins with the English Language Committee (ELC), which I chair. I invite everyone to join the committee since exclusion so easily causes offence. Now that English is Orwellian worldspeak, it is nonsensical for the native speakers to try to claim exclusive rights. This is the quid pro quo for English being the lingua franca of the mathematical cognoscenti and IMO apparatchiks. I had long since spotted an error of English in the existing draft of Problem 5, and curious to see if it would be picked up, kept silent until the ELC met. It was then appropriate to reveal the howler and suggest a fix. The ELC takes about an hour and a half to come up with its proposals. The jury then reconvenes, and goes through the traditional ritual of criticizing the proposals, debating changes to the wording, and usually deciding that the ELC wording is actually fine. Secretarial assistance in the ELC is kindly supplied by the Leader of Canada, Christopher Small.

Then there is the frenzy associated with typing the English version, and then getting it translated into the other official languages of the IMO: French, German, Russian and Spanish. Next we needed to make versions in all the languages that the students wanted. For almost all languages this was done in LaTeX. For reasons which were never explained, the organizers were planning to automatically convert LaTeX to WORD. This caused chaos. The software tried to improve the spelling of languages it was never designed to meet. The Afrikaans was particularly badly mangled. Even the English version had ‘nor’ changed to ‘not’. The diagram of little squares was changed into a diagram of rectangles. At length it was decided not to use WORD after all (a wise move).

We are having lunch every day at the jury site, but most evenings we enjoy the hospitality of the mayor of a nearby town. This is a splendid arrangement, and gives the opportunity to both individual and massed South American singers to entertain the rest of us. I take the opportunity to have the Cuban anthem Guantanamera translated (loosely) into English. It is a boy-meets-girl poem, drastically shortened for the song. I decide that in future there must be a British response. I will be working all winter on my rendition of that profound exploration of our common fate in the context of missing headgear On Ilkley Moor bar t’at.

July 11: The opening ceremony. This involves two journeys of three hours each to get to and from Athens. On the way one of the buses goes on the blink, but is swiftly fixed by the drivers. We drive past the new Olympic Stadium en route to the hall. Then we have the opening ceremony. Politicians never quite get the IMO (but we are all very grateful because they are bankrolling the whole show). We get to listen to a lot of stuff about football and the Olympic Games which is no doubt supposed to flatter us by putting the IMO in an heroic context. I wager that almost everyone concerned with the IMO regards it as far more important than quadriennial lowbrow jockfests. The best thing about the opening ceremony was a recital on a hydraulis, a recreation of a recently excavated instrument from classical Greece. It is a pipe organ where an assistant has to pump away to keep the air going. Henceforth I shall think of the Scottish piper at the opening ceremony of 2002 as using a portable hydraulis.

July 12: The leaders gather at 9am in the Delphi jury room as the students sit down to the first paper in Athens. For the first half-hour the students are allowed to ask questions about the paper. These are then faxed to Delphi. The relevant leader then suggests a reply to the jury. If this is agreed, the reply is faxed back. This session was very quiet, with only 21 questions. The examination arrangements are never seen by the jury, but as time goes by stories about the invigilation system start to filter back. Invigilators are always on call when a student needs them.

July 13: On the second day of the examination the jury receive a very large number of questions, mostly concerning the meaning of the term parity. In the afternoon the leaders embark on their favourite bus journey to Athens. We are taken to the Marriott, a classy N-star outfit about a 15 minute cab ride from the students’ hotel. Late in the evening the UK students join us at the Marriott for a small celebration. As they chat with us the second days’ scripts arrive. Adrian and I make our excuses and leave to burn midnight oil. Patricia and Jeremy will shepherd them home.

July 14: Co-ordination begins. In the hotel foyer after breakfast I find one of the Problem Selection Committee in melt-down. Apparently large numbers of co-ordinators have not turned up, and a problem captain is still asleep. This is going to be interesting.

Since there are four adults working on the UK scripts, we need space. I go scouting round the hotel and discover that the jury room is not in use. We decamp to this impressive space, a room for over a hundred people, and move the furniture to make a base. We carve up the questions so that we will have a complete expert on any one script. Our observers Jeremy and Patricia are keen to be involved. They are allotted Problem 6. Only Paul has made a serious fist of this question; their job is to understand every word he has written, and have a rational explanation for every rough jotting, smudge and crossing out.

We are to co-ordinate Problems 2, 3 and 4 today, then 5, 6 and 1 tomorrow, in that order. The schedule is such that the co-ordinators have not had time to study the scripts in advance, and this rather slows up the co-ordination phase. The difficult issue with Problem 2 is David Fidler’s script. The co-ordinators believe that it is worth doodly squat, whereas we know that he has an almost complete solution. Admittedly there is a lot of misleading padding, but putting the first page together with the last and ignoring the false trails in between takes you almost home. We have to appeal to the problem captain because the co-ordinators don’t follow our explanation. He sees it straight away, and we pocket David’s well-deserved 6/7. Adrian led on all this, and did a first-rate job.

I lead on Problem 3. We are blessed with very quick-thinking and fluent co-ordinators for this question, and it is easy to sort out who deserves scraps and who doesn’t. There is an interesting cultural clash when we are discussing whether or not some work in rough of Anne Marie deserves a mark. We think that it clearly does, but the co-ordinators have to persuade themselves. After an exhaustive analysis of the script, the co-ordinators are on the edge of conceding the mark. Then one of them drops the bomb: “Is this student a girl?”. This massively inappropriate question (in UK terms) fires off alarm-bells in my head, but of course now might not be the right moment to engage in discussions concerning feminism, anonymous examination procedures and Anglo-Greek cultural differences. I venture the reply ‘yes’ and Anne Marie gets her mark.

I also lead on Problem 4. Now we are really lucky, because we are being co-ordinated by a member of the Problem Selection Committee, and he really knows his stuff. This is a very straightforward co-ordination because all of our students have supplied perfect solutions. The co-ordinator carefully checks every line. He is happy with five of the six scripts, but Martin Orr’s highly analytical solution could not be properly read in the time available. The co-ordinator says that he will read it in the evening (there must have been five or six pages of detailed calculation) but that he expects it to be worth 7/7. We casually walk out, and then I do a very careful rereading of Martin’s script just to be sure. I find two completely inconsequential transcription errors. When I see the co-ordinator later I ask him how many glitches he found; he says two. Martin and indeed everyone else gets their 7/7s.

July 15: Adrian leads on Problem 5, a tough geometry question. This is an extremely laborious co-ordination. We are not asking for more than 3/7 for any of our students. The default method is an arduous and complex angle chase. The co-ordinators correctly insist on checking every line, but it does take a very long time. Then we find that we have a difference of opinion concerning David Fidler’s script. The co-ordinators do not believe that he has given a proof at all, whereas we believe that he has given the best proof of any of our students. It is worth explaining what David has done. He took the geometrical configuration in question, and drew some extra lines. The effect of the extra lines is to make a figure which has an axis of symmetry (the original configuration was not symmetrical). The existence of this symmetry enables one to read off the required result. This was geometry in the spirit of Felix Klein and Henri Poincaré. I thought we would all stand up and hug for the joy of it all, but the co-ordinators take another view. This is not proper geometry they say. No triangles are mentioned. No angles are calculated. One of them says ‘I am here to defend Euclid’. We appeal to the problem captain who, fortunately, is more sympathetic to methods popularized after 330 BC, and David gets his 3/7.

Finally we have a problem with Paul’s script. We are asking for 3/7. His argument is long and trigonometric. The co-ordinators are clearly unimpressed by Paul’s admittedly convoluted wizardry (even though he does use triangles). Eventually they accept that the main thrust of Paul’s argument is correct, but argue that he has not dealt accurately with degenerate cases. Adrian argues that he has, and after involving the problem captain again, Paul finally gets his 3/7.

The co-ordination of Problem 6 is led by our observer, Jeremy King. Only Paul had a serious attempt at a solution. Initially the co-ordinators seem sceptical, but as they work through all the details and side cases, I can see that they are becoming progressively more impressed with Paul’s analysis. Jeremy’s complete mastery of the argument is a great help of course. Paul has overlooked one case. His work is clearly nearly a full solution, but he must lose at least one mark for his oversight. The omission is easy to fix by using a method which Paul had already invented, and by now the co-ordinators are sympathetic to his solution. We have two pieces of intelligent work in rough which Jeremy hopes will convince the co-ordinators that Paul should only lose 1 mark. He only has to show them the first piece of evidence, and they award 6/7.

Finally we move to the co-ordination of Problem 1 led by me. This proves a fraught and difficult co-ordination. We are first kept waiting for two and a half hours because Australia pinch our slot (thanks Angelo). Many of the co-ordinators for this question knock off early and go home because they do not live in Athens. We have a single co-ordinator, who is clearly over-worked. We are asking for 7/7 for Giles, David and Paul, but we know of minor flaws in the other three scripts, so are expecting 5/7 or 6/7 for each of those. He immediately offers 7/7 for Giles and 6/7 for Martin, which we accept (I had been worried that Martin might only get 5/7 which would have extinguished all hope that he might just scrape a silver medal). After careful reading, he gives us 7/7 for David and Paul. He explains that there is a problem with Alexander Shannon’s script, so we move on to Anne Marie’s paper. We are asking for 6/7. He says that although it isn’t perfect, she may have done just enough to get 7/7 because of her (incomplete) analysis of degenerate cases. We sit bemused while he convinces himself that her script was worth 7/7 according to precedent set throughout the previous two days. Here we were getting the benefit of going last; some hard-nosed leaders have clearly been arguing that black is white, and the co-ordinators have given ground somewhere on the way. In order to be consistent it must be the case that black is white for us too. Lucky Anne Marie I say.

Next comes Alexander Shannon’s script. His solution has two imperfections. The first is a hole, and the second is that his punchline is too slick. We had not really noticed this second fault, and still think the criticism was unduly harsh (he did not explicitly spell out an obvious step). The hole takes the following form. Alexander wants to show that four points are concyclic. His method is indirect, cunning and ridiculous. He reduces the problem to verifying a trigonometric identity. He makes a transcription error in writing down the expression which forms one side of the target equation but it does not matter because he makes no attempt to demonstrate this trigonometric truth. As soon as we had received Alexander’s script, Adrian and I raced to fill the gap. We quickly found the necessary trigonometric argument; it takes three lines, but contains a cute algebraic trick. This is a shame because it indicates that filling the hole is not a triviality. We have the trigonometric argument written out for the co-ordinator. The co-ordinator is dismissive of our trigonometric patch, but not for the correct reason. He points out that we have used cotangents (which he apparently regards as obscure). This is absurd. Our point is not that Alexander could have found this argument, but merely that in principle his method was correct and could be made to work. We hoped for 5/7 but feared 4/7. We are astonished to be offered 2/7. The breezy way in which Alex had closed the argument is really counting against him. It is the end of an exhausting co-ordination, but Alexander is going to get a bronze medal (we hope).

As usual Gordon Lessells, the Irish Deputy, is the man with the numbers. and he correctly predicts the cut-offs and we breathe more easily as all our students have got medals, three of them with no margin of error. The jury meeting confirms the cut-offs. The UK medal haul is almost as good as last year, but our position in the unofficial national rankings has slipped to 20th. Three fewer marks in the wrong places and our performance would have looked rather sour (a silver and four bronzes). We were very lucky this time.

July 16: The enthusiasts went on an excursion today, but Adrian and I were exhausted and spent the day sleeping. In the evening we went over to the students’ hotel and joined a party which went for a meal in a taverna beneath the Acropolis. This involved tangling with the Athens metro. This has undergone the same gentrification as the airport. The Swiss team were kind enough to show us the way, and we had a fine time. Our student Giles is in a very good mood having done so well, and seems keen to improve Britano-Helvetian relations. He threatens to lead an insurrection when Adrian and I call time. He is a fine fellow and quickly falls back into line.

July 17: Today we had a fine closing ceremony. By now the European Football is starting to fade, and the forthcoming sporting Olympic Games are starting to dominate the politicians’ thoughts. In the evening we have a magnificent alfresco banquet at a golf club by the sea. We are entertained by Greek dancers. Inspired by this, hundreds of students take part in Greek dancing, and the Dutch leader seems to lose about 30 years. Rumours circulate that the Advisory Board Chairman is about to take the stage, but in fact he comes over to see me to discuss future training arrangements. He has a constructive suggestion as to how to improve morale.

July 18: We spent the day at Athens airport, because Olympic Airlines rescheduled our flight. This is annoying but is not enough to allow Olympic to join my all time list of truly awful airlines (Austrian Airlines, British Airways and Malev). By the end of the day, Olympic will have made it though. Our student from Belfast, Martin Orr, is going to miss his connecting flight. The helpful Olympic Airlines receptionist at Athens airport assured me after tapping at her screen that (a) there was plenty of availability on Heathrow–Belfast flights that evening and (b) Olympic Airlines in London would arrange for a ticket for Martin on one of those flights. When we arrived back in London, both of these statements proved false, and Martin was stuck in London for the night. So well done Olympic Airlines, you have made the list. Detailed explanations of the crimes of the other tatty outfits is available on application. Don’t use them if you can avoid it.

Acknowledgements

I would like to thank the Greek organizers of IMO 2004 for putting on such a splendid event. I must also express warm thanks to the UK IMO team and reserves for making my job an unalloyed pleasure. Leaders, Deputies and Observers of the countries which participated in IMO 2004 made the experience a joy. I would like especially to thank the Leadership of France, Ireland and Luxembourg for showing me how to use the Euro. I have retained various denominations as I expect my grandchildren to be curious about what will (by then) presumably be an extinct currency.

The UK IMO effort is the work of so many people that it is not possible to name them all. There are all the students who participate in the various mathematics challenges and olympiad competitions, and their teachers. There is the United Kingdom Mathematics Trust, its Council, its Executive Director Angela Gould and the staff of the Leeds Office. There is the British Mathematical Olympiad Subtrust under the redoubtable chairmanship of Adam McBride. There are the markers for all the competitions. There is now a very large national mentoring scheme to help bring on strong students of various ages under the direction of the previous Deputy Leader, Richard Atkins. There are the students of the UK squad who have made the various training camps such fun, and the small army of trainers who have helped at camps, including Jeremy King, Patricia King and Vin de Silva in Greece.

Our continuing co-operation with the Hungarian squad is of considerable benefit to both countries, and I thank Sandor Dobos and Cecilia Kulcsar for making all this possible. Mircea Becheanu of Romania was our guest trainer at Trinity College, Cambridge this Easter, and we thank him for his help.

I must single out Christopher Bradley for his geometry coaching. I have to keep a wary eye on my deputy Adrian Sanders who does his job and mine much of the time. The ex-olympians have helped in diverse ways, including Joseph Myers’s web expertise. As I write this, UKMT’s founding Chair of Council has finally been allowed a graceful retirement. I am sure that we all wish Peter Neumann a complete restoration of his good health. His successor Bernard Silverman FRS (an IMO Gold Medallist) has a hard act to follow.

Finally it is appropriate to thank our sponsors: the Department for Education and Skills, the United Kingdom Mathematics Trust, Trinity College Cambridge, the microelectronics company ARM and the publishing house Springer.

Return to IMO Register home page