f ( f (x) + y ) = f ( f (x) − y ) + 4 f (x) y for any real numbers x, y.
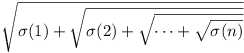is a rational number.Note: A permutation of the set {1,2,...,n} is a one-to-one function of this set to itself
Many countries encourage and test their brightest students with national competitions in mathematics; at a higher level there are regional competitions in which national teams compete, such as in Latin America and the Asia Pacific region, and most significantly there is the prestigious annual International Mathematical Olympiad (IMO) which is attended by teams from about ninety nations.
Greek, Romanian and Bulgarian mathematicians met in Paris in the early 1980s and decided to start a mathematical tournament for south-east Europe. In 1984 the first Balkan Mathematical Olympiad took place in Greece. The competition has expanded over the years, and this year we had 14 teams : those from the 9 Balkan member countries, and also from 5 guest countries, which were the UK (competing for the third time), Kazakhstan, and the newcomers Italy, Azerbaijan and Montenegro. There is a rota of countries to host the event - 2007 was Greece’s turn; they chose to organise the Olympiad in Rhodes, so for a second consecutive year a Mediterranean island played host (in 2006 it was Cyprus).
Over half a million people each year take the Mathematical Challenges (JMC, IMC and SMC) in UK schools, and strong performers proceed to subsequent papers. At the senior level we have the two rounds of the British Mathematical Olympiad, the results of which are used to select twenty students for a training camp in Cambridge in March / April. These twenty take two further examinations in Cambridge, after which a squad of eight or nine is chosen, from which the team for the IMO is selected at a later date. At the same time as the IMO squad was picked this year, a team of six was chosen for the Balkan Olympiad, a team which deliberately contained inexperienced students, none of whom had been to an Olympiad before - in fact none was in their final year at school. Four of the nine were also in the IMO squad. It is worth pointing out that most of the countries send their strongest possible teams to the Balkan Olympiad; for example Serbia sent exactly the same six that will go to Vietnam for the IMO later this year.
The UK team chosen was :
| Ian Fraser | (16) | Torquay Boys’ Grammar School |
| Tom Lovering | (17) | Bristol Grammar School |
| Freddie Manners | (17) | Winchester College |
| Preeyan Parmar | (16) | Eton College |
| Dominic Yeo | (17) | St Paul’s School, London |
| Alison Zhu | (17) | Simon Langton Girls GS, Canterbury |
The two leaders of the UK contingent were school teachers Robin Bhattacharyya (Highgate School, London) as leader and Vesna Kadelburg (Sevenoaks School, Kent) as deputy leader.
Thankfully, everyone selected found that they would definitely be able to attend, with Freddie managing to rearrange his German oral examination. The team prepared in the short three week period between selection and departure by practising with past questions. Rhodes is a very popular tourist destination for people from the UK, but flying there direct is only possible on Wednesdays and Saturdays; so we had to fly with Olympic Airlines via Athens.
The team was to gather at Heathrow by 10.15am on Thursday. I arrived at 10am and was relieved to see that all six team members were already there, and in good spirits. Ian had the longest journey, rising at a quarter to five in Torquay, and getting a lift from his dad, who also picked up Tom in Bristol on the way. Everyone had their passport, but we had a short wait for deputy leader Vesna to arrive with some of the plane tickets, and our new navy blue team T-shirts, as trains from Kent had been diverted because London Bridge station was closed. It wouldn’t be the last time during the week that we would be waiting around because of late transport !
On the plane to Athens, Ian showed me a nice solution of his to a tricky Balkan Olympiad question from a few years ago, while Tom read a book on number theory; Freddie tried past competition questions on his own, and others played cards or listened to music. We were scheduled to have just an hour and a quarter transferring at Athens; we rushed through, were directed to leave the airport, passing through customs, and then come all the way back, through security. We made it on time, and Dominic noticed that we had come back to the same gate. Four of us were on Row 13 again, and realised from detail on seat covers and the screen used for safety announcements that we were in fact back on the same plane and in fact in the same seats as we had been for the first flight !
This was in any case all much easier than the last time I came to Greece. Then I’d driven a campervan down through France and Italy with some friends to go to the Olympic Games in Athens. I’d briefly been to Rhodes once before, in the late 1980s, when I arrived on a cruise ship after a couple of days sailing from Piraeus (Athens). We weren’t going to get such a good feeling of distance travelled this time.
Views of the area near Athens from the plane were of rocky hills, whitewashed buildings, and greenery of a different shade from the UK, in a drier environment. During the short flight to Rhodes sunset turned to darkness, so we were unable to get an impression of the island from the sky. We were met at the airport by the Chairman of the Olympiad’s Organizing Committee, Nikolaos Alexandris, who told us that he had lived in Manchester for three years in the 1970s while studying for his PhD; we were taken in three taxis to the Apollo Beach hotel in Faliraki, the well known resort a few miles south of Rhodes Town which is itself at the northern tip of the island. One of our Greek guides who had spent a year studying for a Masters degree in Manchester said that Faliraki reminded her of Blackpool, and even though we were arriving out of season, the neon signs, Kelly’s Irish Pub, bars advertising Premiership football, and a UK tattooing / body piercing place did display the main influences on this particular part of Greece. The hotel was very comfortable, set away from the main road down an elegant driveway, and it had its own swimming pool, and was very close to the beach. The lobby was large, and an excellent place to meet other teams.
There was some confusion about whether Dominic was a boy or a girl (at least on the hotel lists of rooms !) so arranging who shared with whom took some time. Ian, Tom and Freddie would share with each other, Dominic would be on his own, Alison would be with the Italian girl Maria, and Preeyan would share with two Italian boys. The Italian team were around at the time in the hotel lobby and seemed very friendly. Our team went for a brief walk, and then went to bed at about 10pm.
Vesna and I waited in the lobby for a while. Vesna is actually no stranger to the Balkan Olympiad, having competed herself in the 1990s as a contestant for Serbia. Now the team leaders stay separately from the deputies and teams in the early stages of Olympiads, because the leaders have to work through the problems that are short-listed for the competition, and choose which to include for the competition (in the Balkan Olympiad four questions are chosen for a single four and a half hour long exam). To prevent any suggestion of news of the questions reaching the students before the examination, the leaders were to stay in a different part of the island, and everyone had their mobile phones confiscated, until after the exam on Saturday. I was to travel to the secret location with the Albanian and Azerbaijani leaders who were arriving on a later flight, while Vesna would stay with our team.
It was a forty-five minute journey to Kiotari in the south of the island. I had met Edmond from Albania two years before at the Balkan Olympiad in Romania. Fuad from Azerbaijan explained that his team had that day flown from Baku to Istanbul, where they had had to wait for seven hours before flying on to Athens, and then to Rhodes. He was even more tired than I was when we arrived after midnight in Kiotari, and were met by the night porter who eventually found our names on the list of rooms.
The Balkan Mathematical Olympiad comes into and out of existence each year; it is not run by a permanent body, but by each year’s jury. The jury is chaired by someone from the host country, in this case Greece’s IMO leader Theodore Bolis who has been involved in organising several Balkan Olympiads before, as well as the IMO in Athens in 2004. The other members of the jury are the leaders of each team. On the Friday morning Fuad and I tracked down the jury meeting in the ‘Wavelength Room’ which was a function room in another building of the big hotel complex where we were staying; cocktails were advertised on the wall, but this was serious business !
The twenty problems on the short-list were studied. Solutions are provided, but it helps to have a go first. Unfortunately this wasn’t possible for me the previous night as I had arrived too late to receive the problems then. The problems are submitted by participating countries, and some were in fact written by jury members (team leaders), although we were not told which country had written which question until after all the contest problems had been picked.
There are four main areas of Olympiad mathematics : geometry, number theory, algebra and combinatorics. The type of problem posed is very different from those encountered in school mathematics in the UK, hence the need for training camps during the year for students, and a mentoring scheme by correspondence. The jury attempts to pick one question from each of the four areas for the competition paper.
The most important people on the jury are the nine leaders of the member countries of the Balkan Mathematical Olympiad : Albania, Bulgaria, Cyprus, Greece, Macedonia, Moldova, Romania, Serbia and Turkey. Only they can vote on any motion, such as a change of regulations or a decision on which questions to choose for the exam. However, other people present can voice their opinions, including leaders of the guest countries, and the observers that the Balkan maths ‘superpowers’ Bulgaria and Romania brought along to accompany their leaders.
Discussion is only in English, the official language of the competition; leaders who speak good English are more likely to say a lot than leaders who do not. There are very experienced and knowledgeable people on the jury, including Nikolai Nikolov of Bulgaria whose achievements in IMOs in the 1990s put him among the most successful competitors of all time; he actually met Vesna at a Balkan Mathematical Olympiad when they were both competitors. He had plenty to say in the jury meetings, as did the Romanian leader Dan Schwarz who had competed for Romania many years ago in the IMO; Dan later lived in Canada for over twenty years, before returning to Romania.
The nine with a vote each rated the short-listed problems as ‘easy’, ‘medium’ or ‘hard’. The aim is to pick an easy question, two medium questions and a hard question for the exam. When we had a rating (as a mark out of 27) for each question we could think about selecting the questions, starting with the easy one.
There were very few easy questions, and it didn’t take long to pick one of the geometry problems. Then we considered the hard problems. An algebra question was proposed but not seconded, then a number theory problem was proposed and seconded but couldn’t go on to gather the required five votes. Finally a combinatorics question was looked at; it did get the votes, but some weren’t sure that it was hard enough.
The first medium level problem we took was in algebra, which left us needing a number theory question, of which only one was medium. I liked the number theory problem in question, but others did not; the Bulgarians suggested that the algebra question already selected be reclassified as number theory (it had some number theory in it) to give us more options – now another algebra question could be taken. This was accepted, and the final problem was a functional equation (an algebra problem).
We had our four questions, but had to find the best order in which to place them on the exam paper - the idea is to have increasing difficulty through the paper. After much discussion and voting we ended up with the questions in the same order as would be given by the provisional rating out of 27.
We were by no means finished now ! The wording of the questions was discussed in minute detail, and the expression of question four (combinatorics) was changed considerably, in an attempt to avoid misunderstandings about what a polygon is (is a triangle the set of points around the edge, or should we include the interior as well, and does our decision vary from country to country ?). Eventually we arrived at the following :
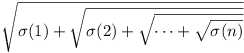is a rational number.We thought that we had found elegant and interesting questions that would test the students. Question 1 seemed quite straightforward, but each of the other three would take some solving. The countries that proposed the problems were Albania (Question 1), Bulgaria (Question 2), Serbia (Question 3) and Turkey (Question 4).
I was the only native English speaker in the jury room, but my knowledge of the language had not been needed – the other leaders were certainly very capable of composing questions in excellent English. Now they had to translate the exam into their own languages, while I had nothing to do but observe.
One of the most fascinating aspects of the competition for me was the use of language. On one occasion I sat on a table with the Azerbaijani, Kazakh and Turkish leaders. The Azerbaijani talked to the Turk in Azerbaijani (very similar to Turkish), to the Kazakh in Russian, and to me in English. He told me that people under sixteen today in Azerbaijan are more likely to speak English than Russian. Serbians, Macedonians and Bulgarians could understand each other; Moldovans and Romanians speak essentially the same language. English, and to a much lesser extent Russian, were the communal languages.
Each competitor would be given the exam in English as well as their national language; Moldovan students would be given English, Romanian and Russian versions. The translation involved pen and paper, dictionaries, lap tops and much discussion. Small groups would crowd around a computer screen as people considered exactly how to translate ‘permutation’ or ‘one-to-one’. Most translations, and most of the jury’s collective work, had been completed by the time we left for the opening ceremony in the north of the island.
The students had been scheduled for an early start on Friday from their hotel in Faliraki, for an excursion to Rhodes Town to see the medieval buildings of the Knights of St John, who had run the island for two centuries. There were some delays with buses, but that gave them a chance to get to know the sociable Serbian team, and to notice that the sign that they had been given to parade with actually said ‘United Kindogm’ and that the sticky letters could be rearranged on the board. Over the next few days many anagrams appeared from Ian and the rest of the team, including ‘Untied Kingdom’, ‘Dog Unit Winked’, ‘Odd Minute King’, ‘UNK Gnome Did It’ (UNK was our official country code for the competition) and finally ‘King Dom United’. The tour guide in Rhodes Town made some memorable comments about the history of the island, and then there was a visit to the mayor’s office, and a press conference. In the afternoon, back at the hotel, the team decided to spend a couple of hours doing a practice exam under some shade by the swimming pool; they found that they’d made good progress, giving them a confidence boost before the real exam. After this they set off for the official opening ceremony of the Olympiad, in Rhodes Town, where they would of course be sitting separately from the leaders who had now decided the contest questions.
The leaders were driven up from the south to the north of the island, a journey taking an hour, to attend the opening ceremony of the Olympiad in the very fancy Rodos Palace hotel, which had its own carpet shop, boutique, hair salon and jewellery shop ! Unfortunately the ceremony began about forty-five minutes late, and the leaders were only able to stay for the first hour of the ceremony, listening to many dignitaries speak encouragingly about the value of participating in the event, about the ancient Greek mathematicians, and about the Dodecanese islands and traditional Greek hospitality. Just as the musical entertainment began, the leaders had to get back on to the bus for the hour long journey back to the south of the island to make it to their hotel in time for dinner ! The students stayed, and listened to some impressive flute playing, and a band from a school of music in Rhodes, and watched the performance of the traditionally dressed Greek folk dancers that the leaders had seen waiting in the hotel as they left. Back at the leaders’ hotel in Kiotari, there were further discussions about the translations after dinner; the translations were all approved and proceedings were over for the evening.
The four and a half hour long exam was on Saturday morning at a
school called Rhodes College, about ten minutes’ drive from the
students’ hotel, but nearly an hour away from the jury
hotel. The leaders were needed at the venue, so that any questions
about the wording of the problems that students might ask (such
queries are allowed in the first half hour) could be answered. There
were several questions, including three from UK team members, all
about question 4. The jury had to approve written responses from the
leaders before they could be taken back to the students.
The UK squad trains with the Hungarians over the Christmas holidays
every year; the official T-shirt of that camp this year was a very
loud shade of yellow. One of our students told me that his parents
found the T-shirt so offensive in colour that they would not let him
wear it in the house ! Mindful of this, Tom and Dominic decided
to wear these shirts to the exam, in the hope of dazzling the
opposition. Unfortunately Tom found that this was unsuccessful, as he
was sat at the back of his exam room !
After some time, the leaders were taken to the students’ hotel in Faliraki, where they would stay for the remainder of the Olympiad so that everyone would be together (well, almost together – the different teams were split between two nearby hotels). Meanwhile, some of the deputies left the exam site to see the aquarium in Rhodes Town, including Vesna and the Serbian deputy Milivoje. They returned to the competition site to pick up the students at the end of the exam, and Vesna set to work grilling our team about exactly which parts of which questions they believed that they had solved. This information is extremely useful when the scripts are marked by leader and deputy.
I chatted at the hotel with the Romanians Dan Schwarz and Radu Gologan, and Magda, the mother of the fourteen year old Serbian student Teodor Von Burg. Dan and Radu had been in Iaşi in Romania for the 2005 Olympiad, where Radu was the main organizer, and Dan led the co-ordination (marking) of the combinatorics question; I had been the UK leader that year, so had met them both. Backgammon was now the game of choice for Dan and Magda.
When the students returned to the hotel I found that they were all confident about Question 1, but there wasn’t much to report about the other problems. Question 2 looked pretty bad; it was harder than it looked, and some students had spent quite some time on it without success. Dominic made encouraging comments about Question 3 – he wasn’t completely confident, but the key steps of his method were identical to those of the official solution; four of our students thought that they might have solved Question 4, but it was the type of question where it was easy to make a mistake or not to explain things fully.
The students spent the afternoon on the beach, skimming stones, and sunbathing. They went for a walk, exploring Faliraki, and the nearby area.
At 5pm (or maybe 5.40pm) there was a jury meeting to discuss mark schemes for the problems, each of which is worth 10 marks. The problem selection committee chaired by Anargyros Fellouris presented their suggested mark schemes, and the jury voted on minor changes. The meeting took an hour, but ended hurriedly with slight confusion over an issue of marks for a construction of an example in part of Question 4. Anargyros had spent three years in Liverpool in the 1980s studying for his PhD, and he had many fond memories of England.
A few minutes after the end of the jury meeting, Vesna and I received the scripts of our students. These had been photocopied, with the copies going to the Greek markers - the way things work is that we come up with an idea of the correct mark, as do the Greek markers, and then there are discussions to determine an agreed final figure. Saturday night was to be our time for marking, and all day Sunday would be for the discussions (the co-ordination), with different teams having different slots for different questions.
So far leader and deputy had been separate for most of the time, as the leader worked on setting the problems, while the deputy accompanied the UK team. Now we had much work to do together. We started with question 1, which was geometry. There was a lot of material to go through, with our team’s solutions in neat varying from one side in length to seven sides. There was less rough work to go through than sometimes, due to the restricted amount of rough paper provided in the exam. Every line had to be checked; it is very easy to make a slip or miss a case. Vesna, who is expert in geometry, drew diagrams for each of the student’s work and we convinced ourselves that the arguments were correct. There were a few typos, and Alison’s approach without trigonometry made checking all the possible cases more difficult, but it was very good to discover that the team had indeed all essentially solved the first question.
The geometry had taken us from 7pm until 11pm. Next we took on the hardest question to mark : Question 4. The official solution was long and difficult to follow; the Serbian leader Milos had found what seemed to be an easier solution, and indeed other solutions existed. It is important in mathematical competitions to justify every step rigorously, and avoid using pattern spotting, or inferences from a diagram that only shows one possible arrangement, to justify your argument. It was obvious to the jury that this would be a difficult question to mark; but it was a nice problem, so it was selected nevertheless.
Ian had the wrong final answer; he had made an unjustified claim somewhere, which was incorrect, and we couldn’t see where it had come from. Dominic had assumed something early on in his argument that was unfortunately false; everything else followed correctly after this, but was mostly worthless, as a flawed mathematical proof is no proof at all. Freddie wrote a terrible line of nonsense near the end of his proof, but otherwise his work was in fact fine, and the hole could be patched up easily. Alison’s work was confusing. There wasn’t much written, so it didn’t look like a correct proof; however it was very difficult to point to anything that was actually wrong with it. Eventually we realised that with the statements and proofs of four easy lemmas (results) added it would be a correct proof. As it stood there were large gaps, and we didn’t know what the co-ordinators would make of it.
Dominic had explained his error in Question 3; we saw that it could easily be corrected so we were satisfied that he would get a high mark. Other people got bits and pieces of results on Questions 3 and 2. In the end Vesna and I finished the marking at 5am !! It is important to read the scripts very carefully, and see what needs to be done to patch up the proofs; we spent a lot of time doing this but our work was not wasted in co-ordination on the following day. My thanks to Vesna for her vital help in this lengthy marking session !
On Sunday the students, having finished their mathematical work for the trip, went on an excursion with the other teams to other parts of the island. Vesna and I were taken by bus back to Rhodes College, for the co-ordination. We had Questions 3 and 4 in the morning. Question 3 went very smoothly and quickly, with the co-ordinators quickly agreeing with us about the merits of the students’ work. Dominic got 9 (out of 10). Half an hour was set aside for each question for each team, but it took us about an hour and twenty minutes to go through question 4. I remember the wry amusement in the voice of the main co-ordinator Dimitrios Kodokostas as we reached the final script, Alison’s, and explained that this was the difficult one : ‘So the others were easy ?’ he asked. He also enjoyed looking at Alison’s ‘purple’ and ‘green’ lines on his (non-colour) photocopy !
We explained in detail what had to be done to turn our students’ arguments into correct proofs. Freddie got 7 marks, which was pleasing; Alison only managed 3, though Dimitrios said that with a little more explanation and proof it would have been 7 or 8. We missed the bus because we took so long, so were driven back to the hotel by the co-ordinators. Finally there was some free time, as the other two questions were to be discussed in the early evening. Vesna and I and our Serbian counterparts Milivoje and Milos headed for the beach, which was deserted as we were out of season. We went swimming, though the water was quite cold, and it took some courage at first ! The water was marvellously clear, and it was certainly worth the effort.
Back at Rhodes College, Question 2 went very quickly, and we got slightly more than we expected, as the co-ordinators were interpreting the mark scheme in a particular way. We were the last team to address the geometry question (Question 1). The co-ordinators went through each solution line by line, and they were eventually satisfied about our students’ proofs; after much thought they had decided to disregard a minor technical shortcoming in Alison’s work because of the beauty of her solution, and in the end we managed a perfect team score of 60 on Question 1. Our co-ordination was now over. In fact the average individual score (out of 10) for Question 1 turned out to be 9.04, with the other questions proving to be much harder, with average scores of 3.91 (Question 2), 3.46 (Question 3) and 2.47 (Question 4).
Our scores were as follows :
| Q1 | Q2 | Q3 | Q4 | Total | |
|---|---|---|---|---|---|
| Dominic Yeo | 10 | 3 | 9 | 3 | 25 |
| Freddie Manners | 10 | 3 | 0 | 7 | 20 |
| Tom Lovering | 10 | 2 | 5 | 0 | 17 |
| Preeyan Parmar | 10 | 5 | 1 | 0 | 16 |
| Alison Zhu | 10 | 2 | 0 | 3 | 15 |
| Ian Fraser | 10 | 2 | 1 | 1 | 14 |
The team total of 107 marks (out of a possible 240) was pleasing.
After the final co-ordination sessions for other teams, including Italy on Question 4 who had missed their slot before lunch because we were spending so long on that question, we had the final jury meeting. Any co-ordination issues that are unresolved are brought before the jury, and there were two cases of an extra mark being sought, and granted. It was agreed that in future guest countries would be invited to send in questions to be put on the short-list for the tournament, as well as the member countries. After a last minute phone call back home, the Macedonian leader dramatically announced that his country had agreed to host the 2008 Balkan Mathematical Olympiad, probably on Lake Ohrid. There was no volunteer for 2009, but the rota suggests that Moldova is likely. The medal boundaries were decided on the basis of a ratio of 1:2:3 of gold medals to silver medals to bronze medals, with two thirds of the students to get medals. The calculations are for member country students; guest countries’ scores are slotted in after the medal boundaries are decided.
The medal boundaries were in fact 33 for gold, 23 for silver and 15 for bronze. So Dominic won the UK’s first silver medal in its three appearances at the Balkan Olympiad, while Freddie, Tom, Preeyan and Alison all won bronzes. Ian was unlucky to miss out by just one mark. The team scores were as follows :
| 1 | Bulgaria | 184 |
| 2 | Romania | 169 |
| 3 | Moldova | 142 |
| 4 | Serbia | 132 |
| 5 | Turkey | 127 |
| 6 | Italy | 110 |
| 7 | UK | 107 |
| 8 | Kazakhstan | 99 |
| 9 | Greece | 91 |
| 10 | Albania | 73 |
| 10 | Macedonia (FYROM) | 73 |
| 12 | Cyprus | 68 |
| 13 | Azerbaijan (3 in team) | 48 |
| 14 | Montenegro (1 in team) | 12 |
Two students had managed to score a perfect 40 : Iurie Boreico of Moldova and Lucian Turea of Romania. Iurie already has three gold medals from the IMO and a silver, and seems very likely to break the IMO record this summer by being the first person ever to win four golds and one silver (and the silver back in 2003 missed being a gold by just one mark !). He may also equal the record of Ciprian Manolescu of Romania in getting full marks at the IMO three times.
Of the sixteen people to beat Dominic’s score, ten have IMO experience, six having been to more than one IMO. Our team is inexperienced, and competed very well; Vesna and I were very pleased with their performance, as were the team themselves.
The team had been on an excursion that day to the ancient ruins of the city state at Kameiros, which was, they tell me, an excellent trip; the ruins were not spoilt by tourism, and the guide who talked about them was very good, and spoke excellent English, refreshingly in an English rather than American accent. The teams were free to wander around on their own, and several of them gathered in an ancient hole in the ground for a photo. Unfortunately it was a windy day, and not suitable for the scheduled boat trip to the nearby island of Chalki. In fact, after lunch at a local taverna, the students were back early, in time to meet Vesna and I on the beach before we went off for the co-ordination of the final two problems in the early evening.
Vesna kept the students up to date with their marks by text message. It was a nervous wait for them, as they tried to take their mind off the scores by attempting Fauré’s Requiem accompanied by Tom on the ukulele. They also played Hungarian snap, some kind of mathematical card game involving a plastic bottle. We didn’t see our students later that day, as after the jury meeting finished at 10pm we were taken off to dinner at a restaurant, where a huge number of starters tested our appetites. The Macedonian leader proposed all sleeping on the beach afterwards, but this was not popular, so we went back to our respective hotels at about 1.30am (some teams stayed at the Apollo Beach, and others at the Esperides).
After four exhausting days of travel, problem selection, marking and co-ordination, the leaders and deputies looked forward to a couple of more relaxed days before departure. Monday brought the main excursion of the Olympiad, with leaders, deputies and teams all together. The first stop was at Petaloudhes, the ‘Butterfly Valley’. In fact the creatures are Jersey tiger moths, not butterflies, and they only appear in July and August, attracted by the oriental sweetgum trees. So there were no butterflies (or moths) to see, but it was a nice walk through a green part of Rhodes, cooler than most of the island, and with a nice stream and waterfall.
From here we went to Lindos, the highlight of the week for me as far as sights went. The village is of whitewashed buildings, and narrow streets, by a beach and a rocky harbour, with the sea truly beautiful shades of green and blue. At the top of a hill stands the acropolis, an area used as a strong point in times of danger for thousands of years. The views of the ancient ruins of the acropolis, and down from there to the sea and village, are spectacular. It was to the village for lunch, outside in the sun, before we sought shade in a café before taking the bus back to Faliraki. We crossed many bridges over empty river beds of seasonal watercourses; rain has been down for the last two years in Rhodes, so we wondered how long ago it was that these rivers flowed. At the hotel Dominic, Tom, Ian and Alison joined in with the Serbs on the tennis courts, though it seems that they were outplayed.
In the evening we were all taken to a bar in Rhodes Town for a couple of hours. The loud Greek techno music didn’t help conversation or encourage many to dance, but the Macedonian leader and deputy were certainly on the dance floor, as were some of the Greek organisers and guides, with the Cypriot leader. On the bus back to the hotel the Serbians and Macedonians began singing loudly (songs from the 1990s according to Vesna) so Dominic, Tom and Ian who all sing in choirs, launched into a hearty version of Jerusalem, followed by I Vow To Thee My Country. When we reached the hotel the students went straight to bed, while Vesna and I disposed of some wine with Milos and Milivoje.
On Tuesday morning different teams participated in different sporting events, with the Serbians being especially competitive in basketball and volleyball, while some teams and many leaders slept instead. Our students wanted to go sailing; we were put on a 38 foot sailing boat, with two experienced skippers Dimitri and Lefteris, who sail competitively in races around the Aegean Sea. The sea was always important to Rhodes, which lies at a strategic position; the woods that we saw at Petaloudhes were once part of much bigger forests whose trees were used to construct ships. Rhodes and Lindos both have fine harbours. Seven ships from Lindos sailed to the Trojan wars, before Rhodes Town was even founded.
We all had a turn at steering the boat, which had an impressive array of digital equipment for navigation. We sailed around the northern tip of the island from the harbour at Rhodes Town, and down the west coast, before turning around and returning to harbour. It was a very peaceful (and sleep inducing) trip, spending a couple of hours away from the bustle of life on the land. It was mostly sunny, there was a fresh breeze, and it was all very enjoyable.
The afternoon was for sleeping and packing, ahead of the closing ceremony and official dinner that evening, and an early start the following day for departure to the UK. Unfortunately it was rather cloudy, and relaxing on the beach wasn’t such an attractive proposition; for most of the week we had beautiful blue skies, and warm sunshine.
Tuesday evening’s closing ceremony took place outside in the atmospheric Castello in Rhodes Town. Because of the rain, we were under the arches, which was a delightful place at which to have the medals awarded. There was a fine choir, from a specialist music school on the island; the local guide assigned to the UK team, Hermis, is a professional flute player, and he played, as he had at the opening ceremony; a group of dancers in ancient looking flowing dresses performed dramatically in the open, despite the rain. Medallists went up to the stage draped in national flags, and flash bulbs went off. Dominic received his medal with Maria from Italy, and afterwards he handed her all the roses from our team (each person was given a red rose) – very romantic !
After some photos we departed for the official farewell dinner, at the Grand Hotel in Rhodes Town. This was indeed a grand hotel, and there was a swimming pool in the function room for the dinner (but no-one jumped in) ! By now everyone was tired, after some busy days. Our team signed our large flag, and presented it to our guide Hermis. The Kazakhs had departed early, I had originally assumed for the airport, but in fact when we left the room we found them with the Italians and some others watching the Champions League semi-final between Liverpool and Chelsea. We left for our hotel in Faliraki just before the penalty shoot-out.
The UK team went to bed, very tired by now. The Italians stayed up for hours playing cards in the lobby of the hotel, while many leaders and deputies also stayed up. The Serbians were leaving for the airport very early, and Milos wanted to stay up all night. Milos, Milivoje, Vesna, Nikolai, Dan and I chatted for a long time about various things. It was a rare and valuable opportunity to talk to people serious about maths and maths education from so many countries.
In some nations there are specialist schools for maths. In Serbia for example about 300 students in each school year spend their final four years of school at places such as the Mathematical High Schools of Belgrade and Novi Sad, where Vesna, Milivoje and Milos all studied. In Bulgaria 3000 students in each school year attend such schools, in thirty cities and towns. Competitions start in earnest at a young age, and one gets the feeling that people with talent will not be missed by such a system, and will be encouraged and trained, while in the UK perhaps this is not always the case.
There weren’t many girls or women at the Olympiad, although Albania had three girls out of six in their team; only one leader (Greece) and one deputy (UK) were female. We thought about why this might be – boys’ competitiveness or obsessive nature, or a lack of female role models in the subject ?
Dan Schwarz had taught for a while at an international school in Bucharest and was surprised that in the UK system (which was taught there) calculus is introduced without notions of continuous functions and limits. He is used to a more mathematically rigorous approach. Two of the short-listed problems were written by him, and Nikolai said he might well use them for some Bulgarian selection tests. One was very difficult indeed, getting a jury rating of 27 (the maximum possible).
There was much talk about football. There seems to be much more interest in smoking (the leaders from Romania, Bulgaria, Greece and Macedonia all smoked) and football among mathematicians in this part of the world than in the UK. The Romanians, Serbians and Bulgarians seemed to know all the teams in each other’s countries’ top divisions; and they knew all about football in England. Nikolai subscribes to a German satellite channel and watches twenty hours of football every week ! He is a Liverpool fan, and was excited about Liverpool’s progress to the Champions League final. He’d followed the weekend’s results in England, and knew that Manchester United were now five points clear of Chelsea with three games left to play.
The Serbians and Bulgarians were surprised to hear that Vesna and I would be straight back to school on Thursday. It occurred to us that it might be time to go to bed !
The taxis to the airport were on time on Wednesday morning. We said goodbye to the Italians at the hotel and set off. The flight to Athens was on a small propeller plane, together with the Albanian team, and we sat close to many of the Greek organisers, including Theodore Bolis, cracking jokes, mathematical or other, as ever. He has been the Greek IMO leader since 1985, and he had plenty to say about old IMOs. He recalled Terence Tao being lifted up as a small boy in Warsaw with his bronze medal; Terence got a gold medal two years later as a twelve year old, went to university at thirteen, and in 2006 won a Fields Medal for his research. Fields Medals are the greatest prize in maths; up to four are awarded, every four years. At the last five ceremonies at least one of the winners has been to the IMO, including two from the UK, Tim Gowers and Richard Borcherds. One hopes that high school mathematics competitions inspire people to further study in the subject, and help to progress their lives and the subject.
The flight to Athens was in daylight, and we had an excellent view of Greek islands, including Rhodes, which we could now see to be quite mountainous. There were a lot of islands, including some tiny ones. Rhodes is one of the ten largest islands in the Mediterranean, and it offers a range of terrain, from forest to bare rock, from mountain to sandy beach, from the bright lights of Rhodes Town or Faliraki to the charm of Lindos or the quiet of the Petaloudhes valley. 110,000 people live on the island (excluding tourists), with 30,000 in Rhodes Town, but no other big settlements.
We were held up at Athens airport by a three hour delay, but it gave us a chance to hear about Freddie’s experiences last year at the International Chemistry Olympiad; he will be in the team again this year. Dominic said that he’d attempted forty past Balkan Mathematical Olympiad questions, and the experience was helpful in solving the competition problems this year. Practice does make people better at these competitions, and hopefully the six from our team will work hard over the summer to put themselves in an excellent position to reach the IMO team next year, if not this.
Vesna and the team filled me in on what they had done while I had been away from them with the jury, and eventually we returned to Heathrow to be met by Freddie’s mum and Alison’s dad, while three of our team headed for buses, and one (Preeyan, with the shortest journey) for a taxi. Vesna and I took the tube.
Our team prepared properly for the event, and performed well. The six of them worked well together, and acted as a real team. They were fine ambassadors for the country, socialising with other teams, especially ones that spoke good English (such as Italy and Serbia). My thanks to Ian, Tom, Freddie, Preeyan, Dominic and Alison for making the event a success for the UK on all fronts.
Vesna also made everyone’s work considerably easier, by making arrangements (instructions to the team, insurance, sorting out the T-shirts, etc.) before we travelled, by looking after the team in Greece, and by working very hard on the marking and co-ordination. Her contact with the Serbians and Bulgarians also made it easier for me to make their acquaintance. Things would not have run so smoothly without her.
I will have many peculiar memories of the Olympiad. The only other guests at our hotels seemed to be sixty-five year old Germans in tour groups, who entertained themselves at meals with a trumpeter and a choir. Freddie, Ian and Tom were the only members of our team to brave the cold waters of the sea for a swim, and Freddie apparently relished the prospect. Our team seemed always to be too late at hotel reception to pick up the tennis equipment, but when we returned from sailing, before the other teams had got back from their sport at Rhodes College, they wasted no time, and were in luck.
There was a bizarre moment at the opening ceremony when pictures of the Dodecanese islands, one by one, were displayed on the big screen, with a caption of the name of the island, while a commentary in Greek was given about each island. The only part that was translated by the translator was the name of each island (which was on the screen already !). Then there was Iurie Boreico, Moldova’s gold medal machine, who took his lap top computer on bus journeys and played loud Moldovan rock music for everyone to hear. The fourteen year old Serbian boy’s mother Magda was quite a character, complaining vigorously the night before the contest paper about the hotel hosting a disco. She and the Romanian leader Dan also showed a lot of interest in our anagrams of United Kingdom.
During the exam, while leaders were waiting to go to their hotels, sums of money were exchanged in a room at Rhodes College : team leaders were paying for their observers’ stays, and pocket money was being handed out to the teams (through their leaders), all meticulously signed for in duplicate. At every opportunity during the week the jury chairman Theodore Bolis ran through his range of maths jokes, about dogs called Cauchy, or contour integrals around western Europe, and other jokes about ladders to success and whatever.
The Kazakhs had flown to Istanbul, then to Dalaman in Turkey, from where they reached a port and got a ship to Rhodes, instead of a plane. The girl from Montenegro (their complete team) arrived in Greece with the Serbians, but the Greeks had no idea that she was coming ! One leader translated the exam paper very quickly without difficulty, except that he had forgotten to translate ‘Problem 1’ etc., and when that was corrected he found he’d also forgotten to translate ‘10 points’ ! Things move along, and Ozgur from Turkey whom I met in Romania two years ago is now a father.
Petar said that his packets of cigarettes cost only one Euro in Macedonia; taxes vary greatly around the world. Theodore Bolis talked about shops in Cuba, where the IMO was held twenty years ago, with different prices for locals and foreigners, and about the difficulties of changing money on various trips over the years. People from some parts of the old Yugoslavia now can’t go to other parts without a visa, and Romanian and Moldovan citizens now require visas to visit each other’s countries. The Greeks never referred to Macedonia by that name, but always by its official name of FYROM or the Former Yugoslav Republic of Macedonia. All of this was a window into life in south-east Europe, past and present.
I wish success to this year’s IMO team, at least one of whom will be from this Balkan team. I would like to thank Geoff Smith for inviting me to lead the team to Rhodes, and a host of teachers, mentors and trainers at various camps, who have all helped to train our team. I thank Highgate School for allowing me the time off, and in particular my colleagues in the Mathematics Department for covering my lessons. Vesna would like to do the same for her school, Sevenoaks School. We are of course grateful to the schools of the six students for granting them permission to go. The students enjoyed the trip greatly, especially meeting the other teams, and seeing the ancient sights (and some of the team were classical scholars), as well as competing in the mathematics. I hope that they retain good memories of the Olympiad; I know that I will. In the words of Tom it was, ‘one of the most enjoyable, exciting and eye-opening weeks I have ever lived through’. Greece has provided an excellent Olympiad in a beautiful location; roll on Macedonia 2008, and the best of luck to the UK team there.
Report by Robin Bhattacharyya (leader), with assistance from Vesna Kadelburg (deputy), Tom Lovering (in his unofficial report), and the rest of the team.
Return to IMO Register home page