The International Mathematical Olympiad is the annual world championship of secondary school mathematics. It has been running since 1959 (except for 1980). Teams of six students sit two papers on consecutive days. Each paper consists of three problems, and each problem is worth 7 marks. Thus a perfect score for a student is 42/42. The students are ranked according to their personal scores, and the top half receive medals. These are distributed in the ratios gold:silver:bronze = 1:2:3. The host city of the IMO varies from year to year. Detailed contemporary and historical data can be found at
In 2008 the 49th IMO was held in Madrid. Students from 97 nations participated, and the UK team won four silver medals and two bronze medals. Our rank improved from 29th in 2007 to 23rd in 2008. However, this year we were in a part of the table where the rank statistic was very sensitive. If the team had solved even one extra problem between them, then they would have shot up the rank order. The teams ranked 17th were Romania and Peru on 141 points and the team ranked 24th were Italy on 132. A mark of 15 was required for a bronze medal, 22 for a silver medal and 31 for a gold medal.
The leading three nations at IMO 2008 were China (217), Russia (199) and the United States of America (190). The leading country in the EU was Hungary (10th, 165) and the top Commonwealth performance was Australia (19th, 140).
Contestant P1 P2 P3 P4 P5 P6 Total Award UNK1 Tim Hennock 7 3 0 7 7 0 24 Silver UNK2 Peter Leach 7 1 0 7 7 1 23 Silver UNK3 Tom Lovering 7 1 3 7 7 0 25 Silver UNK4 Freddie Manners 7 2 0 4 7 0 20 Bronze UNK5 Dominic Yeo 5 1 0 7 3 0 16 Bronze UNK6 Alison Zhu 5 7 0 6 7 0 25 Silver total 38 15 3 38 38 1 133 SSSSBB
This was a very solid performance, following on from the United Kingdom team’s winning performance at the inaugural Romanian Master in Mathematics competition
held in Bucharest in February 2008. Only two nations performed better on Problem 5, a gratifying result for the trainers who helped the students to put in a big push to improve our combinatorics this year.
The UK Competitors attended the following schools.
Tim Hennock, Christ’s Hospital, Horsham, Sussex
Peter Leach, Monkton Combe School, Bath, Somerset
Tom Lovering, Bristol Grammar School, Bristol
Freddie Manners, Winchester College, Hampshire
Dominic Yeo, St. Paul’s School, London
Alison Zhu, Simon Langton Girls GS, Canterbury, Kent
Our reserves were as follows.
Jonathan Lee, Loughborough Grammar School
Craig Newbold, Whitley Bay High School
Preeyan Parmar, Eton College
There were two new faces in the side. Freddie Manners has been frittering away his youth by going to non-mathematical olympiads, and Peter Leach is a rower who is trying to extend his range of interests.
I can also report that our notional competitors, Max and Min, would have respectively scraped a gold medal with 32, and secured no reward at all with 13 points (and a dishonourable mention for solving no question completely).
The adults accompanying the UK team were as follows.
UNK7 Dr Geoff Smith, Leader, University of Bath
UNK8 Dr Ceri Fiddes, Deputy Leader, Stowe School
UNK9 Dr Vesna Kadelburg, Observer B, Sevenoaks School
UNK10 Ms Jacqui Lewis, Observer C, St Julian’s School, Carcavelos, Lisbon
The schedule for future IMOs is that the event will be held in Bremen, Germany in 2009, in Astana, Kazakhstan in 2010, in the Netherlands in 2011 and in Argentina in 2012.
Problem 1. An acute-angled triangle ABC has orthocentre H. The circle passing through H with centre the midpoint of BC intersects the line BC at A1 and A2. Similarly, the circle passing through H with centre the midpoint of CA intersects the line CA at B1 and B2, and the circle passing through H with centre the midpoint of AB intersects the line AB at C1 and C2. Show that A1, A2, B1, B2, C1, C2 lie on a circle.
Problem 2. (a) Prove that
![]()
for all real numbers x, y, z, each different from 1, and satisfying xyz = 1.
(b) Prove that equality holds above for infinitely many triples of rational numbers x, y, z, each different from 1, and satisfying xyz = 1.
Problem 3. Prove that there exist infinitely many positive
integers n such that n2 + 1
has a prime divisor which is greater than ![]() .
.
Problem 4. Find all functions f : (0,∞) → (0,∞) (so, f is a function from the positive real numbers to the positive real numbers) such that
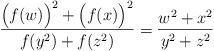
for all positive real numbers w, x, y, z, satisfying wx = yz.
Problem 5. Let n and k be positive integers with k ≥ n and k − n an even number. Let 2n lamps labelled 1, 2, …, 2n be given, each of which can be either on or off. Initially all the lamps are off. We consider sequences of steps: at each step one of the lamps is switched (from on to off or from off to on).
Let N be the number of such sequences consisting of k steps and resulting in the state where lamps 1 through n are all on, and lamps n + 1 through 2n are all off.
Let M be the number of such sequences consisting of k steps, resulting in the state where lamps 1 through n are all on, and lamps n + 1 through 2n are all off, but where none of the lamps n + 1 through 2n is ever switched on.
Determine the ratio N/M.
Problem 6. Let ABCD be a convex quadrilateral with |BA| ≠ |BC|. Denote the incircles of triangles ABC and ADC by ω1 and ω2 respectively. Suppose that there exists a circle ω tangent to the ray BA beyond A and to the ray BC beyond C, which is also tangent to the lines AD and CD. Prove that the common external tangents of ω1 and ω2 intersect on ω.
The problems were proposed by Russia, Austria, Lithuania, South Korea, France and Russia respectively.
This annual diary is loosely based on reality, and would be unsustainable in a court of law. Inevitably this diary tends to focus on things that went wrong (for comic effect), but this should not detract from the overall truth that this IMO was a triumph. We had really good exams and they were marked fairly.
The 49th IMO in Spain was a great success, and this is primarily due to the generosity and energy of our Spanish hosts. The vast IMO local organization is invisible to participants. There are hundreds of them, but you only get to meet a few. This is a shame.
We fly out to Lisbon for a pre-IMO camp. A Portuguese resident, Jacqui Lewis (UNK10 and Observer C), has kindly arranged a camp there for both the UK and Australia. We are staying in a private hotel, taking our lunch and examinations in St Julian’s School, Carcavelos, and dinner at beach restaurants. The school, its students and their parents prove to be extremely hospitable for which many thanks, especially to our expert translator Marianne.
The Australians start to arrive in the morning, in the form of the leader Angelo di Pasquale and six students. In the afternoon the deputy Norman Do and the Observer B Denise Lin also turn up.
The first exam. The Australians win. I am traumatized. Last year in Hanoi Peter Taylor of the Australian Mathematics Trust proposed to donate a trophy called the Mathematics Ashes for an annual competition between the United Kingdom and Australia. He and I agreed the details. One of the later exams at this camp will decide which country is to be the first holder of the urn. This arrangement is based on that which pertains for cricket, whereby Australia and England compete to hold ‘The Ashes’. A funeral urn holds ‘The Ashes of English Cricket’, the burnt residue of some cricket items which were set on fire in the nineteenth century. For our mathematics competition, we have agreed that the scripts of the 2008 losing team will be burned and placed in an urn for all time. Details and photographs are at
http://www.amt.edu.au/news02.html,
at least for now.
Angelo has recognized that he is not worthy to transport the urn from Australia to Europe, and this task is delegated to a courier company. Terry Tao has been blogging about this competition, and the Australian media have become very interested. This is, of course, the way forward for Australian mathematics. Once mathematics is regarded as a competitive sport rather than an academic subject, there will be no limit to the resources made available to support it in Australia.
Today I catch a flight from Lisbon to Madrid to join the jury. A lady called Linda has fallen from the pages of Hemingway and drives me to the airport. She is an American, but a life spent in Portugal has given her soft Iberian edges. She has gone native to the extent that she warns me of the dangers of travelling to Spain, a place which she views with serious suspicion.
At Lisbon airport Easyjet has laid on a pretty good check-in queue, and I set about enjoying it. Eventually my bags and their owner shuffle to the front where I am sharply scolded for putting my bag on the luggage belt too quickly. I must watch that, as I do not wish to cause offence. The check-in lady has an animated conversation with other check-in staff before eventually she waves me forward to engage in the intimate phase of our relationship. It is now clear that she is feeling guilty for admonishing me for promptness, and starts to explain what a difficult day she is having. It seems politic to ignore the hundreds queueing behind me, and focus on her troubles. Eventually my bag disappears and I clutch the precious boarding pass.
I have lunch while waiting for boarding. I order a black coffee and get a coke. Actually in the heat it seems a better idea. I follow the instructions and go to the correct gate and settle down. Time passes and nothing happens. Then suddenly a whole plane-load of people join the queue. I check the screen and discover that they are going to Paris. Now either Paris has moved, or my plane has got lost. I soon discover that my plane has been assigned to another gate. There has been no announcement to this effect, and foolishly I am concerned that time is now short. I rush to the new gate to discover hundreds of better informed passengers in a well-developed queue. We are all off to Madrid but the plane is late. Perhaps you are getting the hang of this now.
Eventually I board. Every seat on the plane is taken, but the flight is short. Spain looks brown. The landing in Madrid is not bad. I retrieve my luggage and walk boldly through the arrivals gate expecting to be met by a throng of IMO aides. Usually teams of enthusiastic helpers usher you to a seat and bring you water. You embrace the local organizers, and pump the hands of other newly arrived team leaders, and the air fizzes with bonhomie, human warmth and the sense of relief that comes at the end of a lonely journey.
Not this time. I look at the handful of sullen taxi-drivers holding up placards and check them individually in case I am their prize. Unfortunately the answer is no. There is a sign pointing to an information desk and a meeting point. After a few minutes I decide to go there. The information lady knows nothing about the IMO, and the meeting point is deserted. I wait, half-expecting tumbleweed to be blown along the corridor. I return to the arrivals area in the hope that the greetings party will have arrived. No chance.
By now I was convinced that I had done something very stupid. The IMO of 2008 is definitely to be held in Madrid, and that is certainly my location. Wearily it dawned that I must have arrived on the wrong day. I check my mental calendar, and persuade myself that I have messed up. I should have arrived tomorrow. The solution seems obvious; check-in to a hotel and return to the airport next day. However, there remains the remote possibility that the greetings party has been kidnapped by space aliens, but that surviving groups of IMO organizers might be present elsewhere at the airport.
I return to the information desk, and explain that I wish to visit the arrival halls of each of their terminals in sequence. I am given an algorithm, and set off in search of these oases of hope. Eventually I find the arrivals area of the next terminal, and locate a nice lady seated next to an IMO notice. Hooray! Apparently there was supposed to be someone to greet me at my terminal, but for some reason this did not happen.
I settle down to await a critical mass of leaders. When we have enough we are escorted to a taxi. The driver tells us we are going to Segovia, and that the journey will take 90 minutes. We cut through Madrid, and then head for the mountains. Our hotel is in the grounds of La Granja Palace de San Ildefonso, Segovia. Just before we arrive, the taxi stops because the Latvian observer is feeling unwell. Immediately our Eastern European fellow passengers light cigarettes, presumably because they think this will help. After a mint her disposition is restored, cigarettes are regretfully extinguished, and we arrive at the hotel five minutes later.
My room is excellent and the facilities are splendid. A very short walk to a second site, the convention centre, takes me to supper and first sight of the jury. As expected, the leader of New Zealand has lost his moustache, but otherwise they seem undamaged. After dinner I get hold of the IMO shortlist and set to work.
We are all working on the problems today. In the evening the solutions are issued. The immediate concern is the geometry problem classified easiest by the Problem Selection Committee, G1. This is invariably selected, so it is very helpful if it is a good question. It concerns a circle manufactured from a triangle, its circumcentre and orthocentre. I had solved it immediately by use of a parallelogram trick. However, I was not worried that the problem was too easy because it was there to test the less experienced students, and they would surely not spot that method. There are other smooth ways to dispose of the question, but the bunnies are not going to spot those either. No, they are going to (a) identify the centre of this circle and (b) calculate its radius using a trigonometric slog. Some will fall by the way and be crushed underfoot. Thus the problem will have some value.
We will find out later that this circle was discovered by Droz-Farny, I realise and that the parallelogram proof works for any pair of isogonally conjugate points instead the ones in the problem. I feel dim for not spotting that first time. I know a thing or two about Droz-Farny lines
http://forumgeom.fau.edu/FG2007volume7/FG200702index.html
but until now his circles had been a closed book to me. The jury decided a few years ago that they would be happy to relax the originality requirement for Problems 1 and 4, because of the difficulty of inventing genuinely new easy problems. The word ‘easy’ is being used here in a relative way. It means that the top six students from a large well-trained country will probably be able to solve such a problem.
The jury meets and begins to discuss the shortlist. We are blessed with another very good jury chair, one Carlos Andradas Heranz. He seems thoughtful and very fair. The jury is used to Maria Gaspar as the face of Spain, and her presence is reassuring.
Several question proposals are thrown out because they are recognized as known. This is very irritating because of the time people have wasted working on the questions, and because our choice is now more restricted. I make the first speech in which I parrot some ideas which I stole from the absent Angelo di Pasquale, the leader of Australia. I acknowledge his contribution, but the speech goes down very well and I appear to be getting the credit. I make a note of this and decide to pinch more of Angelo’s ideas in the future.
Discussions and problem selection proceeds apace. I am seated at the back. Political developments mean that I am no longer inserted between the Ukraine and the United States. This is because of the arrival of the leader of the United Arab Emirates. Thus Ukraine’s Sergiy Torba no longer sits on my left, but instead I have a new friend called Juma Rashed Ali Al Shamisi, or Juma for short. His name is so much more impressive than mine that I feel distinctly inferior. I will look into ways to upgrade my name.
We first select an algebra question as the relatively easy problem to go with the inevitable G1. It is a functional equation question which falls naturally into two parts. This will help to fragment the marks. We then pick a distinctly classy number theory hard problem and a corresponding geometry problem. Neither seems completely impossible. The Italian leader Roberto Dvornicich is a number theorist, and he shows us a quick and elegant proof to that question. The geometry question is an extension of the result that a line drawn through a triangle vertex and the ‘top’ of its incircle hits the opposite side at the contact point of the excircle. The trick with the toy version is to enlarge from the vertex. An extension of that idea will solve this IMO problem.
It remains to discuss the medium questions. At least one must be combinatorial, and neither can be from the geometry list. We move a question from the geometry list to the combinatorics list because (a) that is where it belongs and (b) it gives us more scope. There is a combinatorics question involving switching lamps on and off. There have been no lamp manipulation problems set in recent years, so it gets selected, along with an inequality which, like the other algebra question, falls into two parts.
Along with all this happy progress, there is the bad news that the students and deputy from Pakistan are having difficulties getting visas to attend the IMO. The Pakistan leader is present, but the youngsters are not. The Spanish organizers are working the phones frenetically to Islamabad and to relevant Spanish ministries, but they are given little reason for optimism. This is a most unwelcome development. It seems that the visa applications for Pakistan’s IMO team have become embroiled in ponderous Schengenland protocols. Not allowing students to travel to participate in the IMO must give a terrible impression to the students, their families, teachers and supporters. The Spanish organizers offer to invite the six students from Pakistan to visit Spain later in the year. Whatever the ultimate cause of this incident, it was no fault of the IMO organizers.
An election for the advisory board is very closely fought. Three excellent candidates are standing for one position, and it therefore comes as no surprise that the winning margin of the victorious candidate is small: one vote allows Gregor Dolinar a seat on the IMOAB. In some sense this must be a reward for the excellent way in which he chaired IMO 2006 in Slovenia.
Today the students are scheduled to arrive in Spain. The IMO really starts when the youngsters land. A high-tech display is projected in the coffee area in order to worry the leaders. It displays inaccurate information for most of the day. Two of our party were supposed to arrive at breakfast time by train, but there is no acknowledgement that this has happened even by late afternoon. This concerns me until I notice that implausibly few students have arrived, and that the information given in the display is worthless.
The English language committee meets. We work hard, and produce proposals and options for the full jury to consider. The English language committee is my annual opportunity to strut the boards. The protocol is that Michael Albert and I ponder the wording overnight, then we meet at breakfast to agree a common position. We take our common document to the English language committee as a basis for discussion. Michael Albert works double time managing the data projected on the screens, while simultaneously producing new versions from time to time. We try to encourage all troublemakers to attend the ELC, to tie them in to an agreed formulation. The idea is that when later we take proposals to the full jury, all the firebrands and demagogues will have become tied to the ELC’s wording, and anyway they should be getting tired of complaining about the wording by then, and they will be wanting to complain about other things instead.
This does not work in 2008, because the Dutch leader, dear Quintijn Puite, views the jury session on the English wording as an opportunity to revisit every issue where he didn’t get his way in the ELC (and some where he did). I slap him down brutally, and teams of Spanish psychotherapists are attempting to reconstruct his personality even as I type.
The ELC recommendations are mostly accepted in the end, but the ELC’s alternative formulation of Problem 6 is not adopted, and this will have consequences.
The jury piles into buses, and we set off for Madrid and the opening ceremony. The event is held in a circus. I am able to exchange deranged waving with the rest of the United Kingdom Team. Tom has his understated look, and wears both a Panama hat and a Union Flag. The parade of the nations is attenuated, which had both advantages and disadvantages. Certainly it kept things shorter than usual. The officials and politicians were also admirably restrained. Then the circus entertainment could begin. It had several good acts and one weak one. The clowns were not to my taste. A nice lady with thunder thighs lays with her legs in the air, using her feet to spin and juggle with an axle which has flaming wheels on its ends. Then there is some acrobatic totty which dangles from a great height with only feet tangled in net curtains for support. To finish off, a bunch of male strippers gets half way through their act before morphing into a strongman act. Then they stand on one another a lot, and finish by making a human tower out of the transitive closure of the one-armed handstand. The blokes present are confronted with a rather stark demonstration of their own physical limitations. We had better stick to mathematics then.
Today we complete the business of translating the examination papers into over 50 languages. We also have meetings with the six Problem Captains who propose marking schemes for the problems. The jury suggests modifications, many of which are accepted and included into the official marking schemes.
On the first morning of the exam the Spanish organizers demonstrate their fancy internet software for handling students’ queries. All information is projected for the jury to see and consider. There are just seven questions from the students, and the system worked beautifully. As usual, a few students asked ‘what is the orthocentre of a triangle?’. The jury wisely did not use my proposed answer ‘the isogonal conjugate of the circumcentre’.
Most of the jury go off on a tour, and I repair to my executive suite for a sequence of baths and siestas. In the evening the more robust leaders return from their excellent trip, and the students’ scripts arrive. I am not happy, because two of my students have thrown away marks on Problem 1 by carelessness. Also another student has made a slip on Problem 3 which means he will get only part marks, but he has all the ideas for a full solution. I remind myself that since I don’t have to try to solve these problems under time pressure, it is not fair to criticize those who do. Then I chew some more cutlery.
On the second morning of the exams the jury gathers once again to field the questions. It quickly becomes apparent that the quiet times are over. We are deluged with questions from the students. There are really just two different questions, asked over and over again in all the languages of the world. Although the questions superficially take many forms, they are almost all rephrasings of the following two possibilities:
(a) Problem 5: when considering a sequence, does order matter?
(b) Problem 6: I cannot draw the diagram. Can you help me?
The answers are, of course, yes and no respectively.
The software and jury protocols which worked so well on day 1 now become overwhelmed. I had the pleasure of spending several hours in Heathrow Terminal 5 on its opening day, and there were parallels. We managed to clear the backlog of students’ questions after a couple of hours. That is rather slow.
As you know, I am completely immune to human vice, and a smug thought never crosses my mind. However, the English language committee did point out to the jury that (b) was an accident waiting to happen, and suggested an alternative formulation of the problem which was phrased so as to constitute a kit for drawing the diagram. The jury decided that people trying for 7/7 on Problem 6 would be able to draw the diagram using the original formulation. This was correct, but I suspect that the jury seriously underestimated the volume of whimpering, dull moaning, and grovelling that would be generated from students who were never going to get 7/7 for this.
Finally the question session finishes, and the jury checks out from its luxurious premises. We move to a Madrid hotel. Now, Madrid is a seriously hot place, and one can see the advantages of reducing the area of a hotel’s windows with a view to diminishing the need for air-conditioning. This excellent idea has been taken perhaps a little too far, and the architectural influence of Josef Fritzl is apparent. In future we will have vitamin D tablets in our first-aid kit.
I meet the UK deputy Ceri Fiddes and our Observer B Vesna Kadelburg. They have been elsewhere in Madrid for the past few days. We settle in for the co-ordination phase, and divide up responsibilities. I take the geometry problems. Ceri and Vesna have the rest. We operate a system whereby we have two people expert on any one problem. Ceri is definitely the lady with the lamps (Problem 5) because of her Champollionesque abilities to decipher combinatorial arguments written in the style of Finnegans Wake, the preferred medium of British students. In fact our students have done very well on this question, and it is only UNK6 Alison Zhu’s solution which may need close textual analysis. We enlist Michael Albert of NZ to assist, since he is a professional combinatorialist. He slices through her script in a few minutes, and explains to us that she is actually quite correct. Ceri writes out a careful clean version just in case, but this year the vast majority of the co-ordinators are excellent, and Ceri will not have to make a detailed case to collect Alison’s 7/7.
Vesna has some uncontroversial work to do. My geometry is all straightforward except that I get into a tangle with the co-ordinators of Problem 6, of which more later. I am scheduled to co-ordinate the relatively easy geometry question, Problem 1, on the second day of co-ordination, but the process rapidly gathers pace, and the co-ordinator from our Problem 1 table approaches me a day early. She asks if we are ready to deal with Problem 1 at short notice. I reply 777755. She nods. I go off to to fetch V & C to regularize the position.
Problem 6 presents more difficulties. Four of our students have handed in worthless scripts. UNK2 Peter Leach gets a grudging mark for giving a correct geometrical characterization of a key point in the diagram, though he uses an interrogative form of delivery designed to provoke suspicion in co-ordinators. Instead of saying ‘X is true’, he writes (following the style of our trainer Kevin Buzzard) ‘Can X be true? Wow, yes, I think it is true. Incredible. This is amazing.’ [Translated from the original Leach.]
More difficult still is the script of UNK3 Tom Lovering. He has spotted how to do the problem. However, because he spent so long on Problem 5, it turns out that he has only addressed Problem 6 for a few moments. He has quickly scribbled down in one sentence a correct method to solve the problem, describing a couple of hometheties (enlargements) which, if deployed correctly, tell you everything. Of course he has not had time to write out a proper solution, but he has presented a kit for solving the problem. It will eventually earn 0/7, after appeal to the chief co-ordinator and several meetings. The co-ordinators are defending a marking scheme which I regard as unsuited to this script. However, they will not budge. We find ourselves in alliance with the leader of Montenegro which is in a similar position. Vesna’s language skills come to the fore, and her fluency in what she calls Serbian opens up a new social dynamic for UK leaders. Other people call very similar languages Croatian, Montenegrin and Bosnian.
The real problem goes back to the phase when the marking schemes were presented to the jury by the Problem Captains. For some reason, the scheme for Problem 6 was not presented until very late. The shortcomings of its proposed marking scheme were pointed out forcefully, but it was not modified. In fact two countries were eventually so unhappy with the marks that they were offered that they took the matter to the final jury.
In my view the jury will have to take more responsibility in future. There is typically far more experience in designing IMO marking schemes among the jury than among the co-ordinators. I can think of several questions which have had poor marking schemes since I became UK leader in 2002. This is not because of any ill will or malice on behalf of the Problem Captains (not in Spain certainly), but rather a lack of experience, or perhaps a determination to impose uniformity at the expense of natural justice.
The jury must take responsibility, and when we are asked to approve a defective marking scheme, or even a scheme which needs more study, the jury must say no. I can feel an opening speech at IMO 2009 coming on.
As the marking phase ends, I get to see more and more of our students. This is a happy time. Concerning the physical arrangements for sitting the IMO, our student UNK1 Tim Hennock remarks that the sloping desks are an unnecessary additional hazard, and suggests that in future choosing μ ≥ tan θ would make things easier.
The UK students have been accompanied throughout by a dedicated minder in the form of UNK10 Jacqui Lewis of St Julian’s School. The teams of students have been scattered across central Madrid at seven halls of residence, and the facilities vary slightly.
Our students seem to be in good shape, and Jacqui has clearly cared for them well. The British students are full of robust opinions on IMO organization which I will not echo in this report. From what I hear they will not have been very popular with the hosts. As you move around the world, attitudes towards (and expectations of) young adults vary widely.
At this point we organize the creation of grey residue to be placed in the Peter Taylor Urn, the trophy of the Mathematics Ashes. This involves burning some scripts, and of course we take the matter of safety extremely seriously. It turns out that by some statistical fluke, Australia have won the inaugural Mathematics Ashes. In an act of characteristic duplicity, and in the spirit of Douglas Jardine, the great proponent of Leg Theory, the United Kingdom arranged that Australian mathematics scripts were also burned and so became part of the grey residue which will inspire generations to come.
The closing ceremony is held in university buildings outside Madrid. Just as the gongs were handed out by the Princess Royal in the UK, and by the Crown Prince in Japan, we have their Royal Highnesses the Prince and Princess of Asturias. The Prince’s English accent is immaculate, and our student UNK6 Alison Zhu collects her silver medal from him, thanks to some quick counting and repositioning by the ever chivalrous UNK5 Dominic Yeo.
A short walk takes us to an alfresco banquet enjoyed by all. As usual, the official jury scorekeeper, Rafael Sánchez Lamoneda of Venezuela has kept an accurate record of jury speeches, and the coveted Microphone d’Or is presented to the most garrulous juror. My victory in 2006 is but a fading dream, and the Romanian Leader Radu Gologan’s win of 2007 is also a distant memory. The new champion is the leader of the Netherlands, Quentijn Puite.
Thanks are due to the army of trainers, helpers and administrators who sustain the UK effort at this competition. I also acknowledge financial support from Her Majesty’s Government, and the close and fruitful co-operation between the British Mathematical Olympiad and its parent body, the United Kingdom Mathematics Trust.
The British Mathematical Olympiad now engages in a wide range of regular activities in addition to our national training camps. We have a joint camp with Hungary over the new year and a pre-IMO camp with Australia. We compete as a guest nation in the Balkan Mathematical Olympiad, and were one of the nations taking part in the inaugural Romanian Master in Mathematics competition. These activities enable a large number of students to participate, not just the six students in the IMO team. We have also invited overseas students and trainers at our camps in recent years. I hope that all of these projects will flourish, and that more will be created.
Dr Fiddes hands the Deputy Leadership to Dr Kadelburg. Ceri will now take on the relatively trivial task of becoming Head of Mathematics at Millfield School, and so running the largest mathematics staff of any school in the UK. Thank you Ceri, and to the team, reserves and Observers of 2008.
Geoff Smith UNK7
Return to IMO Register home page