The 26th Balkan Mathematical Olympiad
Leader’s Report
The 26th Balkan Mathematical Olympiad was held from
28th April to 4th May 2009 in Kragujevac,
Serbia. The 6 members of the UK team were
| Chris Bellin | Queen Mary’s Grammar School, Walsall |
| Luke Betts | Hills Road 6th Form College, Cambridge |
| Joseph Briggs | Kennet School, Berkshire |
| Nathan Brown | Camp Hill School for Boys, Birmingham |
| Ruth Franklin | Manchester High School |
| Sean Moss | Havering Sixth Form College |
and the leaders were Vesna Kadelburg of MPW Cambridge and Robin
Bhattacharyya of Loughborough Grammar School. All the students were
17 years old. The trip was kindly sponsored by Winton Capital
Management.
As always, the Balkan Olympiad is a great experience for the
students, most of whom have never participated in an international
competition before. It is a friendly event, less formal than the
International Mathematical Olympiad, although in recent years it has
been expanding with new Balkan countries joining as official members,
as well as an increasing number of guest teams. This year, there were
twenty participating teams: member countries Albania, Bosnia and
Herzegovina, Bulgaria, Cyprus, Greece, Macedonia, Moldova, Montenegro,
Romania, Serbia and Turkey, and guest teams from Azerbaijan, the City
of Brno from Czech Republic (twinned with the City of Kragujevac),
France, Italy, Serbia B, Tajikistan, Turkmenistan, UK and
Uzbekistan.
The exam last four and a half hours and consists of four problems,
traditionally one in each of algebra, combinatorics, geometry and
number theory. Here are the problems.
-
Solve the equation
3x − 5y = z2
in positive integers.
-
Let MN be a line parallel to the side
BC of triangle ABC, with
M on the side AB and
N on the side AC. The lines
BN and CM meet at point
P. The circumcircles of triangles
BMP and CNP meet at two distinct
points P and Q. Prove that
∠BAQ = ∠CAP.
-
A 9 × 12 rectangle is partitioned into unit
squares. The centres of all the unit squares, except for the four
corner squares and the eight squares sharing a common side with
one of them, are coloured red. Is it possible to label these red
centres C1, C2, …,
C96 in such a way that the following two
conditions are both fulfilled
- the distances C1C2, C2C3,
…, C95C96, C96C1
are all equal to
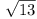 ,
,
- the closed broken line
C1C2…C96C1 has a centre of
symmetry?
-
Denote by S the set of all positive integers.
Find all functions
f : S → S such that
f(f(m)2 + 2f(n)2) =
m2 + 2n2, for all
m, n ∈ S.
Tuesday, 28th April: Arrival day
The trip started smoothly enough, with everyone arriving at
Heathrow on time, despite delays on the London underground. At the
check-in we are told that the flight has been delayed for 3 hours and
are given £5 food vouchers each, so we spend the time having
lunch and playing cards. After a couple of hours we pass through
security and are suddenly rushed to our departure gate. We had just
enough time to get some duty-free presents for our guides. After some
more confusion about the departure time, we finally take off just
after 4pm and land at Belgrade airport some two and a half hours
later. The organisers have kindly provided transport to Kragujevac,
but we have to wait for the Turkish team to arrive. This means
another two hours at the airport and more card games. We are finally
ready to board the bus at 10pm, but there are further problems. The
luggage compartment is too small, so most of our suitcases are stacked
in the aisle (something that definitely did not feature on my risk
assessment!). Then the bus wouldn’t start, so the students get
out to help push it down the slope. At this point I should mention
that I originally come from Serbia, so none of this seems too strange.
Robin promises to point out anything odd enough to mention in this
diary.
We finally arrive in Kragujevac just before midnight (this is 11pm
UK time). They have dinner waiting for us. I am then taken to
another hotel, about half an hour drive away, and won’t see the
students again until after the exam. Unusually for an international
olympiad, the leaders’ hotel is not as nice as the
students’. This seems to make sense – they will be the
ones doing all the hard work on Thursday, and we will only be spending
two nights here. It is nearly 1am, but I am supposed to look at the
shortlisted problems in preparation for the jury meeting. It is a
shame that I don’t have more time to attempt all the problems
properly, but after a couple of hours I decide that it might be a good
idea to get some sleep.
Wednesday, 29th April: Jury meeting
Today is the main Jury meeting where the leaders discuss the
shortlisted problems and select the four contest problems. As a guest
team we do not get to vote, but can make comments and help with the
formulation of the questions. I am pleased to see that I know several
of the leaders, either from Serbia or from previous olympiads. The
meeting is conducted in English, but the leaders speak among
themselves in a variety of different South Slavic languages, with
another group using Turkish and Russian. I note that Robin would be
fascinated by the linguistic mix.
The problem selection committee inform us that they have received
26 proposals and have selected 19 for the shortlist. The problems
have been split into four groups: Algebra, Combinatorics, Geometry and
Number Theory, and the problem selection committee have designated
each one as easy, medium or hard. The aim is to select one problem
from each group, preferably with one easy, two medium and one hard.
In the first part of the discussion several problems are rejected as
known or relying on university-level knowledge. This leaves us with
just one combinatorics problem which will therefore have to be
selected. It is also proposed that no more than two problems should
come from the same country. This may restrict the selection even
further, although at this stage the identity of the proposers is
supposed to remain unknown.
Next, an algebra problem is selected as problem 4. This should
give us more flexibility in choosing a medium problem. After some
discussion about geometry problems, a vote was taken and one of them
was selected for problem 2. This left us with a relatively simple
choice of an “easy” number theory for problem 1. The
authors of the problems are revealed as Greece (problem 1), Moldova
(problem 2) and Bulgaria (problems 3 and 4). General opinion seems to
be that the paper is quite difficult, but the problems are nice.
We still need to agree the exact formulation of the problems,
before they can be translated into all the different languages. Most
students will get the official English version of the problem sheet,
as well as one in their own language. This is my big moment –
it is a tradition for the UK leader to help decide on the best
wording. There is a lot of input from Dan Schwarz, a Romanian who
used to live in Canada and is one of the problem selectors and
coordinators here, as well as Claude Deschamps and Massimo Gobbino,
the French and Italian leaders. The combinatorics problem is
re-worded several times before everyone is happy with it. There is
the apparently mandatory discussion about how to denote the set of
positive integers (and just why ‘positive’ in French and
Romanian includes zero), resulting in the agreement that the official
version will use the letter S, and everyone can use whichever letter
their students are used to in their national versions.
Once the official version is agreed we can start translating. My
work is not done however, as the statement of problem 3 talks about a
‘centrally symmetric path’, which I need to
‘translate’ as ‘having rotational symmetry of order
two’. To my knowledge, this is the first time that there will
be a UK version different from the official English version. With
this out of the way I join the Serbian leader in preparing his
translation, which will also be used by Montenegro. Students from
Bosnia and Herzegovina can choose from three possible languages, two
of which are identical only written in different alphabets.
With all this work done we deserve a lunch break. Our hosts are
taking their role very seriously and we are taken to a restaurant in a
small traditional village. After the first three courses we walk up
the hill to a local church. It turns out that the guide does not
speak English, so my linguistic skills are put to a test as I attempt
simultaneous translation. The guide is keen to take us all the way to
the top of this volcanic hill, but most of us are not really up to it
after the generous starters and local spirits. Under the excuse that
we need to return to work soon, we go back to the village to complete
our lunch with the spit-roasted lamb. There is some post-meal
entertainment and to everyone’s amusement I am made to
demonstrate a traditional dance with the restaurant owner. Luckily
the Kazakhstan leader is keen to join in.
The rest of the afternoon is spent checking and printing out the
translations. After dinner we all gather in the conference room to
watch football: Man United v Arsenal, Champions’ League
semi-final. People in the Balkans are well versed in all matters
football-related and seem to be particular fans of the Premier League.
The Bulgarian leader is even wearing an Arsenal top. As smoke fills
the room I realise how quickly I have forgotten what pubs used to be
like before the smoking ban. After the match (for the record, Man U
won 1-0 – Robin will be pleased) I work on the problems some
more in preparation for the marking.
Thursday, 30th April: Contest day
We leave the leaders’ hotel and will check in with the
students after the exam. The contest will be held in the First
Kragujevac Grammar school, an imposing building dating from 1887. It
was the centre of Serbian education in the early 19th century. The
opening ceremony is quite short, involving only one government
minister and no folk dancing (all that practice for nothing!).
Students go straight into the exam and we prepare to answer questions.
Even after all the debate about positive integers, several students
ask whether zero is included – I guess it’s better to be
safe. We also receive a question from Joseph about function notation.
On the way back to the hotel Robin and I decide to take a walk around
the town. There is a children’s football tournament going on in
the main square with lots of people watching; once again this reminds
us of the importance of sport in this part of the world.
After the exam Robin brings the students back to the hotel and we
all have lunch together, discussing the problems. Later on we will
talk to each student individually to find out how they think they have
done. Students’ comments can be very useful when marking the
scripts. Several of the team find mistakes and holes in their
solutions, and not many full solutions are claimed, but there are some
good ideas all round. Everyone seems glad that the exam is over and
they can get on with meeting the other contestants.
The third jury meeting is held in the afternoon. The coordinators
have proposed marking schemes for each problem but there is still a
lot of discussion about the details. Everyone seems to have a
different opinion on how many marks should be taken off for not
checking that a certain function satisfies the given equation, and
whether any marks should be awarded for spotting one solution to the
number theory problem. After the amended mark schemes are voted
through the students’ scripts arrive and we are keen to get
marking straight away. Each team’s leaders mark the scripts
according to the marking scheme. Coordinators for each question have
photocopies of the scripts and will suggest marks. Over the next two
days we will meet with the coordinators for each problem and agree the
marks. Our job is to convince them that any omissions or lack of
clarity are ‘trivial’, and possibly find alternative
solutions which follow from our students’ incomplete work.
We will only coordinate problem 2 on the first day, so we start by
marking that. It is geometry, and generally considered quite
difficult. None of our team claim to have solved it, but Chris and
Joseph have done some useful angle calculations. As we are done with
problem 2 quite quickly, we decide to have a go at two more problems,
only leaving problem 1 for tomorrow. We keep being distracted by Dan
Schwarz who has decided that we are working too hard. So we spend
quite a lot of time listening to his stories from Romania and Canada
and despairing over the state of education today, while passively
smoking a packet of Camels. Nevertheless, we manage to mark
problem 3 and most of problem 4 before deciding to go to sleep around
1am.
Friday, 1st May: Excursion and first
coordination
In the morning Robin and the students go on an excursion while I
stay at the hotel to look over the scripts some more. Coordination
will start after lunch. We are not expecting many marks for problem
2, and we are a lot more excited about a football tournament the local
students are organising. After lunch we make our way to the school
where the coordination is taking place. The organisers have set up a
live score board so we can see the latest scores as soon as the
coordination is over. There is already a crowd looking at the first
results.
While waiting for our coordination slot Robin and I decide to look
around the school. The classrooms are quite bare, although we find
some interesting science posters in one. Robin is surprised at the
amount of graffiti everywhere. I reflect on my school days and the
number of poems and random thoughts recorded on school desks. It is
certainly very different from most schools in the UK.
The football tournament is taking place in the gym. Teams of six
should be made up of students from two different countries. It turns
out that only Nathan is keen for football, and the others go off to
play frisbee. Robin and I are more than happy to make up the numbers
in the UK-French team. Before the match starts however, we need to go
off and coordinate problem 2. This was reasonably quick and
more-or-less as expected. We return to the gym just in time for the
game against the Azerbaijan/Turkmenistan team. Despite our best
efforts and Nathan’s goalkeeping skills we lose 4-0, but enjoy
ourselves thoroughly.
We now have the rest of the day to finish marking the other three
problems. Problem 4 should be reasonably straightforward. Nearly
everyone has one mark for proving that the function is injective, but
Chris has also come up with some interesting identities, so there
should be a few more for him. Problem 1 also turns out to be
reasonably clear cut, as everyone’s solutions fit neatly within
the marking scheme. Problem 3 is the most interesting. Luke and
Nathan both thought they had solved it, but failed to consider the
possibility that a symmetric path may consist of two self-symmetric
parts. We spend quite a lot of the evening trying to decide how many
marks to ask for, but eventually go to join the other leaders and
coordinators in the bar. Meanwhile the students have made friends
with everyone and are teaching the Italians how to play Mafia.
Saturday, 2nd May: Second
coordination
Today we will coordinate the remaining three problems. The
students will spend the day sightseeing and playing games. Problem 3
is probably the most interesting. We need to explain some of
Luke’s and Nathan’s arguments in more detail, but
eventually they get the marks. Problem 4 coordinators are very
impressed with Chris’ ideas and award his script 3 points
– the eighth highest score out of the 115 contestants. Problem
1 is our best overall: Luke solved it completely and everyone else
gets substantial marks according to the marking scheme. The
coordination is over reasonably quickly. To our slight
disappointment, we had no exciting arguments with the coordinators,
but it does mean that we have the whole afternoon free to go out for a
walk. The scoreboard is taking its final shape, and it looks like we
may get quite a few medals.
We have several hours to spare until the final jury meeting, so a
group of leaders, deputies and coordinators decide to go for a walk
around the memorial park. The park commemorates citizens of
Kragujevac, including schoolchildren, who were killed in a Nazi
revenge attack in the Second World War. The museum is fairly
distressing, but the park is beautiful. At some point we bump into
the students on their way to a lake several miles away. It’s
good to see that they are being sociable and having a good time.
The final jury meeting is the place to sort out any unresolved
coordination issues and decide on the medal boundaries. There are no
problems with the scores, and the results are officially approved. As
predicted, the scores are quite low. The winner is a 16-year-old
Serbian student with 35 out of 40. Serbia are also top of the
unofficial ranking, closely followed by Turkey and Bulgaria. The
discussion about the medal boundaries takes a while. Although the
rules specify very clearly the proportion of contestants to be awarded
each medal, some leaders are in favour of awarding slightly more,
while others think that the numbers should be decreased. The
organisers point out that there is only a certain number of actual
medals. Eventually the boundaries are set slightly lower than
expected, so we end up with six medals, one silver and five bronze.
Robin and I can’t wait to get back and tell the students. The
jury also decides to award several special prizes to students who
solved the difficult third and fourth problems.
The students are back in the hotel playing games and are delighted
to find out that they all got medals. Our final scores are:
| P1 | P2 | P3 | P4 | total | medal |
|---|
| Chris Bellin | 5 | 1 | 1 | 3 | 10 | bronze |
| Luke Betts | 10 | 0 | 4 | 1 | 15 | silver |
| Joseph Briggs | 8 | 1 | 0 | 1 | 10 | bronze |
| Nathan Brown | 6 | 0 | 4 | 1 | 11 | bronze |
| Ruth Franklin | 6 | 0 | 0 | 0 | 6 | bronze |
| Sean Moss | 6 | 0 | 0 | 1 | 7 | bronze |
Sunday, 3rd May: Excursion and the closing
ceremony
Today is the day of the main excursion. In the morning we visit
the Resava Cave, a large cave with some fascinating formations. It
was only discovered in 1962, but quickly became one of the main
tourist attractions in Serbia and a popular destination for school
trips. We then drive a short distance to the Manasija Monastery,
built in the early 15th century. Inside we find out that
the art of graffiti dates back several centuries – we find names
engraved on pillars, with dates like 1746! The next stop is a
restaurant on a fishing lake. It starts to rain again. Luckily most
of the seating is under a roof, but some of us have to hold an
umbrella in one hand whilst eating the soup. The fresh fish is really
excellent.
As the rain has caused a slight delay, we don’t have much
time to spare before the closing ceremony, held in the school’s
impressive assembly hall. This is again quite brief, with a complete
absence of politicians and folk dancing. Of course, it takes time to
award 88 medals but it is great that all our students get to go up on
the stage. Medals received, we all get on the bus and head for the
closing dinner.
It is not often that one can see a group of young mathematicians
dancing to excessively loud music. But most of our team are on their
feet soon, led by the Serbian guides. Joseph’s hat turns out to be a
particular hit. Even Robin joins in for a bit. I use the time to chat
to my Serbian friends. After the party is over we head back to the
hotel to pack. We are leaving very early in the morning.
Monday, 4th May: Departure day
As we prepare to board the bus just before 6am I find out that the
students had decided to stay up all night. They all seem slightly
dazed, but the suitcases are ready. Well, at least the journey will
pass more quickly if they are asleep. We arrive at the airport with
plenty of time to check in, have breakfast and do some last minute
souvenir shopping. I won’t ever fully understand why it is
important to buy spoons, but the students manage to find some, so
everyone goes home happy.
Vesna Kadelburg
July 2009
Return to IMO Register home page
Contact: Joseph Myers
(imo-register@imo-register.org.uk)
Online HTML version last updated:
5 January 2016
 ,
,