52nd International Mathematical Olympiad
UK leader’s report
Amsterdam, the Netherlands, 16th–24th July 2011
Introduction
The UK competed in the 52nd
International Mathematical Olympiad, in Amsterdam, between the
16th and 24th of July. This is the 44th IMO in which the UK has been proud to
take part. The team were:
| UNK1 | James Aaronson | St. Paul’s School, London |
| UNK2 | Andrew Carlotti | Sir Roger Manwood’s School, Kent |
| UNK3 | Ben Elliott | Godalming College, Surrey |
| UNK4 | Adam Goucher | Netherthorpe School, Derbyshire |
| UNK5 | Josh Lam | The Leys School, Cambridge |
| UNK6 | Jordan Millar | Regent House School, County Down |
The first reserve was Richard Freeland (Winchester College,
Hampshire), and the second reserve was Edward Kirkby (Alton College,
Hampshire).
I (Dr James Cranch, University of
Leicester) led the team; Jack Shotton (formerly of Trinity College, Cambridge, and
soon to be of Imperial College
London) was the deputy leader.
Dr Geoff Smith (University of Bath)
attended, officially in a capacity known as “Observer A”,
but in reality for business with the IMO Advisory Board, who are
responsible for the strategic planning of successive IMOs. Sally Anne
Huk (Bancroft’s School, Woodford Green) came in the capacity of
“Observer C”: a pastoral specialist for our team. A flying
visit was made by Dr Ceri Fiddes (Millfield School) to promote the European Girls’ Mathematical
Olympiad.
Questions
As usual, the IMO consisted of two exams on consecutive days, each
with three questions and each lasting four-and-a-half hours. Each
question has equal weight: seven marks.
Here are the questions (together with their submitting countries):
First day:
-
(Mexico) Given any set
A = { a1, a2, a3, a4 }
of four distinct positive integers, we denote the sum
a1 + a2 + a3 + a4
by sA. Let nA denote the number of
pairs (i, j) with
1 ≤ i < j ≤ 4
for which ai + aj divides
sA. Find all sets A of four
distinct positive integers which achieve the largest possible
value of nA.
-
(UK) Let 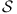 be a finite set of at least two points in the plane. Assume that
no three points of
be a finite set of at least two points in the plane. Assume that
no three points of 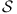 are collinear. A
windmill is a process that starts with a line
ℓ going through a single point
are collinear. A
windmill is a process that starts with a line
ℓ going through a single point 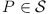 . The
line rotates clockwise about the pivot P
until the first time that the line meets some other point
belonging to
. The
line rotates clockwise about the pivot P
until the first time that the line meets some other point
belonging to 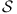 . This point, Q,
takes over as the new pivot, and the line now rotates clockwise
about Q, until it next meets a point of
. This point, Q,
takes over as the new pivot, and the line now rotates clockwise
about Q, until it next meets a point of
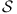 . This process continues indefinitely.
. This process continues indefinitely.
Show that we can choose a point P in 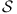 and a line ℓ going through
P such that the resulting windmill uses each point
of
and a line ℓ going through
P such that the resulting windmill uses each point
of 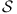 as a pivot infinitely many times.
as a pivot infinitely many times.
-
(Belarus) Let
f : ℝ → ℝ be a
real-valued function defined on the set of real numbers that
satisfies
f(x + y) ≤
yf(x) + f(f(x))
for all real numbers x and y.
Prove that f(x) = 0 for all
x ≤ 0.
Second day:
-
(Iran) Let n > 0 be an integer. We
are given a balance and n weights of weight
20, 21, …,
2n−1. We are to place each of the
n weights on the balance, one after another, in
such a way that the right pan is never heavier than the left
pan. At each step we choose one of the weights that has not yet
been placed on the balance, and place it on either the left pan or
the right pan, until all of the weights have been placed.
Determine the number of ways in which this can be done.
-
(Iran) Let f be a function from the set of
integers to the set of positive integers. Suppose that, for any
two integers m and n, the difference
f(m) − f(n) is divisible by
f(m − n). Prove that, for all
integers m and n with
f(m) ≤ f(n), the number
f(n) is divisible by f(m).
-
(Japan) Let ABC be an acute triangle with
circumcircle Γ. Let ℓ
be a tangent line to Γ, and let
ℓa, ℓb
and ℓc be the lines obtained by
reflecting ℓ in the lines BC,
CA and AB, respectively. Show that
the circumcircle of the triangle determined by the lines
ℓa, ℓb and
ℓc is tangent to the
circle Γ.
Results
The UK obtained 2 gold, 1 silver and 2 bronze medals and 1
honourable mention and a score of 132 out of 252, coming joint 17th
out of 101 participating countries. The medal boundaries were 28 for
gold, 22 for silver and 16 for bronze.
| James Aaronson | 7 | 1 | 7 | 7 | 7 | 0 | 29 | Gold Medal |
| Andrew Carlotti | 7 | 7 | 0 | 7 | 7 | 0 | 28 | Gold Medal |
| Ben Elliott | 7 | 0 | 2 | 7 | 7 | 0 | 23 | Silver Medal |
| Adam Goucher | 7 | 0 | 0 | 7 | 7 | 0 | 21 | Bronze Medal |
| Josh Lam | 7 | 1 | 0 | 1 | 4 | 0 | 13 | Honourable Mention |
| Jordan Millar | 7 | 1 | 1 | 7 | 2 | 0 | 18 | Bronze Medal |
Our team all pulled their weight to beat several extremely worthy
opponents. In particular, this is the first time since 1992 that we
have beaten our friends and training partners from Hungary.
The UK was fourth in the EU, behind reliable strong performers
Romania, Germany and Poland. The Commonwealth of Nations was led by
Singapore, with an extremely strong performance (particularly on the
‘Windmill’ problem 2); Canada and the UK shared joint
second place.
The performance of the top end of the team was extremely
impressive. The last time the UK had two students receive a gold medal
was 1996. However, both are available for selection next year (as are
Adam and Josh): the last time the UK had two students receive a gold
medal who went on to compete the following year was 1975.
Viewing the competition from a less Anglocentric perspective, there
is much to say. The top twenty nations, and their scores, were as
follows:
| rank | score | country | rank | score | country |
|---|
| 1 | 189 | China | 12 | 147 | Japan |
| 2 | 184 | USA | 13 | 144 | South Korea |
| 3 | 179 | Singapore | 14 | 138 | Hong Kong |
| 4 | 161 | Russia | 15= | 136 | Ukraine |
| 5 | 160 | Thailand | 15= | 136 | Poland |
| 6 | 159 | Turkey | 17= | 132 | Canada |
| 7 | 157 | North Korea | 17= | 132 | UK |
| 8= | 154 | Taiwan | 19 | 129 | Italy |
| 8= | 154 | Romania | 20= | 121 | Brazil |
| 10 | 151 | Iran | 20= | 121 | Bulgaria |
| 11 | 150 | Germany | | | |
Only one student in the competition achieved a perfect score, Lisa
Sauermann of Germany. This stunning achievement, together with her
previous three gold and one silver medals, sends her to the the top of
the IMO hall of
fame. I understand that Lisa is now going to Bonn to study
mathematics; her retirement from IMO dominance will inspire mixed
feelings of sadness and relief.
That does not exhaust the good news for girls. At an IMO it is
understandable that many journalists will be following the fortunes of
the home team; this year the top score on the Dutch team was obtained
by another girl, Madelon de Kemp. There is every sign that both Lisa
and Madelon have already become role models for the next generation of
IMO stars.
Leader’s Diary
Saturday, 9th July
I wake up in Cambridge, having had the foresight to position myself
there the night before. Today, we are starting our pre-IMO training
camp at Trinity College; we are holding this jointly with the
Australian team.
I have plenty of time to ablute and do a bit of maths before the
Australians arrive. I greet my counterpart Ivan Guo and his deputy
Graham White with a loud “g’day”; they tell me that
they actually only say this to naive British people.
I mislead them into thinking that they might be able to obtain
breakfast in Hall, but in fact the staff are on holiday, so this turns
out to be just a good excuse to march through some of the
College’s grounds, which must be very invigorating after
twenty-eight consecutive hours of travelling.
After they install themselves in their rooms and shower I take them
to a cafe. We are joined by an early-arriving British team member, the
Northern Irishman Jordan Millar. We then spend the morning walking
around Cambridge. We avoid the very centre, when we discover that a
small racist demonstration will be taking place. Such things really
aren’t normal here: Cambridge is proud to be cosmopolitan, and
the demonstrators are largely football hooligans bussed in from
elsewhere in the country.
Then we pass by Trinity’s hall, again finding it not serving
food. My kitchen connection Alan Queripel sees a fellow Guernseyman in
distress and beckons my team into the staff canteen where we lunch
well on pork chops and raspberries and cream.
After this the rest of our team turn up. This is very helpful: the
main purpose of the day is for our team to familiarise the Australian
team with various British customs which may seem quaint from an
Australian perspective, such as having darkness during the daytime and
sunlight during the night.
Also turning up this afternoon is my deputy, Jack Shotton, fresh
from a week running around the Lake District like an idiot, and our
camp’s extra helpers: combinatorics expert Joseph Myers, and
all-round nice guy Sean Moss.
We explain the logistics of the camp, order takeaway pizza and eat
it outdoors in the sunshine, and then after a few games of cards we
mercifully allow the Australians to sleep.
Sunday, 10th July
The day begins with a makeshift breakfast, then continues with a
practice paper. Then we finally gain access to Trinity College’s
hall for substantial refreshment. We are joined by the Australian
Maths Trust’s head honcho Peter Taylor, who is in transit from
Lincolnshire to London in the middle of a short holiday practising
industrial espionage and visiting relatives.
It turns out that the Australians beat us marginally in the
practice paper (by the margin of 84 to 82); their top individual score
is 21 to our 20. This does not bode well for the Ashes, which are to
be contested on Tuesday.
Paul Russell arrives to give a session, entitled How to find
(and keep) a husband. He was a member of our IMO team last time
the UK beat China, in 1996.
Several games are produced. These include Set, which
inexplicably enough is the only game I know based around combinatorial
lines in a four-dimensional hypercube of side-length three (this game
is also a favourite of the Hungarian team, and we first learned it
from them). We also played the anarchic We Didn’t Playtest
This at All, which shows strong signs of having been
playtested.
I am happy to report that we have an excellent class of parent this
year; Josh’s father arrives to donate a bottle of champagne to
the cause.
Someone passes comment on the similarities in names among the
Australian team. Indeed, four of them have two-letter surnames ending
in ‘u’: Fu, Lu, Xu and Yu. Joseph points out that there is
a story among the British delegation: half of the students have first
names beginning with ‘J’, and also half of the adults
travelling out on the 12th, and also half of the adults travelling out
on the 16th, and also half of the extra pre-IMO camp staff (Joseph vs
Sean). It’s exactly like the Belgian system, which chooses a
half-Flemish, half-Walloon team each year.
Monday, 11th July
After breakfast in hall, it is clear that the teams are settling
comfortably into the idea of getting up in the morning and doing a
four-and-a-half-hour exam. This is a good habit to get into, when
preparing to sit an IMO.
We decide to take the students punting. For foreign readers, this
is a popular student pastime in Oxford and Cambridge, where a small
heavy-bottomed wooden boat is propelled along an inland waterway by
the expedient method of repeatedly poking the riverbed with a long
pole. Jack and I are old-time masters at riverbed-poking; some of the
students (and Australian adults) take to it better than others.
Then we are visited by Prof Tim Gowers FRS, nowadays better known
for his Fields Medal than for his IMO perfect score from 1981. His
decision is to ensure that the teams are well-versed in the basics, by
teaching them how to multiply and divide: it is much appreciated.
We mark the morning’s paper. The UK’s combinatorial
supremacy has caused them to comfortably outpoint the Aussies on the
crucial Q2. Several contestants have produced nasty recursive
arguments with dubious notation but the underlying ideas are
first-rate.
Adam’s script goes further and makes the inspired move of
working in two dimensions where things are much clearer and admit a
commonsense geometric interpretation; the downside is the use of some
baroque terminology he must have found on Wikipedia one sleepless
night. We both praise him and encourage him not to assume his readers
have an intimate familiarity with tabloid mathematics.
Then there is a smart dinner in Hall, kindly organised by my
predecessor Imre Leader, and equally kindly hosted by Tim Gowers. The
UK team’s uniform has not arrived yet, so they must make do with
chinos and polo-shirts; the Australians are resplendent in their green
blazers.
All the students march in. Naturally they clump together, UNKs at
one end and AUSes at the other, to engage in mutual distrust and
enmity. We protest, finding an algorithm to permute them, and the
dinner is a much more pleasant affair for it; I enjoy the company of
Adam, Jordan and an Australian, Angel.
After this we have a quick debrief of the morning paper, in which
Joseph explains that, just before he sat his first IMO in 1994, he had
been corresponding with Paul Erdős on the content of Q1. He
exhibits a letter from the great Hungarian which begins “Dear Dr
Myers…”.
I wish my team well for the IMO and explain what I expect of
them. I will be leaving the next morning and things will be hurried
then.
Tuesday, 12th July
After breakfast, the Ashes begin. This is our annual contest
against the Australian team, decided on the basis of a single
IMO-style paper.
I remain long enough to see the students knuckle down to it, give
the IMO first aid kit and a few euros to Jack, and leave for the
IMO.
The railway network carries me to London Gatwick airport
uneventfully. On the plane I get chatting to an intensive care nurse
who frequently visits Amsterdam. Upon entering the arrivals area she
ushers me away from the vast hordes of easyJet customers we flew in
with, through several cafes’ worth of seating, to an apparently
secret, entirely empty passport control room. This gives way
immediately to the baggage reclaim area, from which I can see the long
queues at our intended passport control desks. Thanks, whoever you
are!
My good luck continues when my holdall is the first bag onto the
carousel. I grab it and step out to be met by two beaming Dutch
helpers. They fix me up with a bottle of Schweppes Bitter Lemon, the
taste of the Netherlands, and we mass together at a meeting point
where about six volunteers are hanging around and smiling.
There I meet the Irish delegation: the leader Bernd Kreussler whom
I know from past IMOs, and his observer Mark Flanagan.
There is a bus journey of about ninety minutes, to somewhere in the
vicinity of Eindhoven, in the south of the Netherlands. We arrive at a
hotel of vast proportions: even though it has been divided into
coloured zones to aid navigation, it still seems certain to bewilder
for days.
After this I manage to lay my hand on the object which has brought
me so far: the shortlist. There are thirty problems. Shortlists are
usually good, but this one is extraordinarily exciting, particularly
in the combinatorics department.
I then hang around for a while waiting for my observer, the
Advisory Board member Geoff Smith, to arrive. This means I unwittingly
miss dinner (my mind is still on UK time) but the hotel provides a
fully functional packed meal.
From Geoff I learn the results of the Ashes. It has been a tie, and
so the urn and cup are retained by the British team. Geoff is pleased
with this: the Australians expended the maximum possible effort to not
win back the Ashes. By now, the team will be relaxing with a talk by
Bryn Garrod on the Rado graph.
After some time spent attempting the shortlist, Geoff and I go and
socialise. Old friends come and go, including the local capo di
capi Wim Berkelmans, the IMO computing expert Matjaž
Željko, and the newly-promoted Swiss leader Julian
Kellerhals.
Wednesday, 13th July
I get up early and swim 25 lengths of the
hotel’s convenient pool.
At lunch I sit with some of the Dutch organising staff: onetime
deputy leader Birgit van Dalen is about to be in charge of the student
experience, and Rozemarijn Schalkx has been running the office. I
complain at the large amount of time I have wasted in recent weeks
while exchanging emails with the Dutch IMO organisation, in attempting
to spell the latter’s name.
The model solutions are released. I wait a valiant four hours
before picking them up, and another hour before giving up and looking
at them. Some heavy study is warranted.
My brain becomes confused eventually, and I go for another
swim. Unfortunately, about five minutes in, a gang of middle-aged
Dutch ladies put a divider across the middle of the pool to prevent me
doing lengths, and begin wiggling around to dance music in the deep
end. So I hop out and go to dinner instead.
Afterwards there is a small amount of experimentation with the
beers of the Netherlands and of the neighbouring countries. The
Belgian leader Bart Windels is present, as always with his wife Ria
van Huffel; both are experts in these matters. Bart claims that it is
cheaper to bring Ria to the IMO than it would be to hire a private
detective to watch her for the same period.
Thursday, 14th July
The morning begins with the first jury meeting, at 9am. The chair
of the jury, Professor Hans van Duijn, welcomes us.
In his opening speech he tells us that Eindhoven is thought of as
the country’s “Brainport” (in contrast with
Rotterdam, the seaport, and Amsterdam Schiphol, the airport); also
that it was recently named the smartest area in the world.
We then prepare for the annual bonfire of questions: countries are
expected to declare if any problems are similar to problems they have
seen in the literature. This year is unusually violent: four of the
thirty questions end up discarded for their similarities to
others. Later on, the Indian leader will get carried away and attempt
to destroy the eventual Problem 4, but he won’t succeed.
I find myself with a little while to spare, so get in the pool
again. I am pleased with my 40 lengths, but then discover that the
pool is only 12.5m long. Not so virtuous after all.
We have been invited to a reception and buffet dinner at the
Technical University of Eindhoven, a short bus journey away. We arrive
and are given a drink.
The rector of the university, a certain Professor Hans van Duijn,
gives a short welcoming speech. Firstly he tells us that Eindhoven is
thought of as the country’s “Brainport” (in contrast
with Rotterdam, the major seaport, and Amsterdam Schiphol, the major
airport); also that it was recently named the smartest area in the
world. Secondly, he then gives way to a second speaker.
That second speaker tells us that Eindhoven is thought of as the
country’s “Brainport” (in contrast with Rotterdam,
the major seaport, and Amsterdam Schiphol, the major airport); also
that it was recently named the smartest area in the world. Only now
does Ivan express his surprise to me at learning that you can travel
by brain.
Over dinner we are treated to a fine medley of Andrew Lloyd Webber
and Elton John tunes, and also a string quartet. I chat to the leaders
of several English-speaking countries such as Norway and Finland.
Then it is back to the jury. We must decide the two easy questions
tonight.
An interesting and unusual situation arises. Most years, at the
IMO, there are two geometry problems: one easy, one medium or hard:
it’s become more-or-less expected.
This year there are some extremely pleasant and perfectly
approachable questions in algebra, geometry and number theory. But,
this year, the easy geometry questions seem not to be much loved, and
the much-loved geometry questions seem not to be easy.
There are various impassioned pleas in favour of geometry, which is
perfectly reasonable. However, the shortlist seems to be screaming at
us to do otherwise, and there is evidence that the crowd are in
favour.
A tea break is taken in order to ponder it for a while before a
final decision. The mood is tense.
Then Claude Deschamps, the French leader, approaches me in a
rush. His observer, Johan Yebbou, has found the exact statement of G2,
together with a proof similar to the shortlist proof, in a published
paper in French from 1918.
The Brazilian leader suggests that a student who is familiar with
the French literature from the era of the First World War fully
deserves seven free IMO points. However, the IMO intends to generate
novel and ingenious problems, and it has done so very successfully in
the past, and so the jury votes to squash G2.
The opinion of the problem selection committee is sought; they
state that they consider A1 and C1 to be too easy. The jury
accordingly back exactly those two questions. We have a paper without
any easy geometry!
Friday, 15th July
The next day we start by picking the hard problems. The geometry
lobby gets their way rapidly, and we end up with A6, a nasty
functional inequality, and G8, asking for a proof of a rather elegant
but fearsomely hard theorem in pure geometry.
Then it is time for the medium problems. It is observed that no
number theory is on the paper yet, so a motion passes easily that we
should select one, and the unusual-looking N5 makes it fairly
easily.
Then there is a fight. There is a pro-geometry lobby who think that
one geometry problem in six is not nearly enough and that having two
geometry problems is vital. There is another group who think that a
medium geometry problem will test the same skills as a hard geometry
problem, so will skew the paper. Yet more people feel that the quality
of the combinatorics shortlist questions are exceptionally good and it
would be a shame not to use another. An anti-combinatorics coalition
suggest that almost all of the questions chosen so far have some kind
of combinatorial flavour already.
The choice is whittled down to G4 and C3. There are impassioned
speeches on both sides, and eventually C3 is chosen by the remarkable
margin of 47 votes to 46.
After this, the authors of the papers are revealed. It turns out
that we must blame Geoff for C3.
Then it is time to produce the official English language versions
of the papers. The UK leader is ex officio chair of the
committee; I do not relish this task, but things look a lot better
after I recruit Chris Tuffley of New Zealand as my secretary.
Chairing the English language committee is a bit like wrestling
crocodiles. The demands of the English language purists are different
from the demands of the people from countries where it is spoken
freely but usually as a second or third language, and both of these
are different from the demands of the foreign-language nations who
wish for a version which is easy to translate.
I observe the law of conservation of commas, removing three from
one question but immediately finding a home for them in another
question.
In the event, a couple of changes will be made later on, causing
much work down the line. I should apologise publicly, either for my
weak performance during the meeting, or for failing to restrain the
enthusiasts later: I don’t know which.
Saturday, 16th July
There is a debate on the marking schemes for problems 1, 2 and
3. The discussion is extremely thorough, and the whole affair does not
lend itself to diarisation.
Sunday, 17th July
The marking schemes for problems 4, 5 and 6 are discussed, and then
the marking scheme to problem 2 is revisited.
The Dutch problem captains have by now perfected an ingenious
strategy: they discuss the marking schemes in such painstaking detail
that the leaders are asleep during the subsequent discussion, and then
Van Duijn wakes them just before the approval vote.
In the afternoon it is time for the opening ceremony: we are bussed
all the way into Amsterdam and taken to a balcony in a large
auditorium. My students are below me; I am permitted to wave and make
the customary thumbs-up sign to them.
The ceremony itself is a fine thing. The speeches are mercifully
short. In the past, the “parade of nations”, where each
team comes onto the stage in turn, has become rather long. This year,
the organisers have decided to break it into groups by continent
(Europe, Asia, the Americas, and Africa/Oceania) with other things in
between, the teams’ movement across the stage is facilitated by
a lithe and acrobatic troupe of performance artists, and the
(thoroughly British) Chemical Brothers’ electronic piece
Galvanize alternates with a folksy Dutch string band playing
variations on the IMO
hymn. I hope that similar improvements become standard.
Afterwards the leaders are removed downtown to the Royal
Netherlands Academy of Arts and Sciences, known as KNAW. There is a
pleasant wine-and-sandwich buffet which prepares us for the drive back
to Eindhoven.
Monday, 18th July
This morning is the first exam for the students, and for the jury
there is a joint meeting with the IMO Advisory Board. Today is a tough
one: we are discussing a proposed reform of the IMO. This is a subject
which inspires much controversy.
The afternoon is a much more lighthearted affair. Four different
excursions have been organised; I have signed up for a bike ride and
mathematical art visit.
Familiarising myself with Dutch bikes is not immediate. The brakes
are activated by backpedalling, and so it turns out to be unwise to
attempt to avoid collision by gripping the handlebars
rhythmically. Also, the rider’s stance is much more upright than
on my bike at home; I deal with this by leaning back as far as I can
and humming the soundtrack to Easy Rider.
The mathematical art visit turns out to be a visit to the house of
the jury secretary Tom Verhoeff’s father Koos. Some forty years
ago, as a mathematician and computer scientist, he was engaged by an
artist to advise on the complicated problems of making closed paths
from straight lengths of beams connected by mitre joins; he eventually
took over the problem and used it as a leitmotif for a life of sculpture.
The family serve us a pleasant tea in small groups, and then Tom
and Koos show us around, explaining the mathematics and design
philosophy that lies behind the artwork.
Back at the ranch, Rozemarijn brings me a couple of post-prandial
cups of tea, and I am happy to exchange gossip. She tells me that
Quintijn Puite is hurtling down a motorway with the scripts. They
arrive slightly earlier than expected.
Our scripts in Problem 1 are pretty strong, and I form an ambition
to receive 42 points for them. My heart sinks when I see UNK2
Carlotti’s script. He has noticed that it is a problem about
integers, and apparently he has some perverse moral code which causes
him to disapprove of this. So he has translated it into an equivalent
problem about rationals. I am surprised and relieved to find that he
then solves it in a sensible fashion, unencumbered by his own
obfuscatory techniques.
It is clear that Problem 2, the Windmill, has been found very hard
indeed. Carlotti has produced a very pleasant solution, of a sort
known to the jury; there is another attempted solution by another
candidate but, heartbreakingly, it contains nothing of value. Several
other students have observed that if you can guarantee to visit points
once, then you can deduce they will be visited infinitely many times:
this should be worth a mark.
We have also made heavy weather of Problem 3. UNK1 Aaronson has
produced a nice script. UNK3 Elliott has a messy attempt which appears
to have some value; nothing else is worth talking about.
Tuesday, 19th July
I pack and check out, then pop in to the Day 2 question-and-answer
session. We are bombarded by nearly 190 questions, mostly asking if
the order of the weights matters in Problem 4. It’s a grave
scene: more than sixty leaders are seen queueing up simultaneously to
answer questions.
After this we are bussed to Amsterdam. I arrive shortly before the
students arrive; we are one big bustling family for lunch.
Five of the students claim Q4; a miscalculation has sent UNK5 Lam
on a wild goose chase, leading to a disappointing day for
him. However, he has many part marks and there is no cause for
embarrassment.
Four of the students claim Q5, and there is no progress at all on
Q6.
After a relaxed late afternoon, the team go bowling while Jack and
I settle down together to read their scripts. Everything is nicely
written, and we feel confident we can get lots of nice points for all
of them.
Wednesday, 20th July
Today is the start of coordination: the process where leaders agree
scores with teams of experts from the host nation.
This seems fated to be smooth. The coordinators have clearly done
their homework well, constructing nuanced and intelligent marking
schemes, and studying the strengths and weaknesses of the scripts
minutely.
In fact, it is so smooth that, when we go in for Problem 1 and one
of the organising crew accidentally delivers us to the correct table
for Problem 2, we can’t find any reason not to coordinate
anyway. After a short battle we get what we ask for, and are then
returned to the intended Problem 1 table. They too give us our 42
marks.
Later on, Problem 4 also does not cause a serious problem; the
students’ work is tidy and little disagreement is possible.
Pleased with a good day’s work, the UK staff retire to the
bar, where I meet a couple of friendly members of the local staff.
Thursday, 21th July
Today is another day of coordination. Quite the most exciting part
of the day is that, as is traditional, we must act as coordinators for
the Dutch team’s scripts on Problem 2, which was a British
proposal (it is felt that having Dutch coordinators deal with the
Dutch team would be insecure). Dion Gijswijt, the capable problem
captain, will be on hand to offer advice.
Jack and I had looked at the scripts (in Dutch, obviously), but had
made no preparation for tackling Johan and Sietske. But, in the event,
we fall naturally into a good cop/bad cop routine. I humour them into
thinking a mark is appropriate, and then Jack tells them it
isn’t worth one. In the end they get a 6 for a very pleasant
solution, and a 1.
Then we return to our own problems, in the most literal of
senses.
Problem 3 is quite involved. Ben Elliott’s script, which
should be worth two marks, is a mess: the good stuff is buried in
among a bit of bad, and the coordinators have gone off the rails
thanks to misreading some dodgy handwriting. Jack explains the script
carefully, and we are sent away so they can think about it in
peace. We are ushered back a few minutes later: they agree, and we
pick up the points.
Problem 6 is an easy coordination. We ask boldly for six zeroes,
and the coordinators give way and agree immediately.
Lastly we coordinate Problem 5. Four 7s and a 2 for UNK6 Millar are
uncontroversial. We observe that a score of 4 for Lam is an immediate
consequence of the marking scheme. This point appears to be recondite,
but eventually we get the 4.
Jack then disappears for a post-coordination snooze, and I loiter
in the lobby to pick up gossip and rumours about our relative
performance. Things seem all right.
Friday, 22th July
The morning begins with the final jury meeting. This one is
theatre, and deputies and observers are invited. The first part of the
business consists of hearing reports from the chief invigilator and
chief coordinator.
The former report is studded with statistics: it’s good to
know that the organisers were paying close attention. Next year I
expect to be told the maximum variation in desk thickness, and the
standard deviation in the times elapsed before the first toilet visit
by each team.
Then comes the choice of medal boundaries. The organisers’
proposal is a nice surprise for us: it gets Andrew his gold. Adam will
feel bad about not being able to scrape together another mark for a
silver, but I’m sure he’ll be in fighting condition for
next year’s IMO. All other medals were as suspected.
After this is an excursion to central Amsterdam. Our guide Vicky
wishes to take us walking around the parks; Geoff chooses a less
ambulatory option and sits in a cafe for an hour and a half. Then we
pick him up for a canal boat trip, which does a good job of explaining
the history of Amsterdam; Messrs. Aaronson, Carlotti, Elliott, and
Shotton sleep through a large chunk of it.
From there we walk to the Dam, the large square in the centre of
the city. Vicky expertly avoids the red light district to take us to
the science museum NEMO, where there is a hot buffet dinner and a
party.
It turns out that having a party in a science museum is a very good
idea.
There is a rock band, comprising the motlier parts of the IMO
staff. They finish up with the timeless Metallica classic Enter
Sandman, and I feel the urge to go and jump up and down with the
students. Jordan and Josh walk in, and Jack greets them, “James
is on the dancefloor. He’s a complete metalhead!” They
spend a while looking disbelievingly for James Aaronson before coming
to their senses.
Afterwards I notice I have become warm and go sit outside, enjoying
a commanding twilight view of Amsterdam.
Saturday, 23th July
In the morning there is another meeting: a joint jury meeting with
the IMO Advisory Board. This is to finish discussion of IMO reform. It
is clear that the majority mood is currently against any radical
change, but there is a vote to create an “ethics
committee”. This will be the IMO police, with the job of
investigating any suggestions of dodgy behaviour at the IMO.
The other, much more pleasant, piece of business is to accept
proposals from the Advisory Board on future IMO hosts. We had long
since been planning IMO 2012 in Argentina, but had not had any more
hosts lined up. However, this year we agree on three more: IMO 2013 in
Colombia, IMO 2014 in South Africa, and IMO 2015 in Thailand.
The meeting gives way to lunch, and a little later we walk to the
closing ceremony.
The closing ceremony does not suffer from the disadvantages of
overpreparation. The compère, apparently a Dutch televisual
national treasure from the same mould as Valerie Singleton, confirms
common suspicion by announcing at one point that she has no idea what
she is doing. Nevertheless, the students do: the medals are all
awarded, and apparently all to the correct people.
The closing ceremony gives way to the afterparty next door. The
most important piece of business here is the multilingual presentation
of the Golden Microphone, for the leader who has given the most
speeches in the jury meetings. This year it is won by the Brazilian
leader: an amazingly loquacious performance. I was told that I was
third; I consider this not bad for a first attempt.
Despite the rain, the atmosphere is rather good. Jack and I are
even persuaded to dance; our failings are carefully insulated from the
students by a barrier of guides and organisers.
Sunday, 24th July
I am woken up early by Adam Goucher’s knocking upon my
door. He tells me to get up in −5 minutes. It seems I mis-set my
alarm clock: it is lucky that my students are less incompetent.
We must get to Schiphol for a morning flight, but there is time for
two final presentations.
The first is my jury voting stick, the Sceptre of Unk, a
device with mystical powers including (but not limited to) preventing
its wielder from making false statements. I give this to Josh, so that
he may use it for the next eleven months and two weeks.
There is also the Golden Pen donated by the students: this
is given to the student with the nastiest script that ends up
obtaining seven marks. Rewarding such people with extra writing
implements seems like playing with fire, but I am nonetheless pleased
to bestow it upon Ben.
Our final farewells and the repatriation of team UNK, by a short
flight to Gatwick, are uneventful.
Thanks
For a nation to successfully participate in the IMO requires vast
effort, and the staff actually present at an IMO are at best the tip
of the iceberg.
Except for a skeleton staff in Leeds, all the olympiad work in the
UK is entirely voluntary, and many of our volunteers are stoically
insensitive to the damage caused to their careers, studies and
relationships by the heavy expenditure of time.
I would like to mention many of the people and groups to whom I owe
thanks:
- James, Andrew, Ben, Adam, Josh and Jordan, for making me proud;
- Jack, for being an excellent deputy and a good friend;
- Vicky Simon-Akerboom, our wonderful guide;
- Sally Anne, for being there for the students;
- Joseph Myers and Sean Moss, for helping run a pleasant and
informative pre-IMO camp;
- Paul Russell, Tim Gowers and Bryn Garrod, for getting our students
excited by mathematics at a crucial time;
- Bev Detoeuf and Rachel Greenhalgh, for their solid logistical work
in the UKMT office;
- Richard Freeland and Ed Kirkby, for raising the standards of the
training from within;
- My predecessors Tony Gardiner, Adam McBride and Imre Leader, for
providing invaluable advice on what constitutes good education;
- The students’ families and schools, for putting up with the
disruption of a serious IMO campaign;
- All the mathematicians and UKMT volunteers who have helped train
the students over the course of the year;
- The IMO organisation and students of Australia and Hungary for
showing warmth and good mathematics to our students;
- Tom Lovering, (Luke) Alexander Betts, and the international
problem submissions group for managing that side of the British IMO
effort;
- All the other leaders for making me, a rank novice, feel welcome
among them: I’m particularly grateful for the wisdom and
experience of Zuming Feng, Indra Haraksingh, József
Pelikán and Paul Vaderlind;
- Geoff Smith MBE, for constant energetic support, advice and help
of all sorts throughout the year;
- Most pointedly, the staff of IMO 2011: they did a fantastic
job. We were particularly impressed by Rozemarijn Schalkx, Ronald van
Luijk, Tom Verhoeff, Birgit van Dalen, Matjaž Željko, Wim
Berkelmans, Quintijn Puite, and Hans van Duijn. However, the friendly
and personable nature of the senior organisers can serve to mislead,
by hiding the vast amount of work done by a multitude of largely
invisible guides, IT specialists, journalists and crew members.
James Cranch (jdc41@cam.ac.uk), 27th July 2011.
Return to IMO Register home page
Contact: Joseph Myers
(imo-register@imo-register.org.uk)
Online HTML version last updated:
5 January 2016
![]() be a finite set of at least two points in the plane. Assume that
no three points of
be a finite set of at least two points in the plane. Assume that
no three points of ![]() are collinear. A
windmill is a process that starts with a line
ℓ going through a single point
are collinear. A
windmill is a process that starts with a line
ℓ going through a single point ![]() . The
line rotates clockwise about the pivot P
until the first time that the line meets some other point
belonging to
. The
line rotates clockwise about the pivot P
until the first time that the line meets some other point
belonging to ![]() . This point, Q,
takes over as the new pivot, and the line now rotates clockwise
about Q, until it next meets a point of
. This point, Q,
takes over as the new pivot, and the line now rotates clockwise
about Q, until it next meets a point of
![]() . This process continues indefinitely.
. This process continues indefinitely.![]() and a line ℓ going through
P such that the resulting windmill uses each point
of
and a line ℓ going through
P such that the resulting windmill uses each point
of ![]() as a pivot infinitely many times.
as a pivot infinitely many times.