International Mathematical Olympiad 2013
UK leader’s report: GCS
August 2013
The 54th International Mathematical Olympiad was held on the
Caribbean coast of Colombia in July 2013. The students stayed in Santa
Marta, and the leaders in Barranquilla, at the mouth of the Rio
Magdalena. The UK Team Leader was Dr Geoff Smith of the University of
Bath and the Deputy Leader was Dominic Yeo of Worcester College,
Oxford. The person in charge of pastoral matters is our Observer C,
Bev Detoeuf from the Leeds Office of UKMT.
The team was as follows:
| Andrew Carlotti | Sir Roger Manwood’s School, Kent |
| Gabriel Gendler | Queen Elizabeth’s School, London |
| Daniel Hu | City of London School |
| Sahl Khan | St Paul’s School, London |
| Warren Li | Fulford School, York |
| Matei Mandache | Loughborough Grammar School |
The reserves were
| Frank Han | Dulwich College, London |
| Maria Holdcroft | Willink School, Berkshire |
| Freddie Illingworth | Magdalen College School, Oxford |
Andrew Carlotti was competing for the fourth time, and by securing
a gold medal at IMO 2013, he now has the best IMO medal record of any
British student. He has one bronze medal and three gold medals, won
during 2010–13. This takes him above Simon Norton (3 gold
medals, 2 special prizes) and the late John Rickard (3 gold medals, 3
special prizes).
The performance of the British team of 2013 is shown in the
following table:
| | P1 | P2 | P3 | P4 | P5 | P6 | Σ | Medal |
|---|
| UNK1 | Andrew Carlotti | 7 | 7 | 0 | 7 | 7 | 6 | 34 | Gold |
| UNK2 | Gabriel Gendler | 7 | 5 | 0 | 7 | 6 | 0 | 25 | Silver |
| UNK3 | Daniel Hu | 7 | 7 | 0 | 7 | 7 | 2 | 30 | Silver |
| UNK4 | Sahl Khan | 7 | 0 | 0 | 7 | 7 | 0 | 21 | Bronze |
| UNK5 | Warren Li | 7 | 7 | 0 | 7 | 7 | 0 | 28 | Silver |
| UNK6 | Matei Mandache | 7 | 7 | 0 | 7 | 7 | 5 | 33 | Gold |
The cut-offs were 15 for bronze, 24 for silver and 31 for gold.
There were 97 participating nations. The unofficial ranking of
countries by total scores has the UK in 9th position overall, 2nd
among European nations (behind Russia), and in 1st position among the
nations of the European Union (by some margin). This represents the
best team performance by a British side at an IMO since 1996 when we
finished 5th.
Here are the top 30 places at IMO 2013. The full table can be found
at
http://www.imo-official.org/year_country_r.aspx?year=2013
1. China (208), 2. South Korea (204), 3. USA (190), 4. Russia (187),
5. North Korea (184),
6. Singapore (182), 7. Vietnam (180), 8. Taiwan (176)
9. United Kingdom (171),
10. Iran (168),
11. Canada (163),
11. Japan (163),
13. Israel (161),
13. Thailand (161),
15. Australia (148),
16. Ukraine (146),
17. Mexico (139),
17. Turkey (139),
19. Indonesia (138),
20. Italy (137),
21. France (136),
22. Belarus (134),
22. Hungary (134),
22. Romania (134),
25. Netherlands (133),
26. Peru (132),
27. Germany (127),
28. Brazil (124),
29. India (122),
30. Croatia (119).
Of the remaining nations, Anglophone and Commonwealth scores
include 31. Hong
Kong (117), 31. Malaysia (117), 48. New Zealand (77),
56. Sri Lanka (65), 58. South Africa (64), 61. Bangladesh (60),
64. Cyprus (52), 76. Ireland (33), 79. Pakistan (25),
84. Nigeria (18), 86. Trinidad and Tobago (16), 95. Uganda (1).
Italy are to be congratulated for finishing top of the nations
using the Euro. France finished above Germany, a singular event
which had not happened since German re-unification. There seems to be
a general trend that some of the countries of central and eastern
Europe are getting lower IMO rankings, whereas the nations of the Far
East are doing very well recently. Indonesia obtained an excellent
result, a sharp improvement on their previous performances, and Israel
secured their best ranking position since 2000. As often happens,
China sent a very strong team, and are to be congratulated for winning
the event.
Problems of Day 1
-
Prove that for any pair of positive integers k
and n, there exist k positive
integers m1, m2, …,
mk (not necessarily different) such that
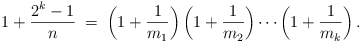
-
A configuration of 4027 points in the plane is called
Colombian if it consists of 2013 red points and 2014 blue
points, and no three of the points of the configuration are
collinear. By drawing some lines, the plane is divided into
several regions. An arrangement of lines is good for a
Colombian configuration if the following two conditions are
satisfied:
- no line passes through any point of the configuration;
- no region contains points of both colours.
Find the least value of k such that for any
Colombian configuration of 4027 points, there is a good
arrangement of k lines.
-
Let the excircle of triangle ABC opposite the
vertex A be tangent to the side BC
at the point A1. Define the points
B1 on CA and C1 on
AB analogously, using the excircles opposite
B and C, respectively. Suppose that
the circumcentre of triangle A1B1C1 lies on the
circumcircle of triangle ABC. Prove that triangle
ABC is right-angled.
The excircle of triangle ABC opposite
the vertex A is the circle that is tangent to the
line segment BC, to the ray AB
beyond B, and to the ray AC beyond
C. The excircles opposite B and
C are similarly defined.
Problems of Day 2
-
Let ABC be an acute-angled triangle with
orthocentre H, and let W be a point
on the side BC, lying strictly between
B and C. The points M
and N are the feet of the altitudes from
B and C, respectively. Denote by
ω1 the circumcircle
of BWN, and let X be the point
on ω1 such that WX is a
diameter of ω1. Analogously, denote by
ω2 the circumcircle
of CWM, and let Y be the point
on ω2 such that WY is a
diameter of ω2. Prove that X,
Y and H are collinear.
-
Let ℚ>0 be the set of positive
rational numbers. Let
f:ℚ>0 → ℝ be a
function satisfying the following three conditions:
- for all x,
y ∈ ℚ>0, we have
f(x)f(y) ≥ f(xy);
- for all x,
y ∈ ℚ>0, we have
f(x + y) ≥ f(x) + f(y);
- there exists a rational number
a > 1 such that
f(a) = a.
Prove that f(x) = x for all
x ∈ ℚ>0.
-
Let n ≥ 3 be an integer, and
consider a circle with n+1 equally spaced points
marked on it. Consider all labellings of these points with the
numbers 0, 1, …,
n such that each label is used exactly once; two
such labellings are considered to be the same if one can be
obtained from the other by a rotation of the circle. A labelling
is called beautiful if, for any four labels
a < b < c < d
with a + d = b + c,
the chord joining the points labelled a and
d does not intersect the chord joining the points
labelled b and c.
Let M be the number of beautiful labellings, and
let N be the number of ordered pairs
(x,y) of positive integers such that
x + y ≤ n and
gcd(x,y) = 1. Prove that
M = N + 1.
Diary
The Director of IMO 2013 was Maria Losada (not be confused with
Maria Falk de Losada, her mother and the chair of the jury). Maria
Losada was immensely helpful to the Australian and UK teams,
facilitating our early arrival, monitoring our hotel bookings, and
inviting the UK team guide Maria Ximena Rueda to join us for our
pre-IMO camp. Maria Losada does not play a large role in this diary,
but she orchestrated the IMO, and without her work, and that of her
team, the IMO could not have happened.
Sunday July 14th
We have an early flight tomorrow, so some of us gather at a
Holiday Inn near Heathrow Airport. This involves meeting the
flight of Daniel and Matei, silver medallists from the International
Physics Olympiad in Denmark. They are having to miss the physics
closing ceremony to join us for the journey to Colombia. Our
International Olympiad in Informatics (Computing) silver medallist,
Andrew Carlotti, will be making his way from the IOI in Brisbane in
the company of the Australian IMO team. They have to travel via New
Zealand and Chile, and Andrew should arrive in Santa Marta a few hours
before we do.
Monday July 15th
We have ordered a giant taxi, but a merely large one arrives. We
quickly arrange for a more impressive vehicle, and make our way to
Terminal 5. We find Sahl there, so the party is as ready as it
is going to get until we reach Colombia.
We are delighted to discover that our Iberia/Avianca flights will
take our checked-in luggage all the way to Santa Marta. The first hop
to Madrid goes easily enough. In Madrid we have to change terminals,
and we do so in the hope that our luggage will move as swiftly.
The long journey to Bogota involves trays of baby-food, mysterious
pastes which were presumably obtained as surplus goods from NASA. I
am the happy position of being moved to a row of seats with no other
passengers. Ten hours later, or just four hours later if you are
foolish enough to use local time, we find ourselves in Bogota. We are
at a great altitude, so the conditions are not oppressive.
The students are hungry, and we quickly locate a traditional
Colombian Japanese sushi and sashimi restaurant. The
students spot a flight information board, and Gabriel convinces us
that our flight to Santa Marta has been cancelled. I compound the
error by taking him seriously. Eventually it turns out that we have
been looking at the arrivals board.
The correct departure gate is unmarked, but by determined
negotiation we eventually find ourselves waiting in the right
place. At last there are a few maths T-shirts around, and it is clear
that we are getting close to the IMO. Our Colombian guide Maria
introduces herself, for she has kindly agreed to act as translator
during the Australia-UK pre-IMO camp.
The flight to Santa Marta is in the dark, and when we arrive, we
step off the aircraft into proper tropical air that you can chew. Our
bags soon arrive, and we locate the minivan which has been sent to
meet us from the Santorini Hotel. It has been a long day, and
while people are not yet irritable, the bonhomie is getting a
bit forced. The chap in charge of loading the bags is of a certain
age, and rather ponderous. Eventually we intervene and load the bags
ourselves. We are then crammed into the van for the short journey to
our hotel.
I can tell that we have arrived when I see the Australian leaders
Angelo di Pasquale and Ivan Guo standing by the side of the road.
There are various conflicting instructions as to what we should do
with (a) our bags and (b) ourselves. Eventually we get out and Bev
does battle with a UKMT credit card and the very confused check-in
staff. After over half an hour (I kid you not) she succeeds in making
the appropriate credit card payment, and leads the students off to the
UK villa.
Then Dominic and I stroll up to the counter to collect our room
keys, and are astonished when the staff explain that Bev has not paid
for us, and we must pay before we are given our keys. We are
exhausted, and not in the mood for a fight, so I pay using my UKMT
credit card and we get our keys.
Dominic shoots down to the UK villa. He and Bev study our
paperwork, and we discover that Bev had indeed paid for us. Dominic
comes back to my room, takes my credit card, and gets the second
payment reversed by the gentlemen in reception. Dominic is initially
of the opinion that the receptionists are crooks, but having seen
earlier events, I reassure him that they are just massively
incompetent.
I am now drained after this prodigious journey, and am not best
pleased when the clowns in the room next door decide to have loud
conversations on their balcony until past 4am. As I drift off to
sleep, someone sets off firecrackers to entertain the hotel at
5am. Things can only get better.
Tuesday July 16th
The Australian and UK students each have their own villas, and we
rearrange the social spaces to create exam rooms, borrowing furniture
from the nearby pool area when necessary. While they sit the paper, I
go to reception, and have my room changed to get away from the selfish
idiots who were in room 511 last night.
We get bread, cold meats, cheese and tropical fruit drinks from a
local supermarket, and have an improvised lunch when the exam is
over.
The British students have bested the Australians on the first
paper, but only by a narrow margin. I am impressed, because I know
that the British side is very good. It seems that the Australians will
not be a pushover this year, and that our continued possession of the
Mathematics Ashes is in doubt. The contest is the final exam of
the pre-IMO camp.
Wednesday July 17th
After my first good night’s sleep in Colombia, I am to be
picked up by a minivan taxi for the transfer to the city of
Barranquilla while the students are sitting an exam. Checking out
involves tangling once more with the characters in reception. To
simplify matters, I take along an itemized list of my extras, so that
settling up should be a straightforward process. They wave my list
away, and start tapping at computer terminals. After the usual 30
minutes, they come up with a completely incorrect figure. I point out
that they have failed to allow for the items associated with my second
room. There is much slapping of palms on foreheads, and they decide
simply to let me off those items, presumably because my taxi is due
and it would take another 30 minutes to add two numbers together.
Mike Clapper of the Australian Maths Trust, together with his
partner Jo, arrive from the airport just before my taxi turns up, and
we exchange warm greetings. Their luggage has vanished somewhere
between Brisbane and Santa Marta, but they seem happy enough just to
have arrived.
My taxi parks outside, and I bid farewell. The van is cool and
quick, and we drive to Barranquilla in under 2 hours. For much of the
journey, the sea is on your right, and a large lake is on your left,
and as your mind drifts, it is not clear which is which. It feels like
you are travelling on a tropical Afsluitdijk, with pelicans and
countless white herons for decoration. I am travelling with several
other team leaders: Dieter Gronau from Germany, Raphael Steiner from
Switzerland, Philipp Wirth from Liechtenstein and Bernd Kreussler from
Ireland.
It is a curious feature of Colombian geography that it has cities
and towns, but the villages are mostly missing. There is one small
settlement in the middle of the journey, and there we could see the
sharp disparities of wealth which bedevil Colombia and many other
Ibero-American societies.
At length we arrive at the El Prado hotel in Barranquilla. This is
not an ordinary modern hotel, but rather it dates from the 1930s, and
is fit for Ernest Hemingway. The reception staff act as if they have
never heard of the IMO, and give us room keys and the information that
we will get free breakfast tomorrow. Since today’s lunch is now
overdue, this is disconcerting. I leave my luggage in my room, and
conduct a random walk through the hotel. Eventually I spot IMO
internet Tsar Matjaž Željko, and tail him until he leads me
to the IMO office. I get the shortlist, and tokens that can be
exchanged for meals.
Thursday July 18th
I enter an email exchange with my brother Pete, who lives in Dubai.
After a couple of decades of making things happen, he has recently
written a book (Project Management: All You Need is Love) and is
developing a literary bent. He sets himself the challenge of getting
the British and Australian press interested in the Mathematics Ashes,
and over the next few days he works on a blog with this purpose. We
swap ideas during my night and his day, but the text is all his.
http://otherashes.wordpress.com/2013/07/19/and-so-it-begins/
The Mathematics Ashes has its origins in a hotel bar in IMO
Vietnam, where, after several beers, the former Australian Mathematics
Trust supremo Peter Taylor suggested this annual competition, and
Peter Taylor is very much in on the gag. Joseph Myers keeps the
Mathematics Ashes records in a more formal style.
http://www.bmoc.maths.org/home/ashes.shtml
Friday July 19th
The jury has its first serious meeting. In my Observations of 2011
(http://www.imo-register.org.uk/2011-report-geoff.pdf)
I made a “modest proposal” to reform IMO voting protocols,
and the case for change was made more pressing by the unbalanced
papers of 2012. The new protocol involves forcing problems 1, 2, 4 and
5 to involve all four subject areas, and then choosing the best two
hard problems on merit alone, unconstrained by subject type except
that they should not be from the same area as one another.
The mechanism for producing the balance in the easy and medium
problems is to choose eight problems. For each of the areas algebra,
combinatorics, geometry and number theory the jury can choose the best
easy and the best medium problem. The easy and medium positions can
then be filled in 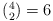 ways. The
jury pauses for reflection on the relative merits of the six choices,
and then votes off possibilities one at a time. The idea is that each
problem that appears on the paper must be the best available question
in its category, and that the easy/medium problems, the ones which
most students actually try to do, will be balanced.
ways. The
jury pauses for reflection on the relative merits of the six choices,
and then votes off possibilities one at a time. The idea is that each
problem that appears on the paper must be the best available question
in its category, and that the easy/medium problems, the ones which
most students actually try to do, will be balanced.
There is an extended debate, and eventually the jury agrees to try
the new protocol for one year as an experiment. Whether the new method
is adopted again is a matter for future juries, and I suppose that
will partly depend on how people judge the quality of the 2013 paper.
Anyway, having lit the touchpaper, I sit back and wait for
disaster.
The jury chair is Maria Falk de Losada, a formidable Colombian New
Yorker who eats fools for breakfast. She wants us to discuss the
merits of the problems. This is an excellent idea, but it is too
soon. It turns out that many leaders (me included) want to be left
alone to struggle with the shortlist problems in their rooms, and we
persuade the chair to give us more time.
Saturday July 20th
At length we have the solutions to the shortlist problems, and we
can start to make rational judgements about the merits of the of the
harder problems. We implement the new protocol, and a paper is
produced. One well-known jury figure is convinced that the paper is
too easy, and that we have really messed it up this year. I am not so
sure. We have chosen a purely conceptual problem in position 2, and
our experience with the 2011 windmill was that many students find such
questions very difficult.
Viewing the internet late in the evening, I discover that the UK
has retained the Mathematical Ashes by 1 point. The Australians set an
easy Ashes paper to compress the marks.
Sunday July 21th
Today is student arrival day in Santa Marta, but this is of little
import at the jury site. The jury begins the day by working on the
notation that will be used in the problems. Having established that,
the English Language Committee kicks into life, with its open door
entry qualification. Chris Tuffley of New Zealand constructs the
computer file, and after our deliberations we make our proposal to the
jury, and after further discussion we have the English language
versions of the papers. A few hours later we approve the other IMO
official languages, and finally the leaders go to work to produce the
papers in all necessary languages.
Monday July 22nd
The jury approves the final versions of the papers, and then we
travel to the opening ceremony. This is held in a very large
university hall. There are short and welcome speeches from various
members of the Losada family, and a political address from the mayor
of Barranquilla which set everyone thinking.
We then entered the important phase of the ceremony, when the teams
paraded one by one round the arena, accompanied by various grotesque
figures from the Colombian carnival. The conception was brilliant.
This bizarre procession was accompanied by carnival music: horns,
drums and accordions. No review that I might give would do it
justice.
The UK team members, dapper in shirts, ties and panama hats, take
their turn. Sahl is carried round by Gabriel, while Andrew, Daniel,
Matei and Warren stroll round while waving.
At the end of the ceremony, the leaders depart for Cartagena, a
beautiful old Spanish port along the coast. The architecture is
beautiful, and we have a happy time wandering around the town. The
city walls are intact, put there to protect Cartagena from English
pirates. On the way back to our hotel, the driver gets lost in
Barranquilla. This is no mean feat because the roads are set out and
numbered on a grid system, American style. I wonder if he is related
to the people working at reception in the Hotel Santorini?
Tuesday July 23rd
Checking the internet in the morning, I discover that the baby who
will become Prince George of Cambridge has been born. This is a
disaster for my brother Pete’s plan to get publicity for the
Mathematics Ashes. The journalists who planned to give name checks to
the team members in the British press have had their stories spiked.
Their editors have given over space to the “woman gives birth to
baby” story. As Pete put it, we were “bumped by the
bump”.
It is the morning of the first exam, and the jury convenes to
answer questions of clarification from the students. There are one or
two technical problems, one of which is resolved by turning a
television screen upside down.
The co-ordinators present their marking schemes. Initially there
are no paper copies, and that makes it very hard to view the schemes
in the round. This is sorted out fairly quickly.
In the evening we attend the mayor’s reception, and listen to
more of that carnival music. The most impressive aspect of the event
was the extraordinarily powerful amplification system. You can
imagine how much we enjoyed that.
On returning to the hotel, we find that the students scripts are
expected to arrive at about 11pm. I go to bed rather than wait.
Wednesday July 24th
I pick up the UK scripts before breakfast. My initial reaction is
that the jury has messed up very badly, and problems 1 and 2 must be
far too easy, because the British students have demolished them. I
prepare for the worst. No doubt the new voting protocol will be
blamed, and I will lose all respect from my fellow jurors.
I ask other leaders how their students have done, and to my
surprise it seems that many students have found problems 1 and 2 quite
difficult. While I am sorry for the students personally, it is a
relief that the paper has not been completely misjudged. The British
students have done unusually well on paper 1. It is a shame that there
is so little work on problem 3, not even many good diagrams.
We have a much more efficient Q & A session for the first 30
minutes of paper 2, and then listen to the well-presented marking
schemes for the problems of day 2. We have lunch and then transfer to
the students’ site. There has been little time to work on the
scripts of day 1. This is not a problem for me, because the British
solutions fall easily into two categories: completely right or total
rubbish. Many leaders will have more subtle issues to resolve, and I
feel for them.
The students’ site, the Irotama Resort, is a wonder to
behold. It is a huge resort complex set right on the beach. Many
people are housed in beach bungalows, but I am in a tall apartment
block. In my suite we have our own bedrooms, but I share a common
social area with Dieter Gronau of Germany and Gregor Dolinar of
Slovenia. The apartment is well equipped, with a chilled water
dispenser and a washing machine.
It is delightful to meet the UK team, and both Bev and Dominic.
Everyone is well, and the students are claiming to have done better on
day 2 than day 1. If this is true, we are going to have our best performance
for years. I ask other leaders, and while problem 4 is widely regarded
as accessible, problem 5 is viewed as quite challenging and problem 6
as very hard indeed.
In particular, Andrew Carlotti is an extremely happy bunny, and he looks
almost certain to pick up his third gold medal. It also seems certain
that all our team will get medals, and that many of them will be strong.
We leave Bev to keep an eye on the team, and Dominic and I go into
mark maximization mode. It is really only problems 3 and 6 where we
are likely to have complicated co-ordinations. Dominic takes the combinatorial
problem 6 and this leaves me with the geometric problem 3.
It is a long evening, but not as long as it might have been.
Thursday July 25th
On the first day of co-ordination we address problems 1, 5 and 4.
The marks harvest is 125/126, but we know that day 2 will be a
more testing experience.
The co-ordinators seem well prepared, and the co-ordination room is so well
air-conditioned that there is an incentive to prolong discussion
indefinitely.
There are now ample opportunities to meet old friends among the
deputies and observers, and of course to strike up new relationships.
Friday July 26th
Our first co-ordination in on problem 3. One of our co-ordinators
is Mark Saul, whom I have known for a long time. I lead.
There are only two scripts of interest. Daniel Hu has not done
the problem, but he has done the converse (that it is, he has
proved the reverse of what is required). The marking scheme
helpfully and explicitly states that there are no marks available
for doing this, but I begin by asking if case law has developed allowing
partial credit. It has not, and we move on.
Next we examine Andrew Carlotti’s script. This is all rough work,
but he has circled a piece of work on page 9 which is interesting.
It is written in his characteristic stream of consciousness style,
but if carefully read, it is an outline of part of the
necessary proof, a part which is worth 3 marks.
I have seen co-ordinators give full marks for material like this,
and I have also seen them give zero. The extreme perspectives are
(i) “this is an essentially correct solution, but the student has
written it up (probably under time pressure) very casually,
but we are here to reward ideas, not neat and accurate presentation,
so we allow this as a proof” and
(ii) “you have supplied a very interesting way to interpret these
jottings, and we commend your ingenuity, but we are here to
mark the student’s script, not the quality of your interpretation”.
Unfortunately the co-ordinators are firmly of the latter view, and though
we obtain a second opinion from Jana Madjarova of Sweden, we cannot squeeze
out a mark.
Dominic is to lead on the remaining two questions. Problem 2 is
the geometric combinatorics problem proposed by Ivan Guo of Australia.
We have four clear solutions, one clear non-solution, and an incomplete
solution by Gabriel Gendler, written up against the clock. Dominic forecasts
5 points for Gabriel in advance, and that is exactly what we get, along with
four 7s and a 0.
Finally we move to problem 6. After day 1, no student of any country
had obtained a mark for
this problem on the public display. We have three scripts with
content. Andrew Carlotti gets 6, Matei Mandache gets 5 and Daniel Hu gets
2. This is roughly in line with Dominic’s forecast, though he has to do some
very hard work to convince the co-ordinators of our case. Dominic’s
mastery of his brief is excellent,
and tries very hard to persuade the co-ordinators that Daniel’s script
is worth more than 2, but they will not budge. Since the gold medal
cut-off seems likely to be about Daniel’s score, this could be very important.
In the evening we had the joint IMOAB and jury meeting.
We begin by remembering those who have, in the language
of Erdős, “left”. This includes my friend and
co-author Christopher
Bradley, and I give a short summary of his contributions and career.
The jury stands in respect.
There is an announcement about the film, being made in the UK at the
moment, provisionally entitled X PLUS
Y. This is a love story, the main players being
two young people from different IMO teams. The IMO Foundation should
be in a position to make use of the publicity to try to garner support
for the IMO, and for this reason it is being reconfigured.
The runners and riders for the IMOAB elections are announced, nominations
having been gathered at IMO 2013. There are many candidates for the
positions on the IMOAB, but only two candidates for the IMOAB
chair. I happen to know that each of these two candidates nominated
the other, so we can expect the usual extremely amicable election
at IMO 2014.
Finally we study the mark distribution at IMO 2013, and decide upon
the medal cut-offs: 15 for bronze, 24 for silver and 31 for gold.
Saturday July 27th
There is a tourism opportunity in the morning, but all
the UK participants take a rest. At 3pm we have a brief
meeting of countries interested in EGMO (the European
Girls’ Mathematical Olympiad). The event will be held
next year during April 10–16 in Antalya, Turkey, but
thus far we have no host country for EGMO 2015.
In the afternoon we visit the
Santa Marta botanical gardens, adjacent to the house where
Simon Bolivar died in 1830. We are gathering for the medal ceremony.
At this moment I am approached by the leaders of Belarus,
Igor Voronovich and Sergei Mazanik. They have just received a
message from the Belarus Ministry of Education that they are
prepared to support an edition of EGMO. We pencil in Belarus as
hosts of EGMO 2015. I am very excited about this excellent news.
There is a brief ceremony involving some ornately dressed soldiers,
and IMO chair Nazar Agakhanov lays a memorial wreath. After that we
have an outdoor medal ceremony, and finally return to the Irotama
hotel for the farewell dinner round the pool (which was brilliantly
planned) and the presentation of the Microphone d’Or. The
competition for the most garrulous juror is organized by Rafael
Sánchez of Venezuela. Rafael has asked me to make the speech,
so I prepare some offensive remarks. Unfortunately Angelo is busy
trying to check-in the Australian team for the flights home. We find
his deputy, Ivan Guo, and he kindly agrees to substitute for his
leader.
The usual characters crowd on stage for the ceremony, and
speeches are translated into all official languages. Ivan
accepts the golden microphone with a few well chosen insulting
phrases about his leader, and honour is satisfied. Angelo beat
me by one speech!
Sunday July 28th
I wake up and check my email. There is a worrying
message from Adam McBride that David Monk is
in intensive care with heart problems. David has
been a stalwart of UK IMO preparation since the
1960s, and he is known and loved internationally
because of his beautiful problems. He is the most
prolific author of IMO problems, having created
no less than 13 over the years (he is sometimes given half a credit
for another problem, but he repudiates this). He wrote the wonderful
“New Problems in Euclidean Geometry” a few years ago
(published by UKMT).
At breakfast I share this disturbing news with other leaders
and it gives us all pause for thought. (As I write this report,
the good news is that David is recovering well, and
has just been allowed home.)
Indra Haraksingh from Trinidad and Tobago kindly tries to give
me a T-shirt. I am flattered by the 2XL size label, but explain
that this is not realistic.
I look for the UK guide Maria and am disappointed to
discover that she has already left
for Bogota. Good luck to her at MIT.
The UK team catches the 10:30 am bus and arrives in good time at
Santa Marta’s Simon Bolivar Airport. We meet a Uruguayan
contestant who is desperate for a hamburger. Presumably this is a form
of homesickness. The airport, and subsequently our plane, fills up
with IMO teams.
At Bogota we have little time to change planes, but the team are
hungry so they demolish a quick meal. I go on ahead, and hear repeated
calls for “Carlotti” over the tannoy. The whole team turns
up oblivious to team member Andrew’s new-found celebrity. My
best guess is that he has dropped his passport in the loo, but no. It
turns out that the Colombian customs authorities want to inspect his
checked-in luggage. Bev and Andrew hurtle off to do the
necessary. Fortunately they arrive back quickly, and we board as
normal.
This time Bev has managed to persuade the airline not to ignore our
food requirements, and people get the meals they want. This is an
overnight flight, so we hope to sleep. I am initially disappointed to
be trapped by an aisle seat passenger, but after inspecting her new
neighbour, she magically disappears. It is a gift I have.
This means that I can spread sideways, leaving more space for my
colleague Dominic. This is all very satisfactory. I insert earplugs
which nearly, but not completely, cut out the loud conversation from
the wretches behind who decide to flirt at volume while the rest of
the plane is trying to sleep. Don’t you just love attractive
young people?
Saturday July 29th
We arrive in Madrid a little after 9am local time. We have ample
time to change planes and terminals and have a meal. We take a
lunchtime flight to London. This turns out to be more exciting than we
had planned. Just as we are about to touch down, the landing is
aborted and the plane’s engines scream at full power as we climb
away at speed. When we are at a safe height, the captain explains
that air traffic control called off the landing because the previous
plane had failed to clear the runway in time. I looked up the
statistics on this when I arrived home. It happens to about 1 landing
in 400 at Heathrow.
The luggage comes through the excellent Terminal 5 system of belts
and tubes in no time at all, and we go outside to be met by happy
families. We distribute medal and participation certificates, and it
is over for another year.
Thanks
Thanks to everyone who made this possible. Thanks to the the
families and the Leeds Office of UKMT, and the small army of UKMT
coaches and mentors and the organizers in Colombia. Thanks to James
Cranch for having played such a key part in training over the past
couple of years, and to my colleagues Dominic and Bev for countless
kindnesses.
Finally I thank the students. Their behaviour was excellent
throughout. They clearly enjoyed one another’s company, and
maintained an unceasing interest in working on mathematics problems
before, during and after the IMO. Two are available for IMO 2014, and
as for the other four, I give the University of Cambridge fair warning
of what is coming.
Return to IMO Register home page
Contact: Joseph Myers
(imo-register@imo-register.org.uk)
Online HTML version last updated:
5 January 2016
![]()