UK IMO team leader’s report
Geoff Smith, University of Bath
August 2015
This year the International Mathematical Olympiad
was held in Chiang Mai, Thailand.
The IMO is the world championship of secondary school mathematics, and is held
each July in a host country somewhere in the world. A modern IMO involves
more than 100 countries, representing over 90% of the world’s population.
The competition was founded in 1959. Each participating country
may send up to six team members, who must be under 20 years of age
and not have entered university.
The UK Deputy Leader was Dominic Yeo of the University
of Oxford, and our Observer C was Jill Parker, formerly
of the University of Bath.
Here is the UK IMO team of 2015.
| Joe Benton | St Paul’s School, Barnes, London |
| Lawrence Hollom | Churcher’s College, Petersfield, Hampshire |
| Sam Kittle | Simon Langton Boys’ Grammar School, Canterbury, Kent |
| Warren Li | Eton College, Windsor |
| Neel Nanda | Latymer School, Edmonton, London |
| Harvey Yau | Ysgol Dyffryn Taf, Carmarthenshire, Wales |
The reserves were Liam Hughes of Robert Smyth Academy
and Harry Metrebian of Winchester College.
Here are the results obtained by the UK students this year.
| Name | P1 | P2 | P3 | P4 | P5 | P6 | Σ | award |
|---|
| Joe Benton | 7 | 2 | 1 | 7 | 1 | 1 | 19 | Silver |
| Lawrence Hollom | 7 | 1 | 0 | 1 | 1 | 0 | 10 | Honourable Mention |
| Sam Kittle | 7 | 2 | 0 | 7 | 3 | 0 | 19 | Silver |
| Warren Li | 7 | 7 | 1 | 7 | 3 | 0 | 25 | Silver |
| Neel Nanda | 7 | 1 | 0 | 7 | 2 | 0 | 17 | Bronze |
| Harvey Yau | 7 | 2 | 1 | 7 | 2 | 0 | 19 | Silver |
There are three problems to address on each of two consecutive days.
Each exam lasts 4 hours 30 minutes. The cut-offs were
14 for bronze, 19 for silver and 26 for gold. The current IMO
marks format became stable in 1981. This is the lowest gold cut,
and the equal lowest silver cut, since then. This is
evidence of the exceptional difficulty of this IMO, perhaps
because of the technical complexity of the medium problems, numbers 2 and 5.
There were 104 teams participating at IMO 2015.
Hearty congratulations to
the USA for finishing ranked 1st, the first time that they have achieved this
since 1994. However, this is the 15th time that they have achieved a top three
result in that period, so this is an event which has been waiting to happen.
It is very hard to beat a modern Chinese team in a fair fight, and the USA
joins only the Republic of Korea and Russia in achieving this.
Here are a few of the leading scores
(the nations gathering at least 80 points).
1 USA (185), 2 China (181), 3 Korea (161), 4 DPR Korea (156),
5 Vietnam (151), 6 Australia (148), 7 Iran (145),
8 Russia (141), 9 Canada (140), 10 Singapore (139),
11 Ukraine (135), 12 Thailand (134),
13 Romania (132), 14 France (120),
15 Croatia (119), 16 Peru (118),
17 Poland (117), 18 Taiwan (115), 19 Mexico (114),
20 Hungary, Turkey (113),
22 Brazil, Japan, United Kingdom (109),
25 Kazakhstan (105), 26 Armenia (104), 27 Germany (102),
28 Hong Kong (101), 29 Bulgaria, Indonesia, Italy, Serbia (100),
33 Bangladesh, Slovakia (97),
35 Macao (88), 36 Philippines (87), 37 India (86),
38 Moldova (85), 39 Belarus (84),
40 Israel (83), 41 Saudi Arabia (81), 42 Georgia (80)
Anglophone and Commonwealth interest in other scores might include
49 New Zealand (72),
55 South Africa (68),
57 Malaysia (66),
63 Cyprus (58),
70 Sri Lanka (51),
77 Ireland (37),
82 Trinidad and Tobago (26),
85 Pakistan (25),
88 Nigeria (22).
The inexperienced teams of Botswana, Ghana, Tanzania and Uganda
also participated, and as one would expect, did not score heavily.
Uganda were only one mark short of getting an honourable mention.
Here are the unusual prizewinners for 2015.
The first country to have its rank higher than its score was Algeria.
This very creditable performance included a silver medal, and left them only
8 marks behind South Africa. Thus South Africa’s position as the traditional champion of Africa may be under threat in the next few years.
It has been a very good year for monarchies,
with Australia leading the way in an astonishing 6th place,
with Canada in 9th and Thailand in 12th. Australia’s result
is impressive, especially given their performance when training with
the UK at our pre-IMO camp in Malaysia. The teams tied for the
Mathematical Ashes, and seemed well-matched. However, Australia had
a great IMO.
Luxembourg managed to retain the
Grand Duchy title, and will keep their firm grip
unless Finland or Lithuania revisits its constitutional
heritage, or Baden, Mecklenburg-Strelitz or Holstein-Oldenburg
breaks away from the Federal Republic of Germany.
Romania was the top member state of the European Union, one spot ahead
of France which is the leading country which uses the euro (behind
two countries which put Queen Elizabeth on their money:
Australia and Canada).
France is to be congratulated on finishing ranked above the UK for the
time since 2002.
Syria achieved its first silver medal, and Montenegro its first bronze medal.
Trinidad and Tobago obtained only its second ever silver medal. My apologies
if I have overlooked other singular achievements.
The Papers
Contestants have 4 hours 30 minutes to sit each paper. The three
problems on each paper are each marked out of 7. It is intended that
the three problems should be in increasing order of difficulty on each day.
Day 1
We say that a finite set 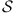 of points in the plane is
balanced if, for any two different points A and B in
of points in the plane is
balanced if, for any two different points A and B in
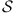 , there is a point C in
, there is a point C in 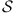 such that
AC = BC. We say that
such that
AC = BC. We say that 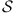 is centre-free if for any
three different points A, B and C in
is centre-free if for any
three different points A, B and C in 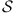 , there is no point P in
, there is no point P in 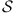 such that PA = PB = PC.
such that PA = PB = PC.
- Show that for all integers n ≥ 3, there exists a balanced set consisting of n points.
- Determine all integers n ≥ 3 for which there exists a balanced centre-free set
consisting of n points.
Determine all triples (a, b, c) of positive integers such that each of
the numbers
ab − c, bc − a, ca − b
is a power of 2.
(A power of 2 is an integer of the form 2n, where n is a non-negative integer.)
Let ABC be an acute triangle with AB > AC. Let Γ be its
circumcircle, H its orthocentre, and F the foot of the altitude
from A. Let M be the midpoint of BC. Let Q be the point on
Γ such that ∠HQA = 90°, and let K be the point on
Γ such that ∠HKQ = 90°. Assume that the points A, B, C, K and Q are all different, and lie on Γ in this order.
Prove that the circumcircles of triangles KQH and FKM are tangent to each other.
Day 2
Triangle ABC has circumcircle Ω and
circumcentre O. A circle Γ with centre A intersects the segment BC at
points D and E, such that B, D, E and C are all different and lie on line BC in this order. Let F and G be the points of intersection of Γ and Ω, such that A, F, B, C and G lie on Ω in this order.
Let K be the second point of intersection of the circumcircle of triangle BDF and the segment AB. Let L be the second point of intersection of the circumcircle of triangle CGE and the segment CA.
Suppose that the lines FK and
GL are different and intersect at the point X. Prove that X lies on the line AO.
Let ℝ be the set of real numbers. Determine all functions f : ℝ → ℝ satisfying the equation
f(x + f(x + y)) + f(xy) = x + f(x + y) + yf(x)
for all real numbers x and y.
The sequence a1, a2, … of integers satisfies the
following conditions:
- 1 ≤ aj ≤ 2015 for all j ≥ 1;
- k + ak ≠ ℓ + aℓ for all 1 ≤ k < ℓ.
Prove that there exist two positive integers b and N such that
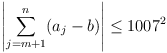
for all integers m and n satisfying n > m ≥ N.
These questions were proposed to the IMO by
(1) the Netherlands (Merlijn Staps),
(2) Serbia (Dusan Djukic),
(3) Ukraine (Danylo Khilko and Mykhailo Plotnikov),
(4) Greece (Vaggelis Psychas and Silouanos Brazitikos),
(5) Albania (Dorlir Ahmeti)
and (6) Australia (Ivan Guo and Ross Atkins).
Forthcoming International Events
This is a summary of the events which are relevant for the UK.
Of course there are many other competitions going on in other
parts of the world.
The next few IMOs will be held in Hong Kong 2016,
Brazil 2017,
Romania 2018 and the United Kingdom 2019. Forthcoming editions of
the European Girls’ Mathematical Olympiad will be in
Romania in 2016 and Switzerland in 2017.
The Balkan Mathematical Olympiad will be held in Albania in 2016,
and the Romanian Master of Mathematics will be in late February 2016.
Diary
This diary is a partly frivolous summary of my personal experience at the
IMO, and
is rarely fair, balanced or accurate. Bits of it are. Dominic Yeo’s report
as deputy leader contains far more information about the activities of
the students, and of course there are students’ reports too. The team leader
does not see the the students very much at the IMO, being busy with other
things. Jill Parker plays a huge role on the students’ side, but again our
paths hardly cross at the the IMO.
I thank the Thai organization for putting on an excellent IMO. It
was exceptionally well staffed, and that certainly helped
to make things run very smoothly. The people who were
my window on the Thai organization were the always helpful Rachaya Srisurichan
from the Secretariat and jury chair Soontorn Oraintara who showed
unfailing courtesy, excellent judgement and great energy.
However, I am acutely aware that I never even had the chance to meet
most of the huge army of organizers who worked harmoniously
to create this truly excellent IMO, and it is their triumph that
the rest of us enjoyed. Thank you so much!
I also want to draw attention to the unsung heroes of the IMO,
the Ethics Committee. Rafael Sanchez of Venezuela, Paul Vaderlind
of Sweden, Roberto Dvornicich of Italy and
Dávid Kunszenti-Kovács of Norway who do a huge
amount of work behind the scenes to make sure that
everything is fair and above board.
Finally, note that this is the last year of support for the
IMO by Google. They generously donated a million euros
to support us for five years back in 2011. This was an exceptionally
timely gift, since the world was still in shock from the economic
disaster of 2008, and we were not at all sure that IMO host nations
could be found. The Google donation got us through an exceptionally
difficult period. Tip your hat.
A Plea to other team leaders
Now that I have become chair of the IMO Advisory Board, I have become
the recipient of
gifts from generous people who come from cultures where this is
deemed appropriate. I am grateful for these items of course, but there
is a problem. My suitcase is finite. Large, fragile and heavy gifts are
not very convenient.
Let me emphasize, there is absolutely no need to give me a present.
A smile and a handshake are more than enough. However, if you feel that
you really must make a gift, then please change your mind. Finally,
if you can’t change your mind, then please make the gift small and light.
Thanks! I am sure that similar remarks apply to the gifts which leaders and
students exchange with one another.
June 30th
A taxi containing Jill Parker,
our pastoral specialist, calls in
at my home to pick up me and my
suitcase. I have failed to pack my phone charger. Since no-one really wants to
speak to me anyway, this is not a problem. I will manage to nurse the phone
for quite a while, only using it as nature intended, as an alarm clock.
Our rail journey was not quite on time, and we missed our bus connection
at Reading Station. We catch the next service, and the motorway traffic
conditions are not helpful. Tension is just starting to build when we break
free, and arrive at Heathrow Terminal 5 fashionably but not worryingly late.
Dominic Yeo has
everything in hand, and forges ahead with the team while Jill and I check
in.
After the usual process rituals with immigration and security,
we meet up to find that
Dominic is keen on Wagamama dining. I cannot resist a Japanese
Ramen. Time is passing, and there is concern that we might not arrive at the gate on time.
There is much frantic shopping en route to the shuttle, but happily we
all arrive at the departure gate in good order, and in time to enjoy some
queueing.
We depart soon after 9pm, and each adopt our coping strategies. I watch
a film called Kingsman: The Secret Service (2014)
which is a parody of the spy genre. It
panders to under-achievers everywhere (possibly its target audience) by railing
against the social injustice of it all, and exploring the comedic possibilities
of violent death. It did pass the time on an
intercontinental flight, and so it is fit for purpose, if not for
small children.
July 1st
Flying East means that days and nights are compressed, so the schedule
is dinner, sleep, breakfast, land. However, the journey ends in the afternoon
by local time, so it doesn’t quite work. We are in Kuala Lumpur airport,
because we are having a pre-IMO camp in Malaysia with our Australian
friends.
We will be staying at Nexus International School in Putrajaya, between
Kuala Lumpur and its airport. The school has kindly offered to send a
minibus. The driver is in the arrivals hall, and we are escorted
through thick tropical air to the bus.
Now there is a problem, because we are 9 strong, we all have suitcases, and
the Tardis feature on the bus is broken.
We use a form of three-dimensional tetris to box me in behind a wall
of baggage,
and set off for the school. My dodgy knee is cramped, folded and
is causing me acute pain, but fortunately no-one
else cares.
Putrajaya is Malaysia’s answer to Canberra. It
is the administrative centre of government, and we chose to go there because of what it does not have: pollution, noise and big city life.
The school turns out to be very well suited to our needs. It has
vigorous air-conditioning, lots of space for lounging around and
being a teenager (if you are), and excellent showers which are
cleaned continuously throughout the hours of daylight.
It is the holy month of Ramadan, so some care must be taken to plan for
meals. The school has helpfully made arrangements for an evening adventure.
July 2nd
The Australians are due in the afternoon. In the morning
we take a boat trip on the artificial Putrajaya Lake. Attempts to follow this
with a visit to mosques were foiled by the presence of worshippers.
How could we be expected to foresee that?
We adjourned to a Chinese Restaurant next to some botanical gardens,
and let the passage of time
do its gentle work on our jet lag.
We return to the school and soon we are joined by most of the Australians including
their dazzling team leader, Angelo di Pasquale.
We go out to dinner, and as planned, we are intercepted there by
Australian Maths Trust royalty, Mike Clapper and Jo Cockwill.
July 3rd
The teams go to work on their first practice exam,
but before they finish I leave for the airport and fly to IMO Chiang Mai. At the airport I see
a backpacker being given a hard time by
an immigration official.
The Thais welcome short term visitors, but understandably have little time for impecunious travellers who seek to
take up semi-permanent residence.
I am met by the efficient IMO organization, and am transported to the hotel. The traffic near the airport is jammed, but after that things loosen up. The city is bustling and thoroughly Asian. The leaders’ hotel is a Holiday Inn,
and very luxurious. I have a room on floor 14 which overlooks the river Ping.
People are fishing in the river which
is a very good sign. The advantage of a swish hotel is the personal
comfort. The disadvantage is that hotel bars are very expensive, and
this is not convenient in the evenings since leaders from less developed
countries will shy away from prices which they must regard as absurd.
Strangely, the IMO shortlist is not yet available, and we will have to
wait until tomorrow morning. This seems very odd, since some leaders have
travelled a day early in order to start their work as soon as possible.
Future IMO hosts please note: if you are not issuing the shortlist
to early arrivers, then tell them in advance, and then they probably
won’t come.
July 4th
This is the normal arrival day for leaders, but
I am busy at the annual IMO Advisory Board meeting. We have no
formal offers to host IMOs beyond 2019, but even so there is a lot of
business. In particular, we have a plan to make the selection of
the medal cut-offs in a more sensible way. This will involve displaying
the various options as bar charts, with the actual marks removed.
This will, we hope, lead to more rational decision making, as
leaders will not be sure of the consequences of the chosen cuts
for their own students. There are all sorts of other matters to discuss
too.
July 5th
Work on the shortlist.
This is not very entertaining
for the reader, so I will tell you about my adventures with
journalism instead. Before leaving the UK, there had been a nice piece on
the IMO and EGMO (European Girls’ Mathematical Olympiad) in The
Guardian, written by Sally Weale, and the paper was keen to do
follow-up stories. Their stringer in Thailand is Oliver Holmes,
and he will visit us in Chiang Mai on the day of the
closing ceremony.
There are all sorts of possibilities for a story, as well as covering the
results of IMO 2015. He seems very interested in the possibility of
getting people to disagree with one another about the wisdom of
having a separate maths competition for girls. I can see that
this sort of dispute will go down very well with The Guardian’s
target demographic. I suggest various people to put the pros and cons,
and he eventually talks with Kirsten Rosenkilde of Denmark and
Jana Madjarova of Sweden. That story has yet to surface, so we await
a quiet news day in the UK.
July 6th
It is time to choose the papers. The jury has
voted
heavily in favour of the protocol I proposed in 2013. This protocol
has the advantage that each of the main subject areas gets represented
among problems 1, 2, 4 and 5, and every problem used is deemed the best
of its type. The case against the protocol is that the jury loves to
choose G1, the easiest geometry problem, and unless the jury can
exercise more self-control than usual, there will never be a
medium level geometry problem in the papers. My view is that the jury
needs to get a grip on itself, and sometimes not select G1. That way we can
sometimes have some medium geometry.
We choose the paper using a smooth application of the protocol,
and the jury chair Soontorn did a great job.
July 7th
In the morning the English
language version of the paper was burnished and eventually approved
after lunch.
The rest of the day was spent creating versions in
other languages. In the evening I read that our Mathematical Ashes contest
against the Australians has been a draw. Given that the Australians
will go on to perform brilliantly at this IMO, the UK
can count itself lucky
to retain the Ashes. Fortunately for us, Australia peaked a little too late.
July 8th
Student arrival day. The jury has worked speedily,
and you might think that they have nothing to do. However, after approving
the different language versions, the
fourth law of thermodynamics kicks into action. This is better
known as Parkinson’s law: work expands to fill the time available
for its completion. The phase where problem captains and the jury
negotiate the mark schemes normally lasts a couple of hours. However,
there is no need for such unwarranted efficiency, and the process
goes on all day. I take an hour off for a nap in the afternoon, but when
I return the same leaders are saying the same things. You know who you are.
July 9th
Today we have the opening ceremony, and we have
the honour that HRH Crown Princess Sirindhorn will be presiding. Our Thai hosts
take Royal matters very seriously, and so we do too. European Royalty is
a very relaxed business these days, and protocol is established
with a very light touch. I remember being told before meeting
the British Princess Royal “if you wish to use the traditional form
of address, this is how you do it”.
This is not the case with Thai protocol, which is prescriptive,
theatrical and serious.
The students have to be in
place in the ceremonial hall very early, and the leaders are
lucky that they only have to arrive an
hour before the Royal Party. We go through airport-style weapons
scans, and also have our
temperatures taken (so as not to risk the health of the Princess).
I get to sit at the front because as Advisory Board
chair, I am to make a speech.
As I sit there, a Thai official in a Top Gun style white uniform
walks towards me. He leans forward, smiles, and says “you don’t remember me do you?”
and then walks away. It turns out that he is the master of ceremonies, and speaks
excellent English.
My speech has been through a few iterations, following exchanges
with the royal household. I have submitted it, and was told I would
get a version to use in the ceremony. I have a spare copy in my inside pocket
just in case. I need not have worried, for a lady-in-waiting approaches
me with a beautifully bound folder which contains the speech. She also gives
me a tutorial in bowing. It must be from the waist, and slow. I am to bow twice
on the way in, and twice on the way back from the podium. I decide to regard
it as conjugation, so I am to bow, walk, bow, speak, bow inverse, walk inverse and
finally bow inverse again.
The speech goes as well as I could hope. It is not really MLK’s “I have a dream”
nor Kennedy’s “ask not what your country can do for you”, but when I look up
in mid speech, the Princess is smiling broadly. She must have to sit through a lot
of formalities, so I admire her professionalism.
Part of the speech consists of administering the IMO oath, exhorting participants
to play fair. The oath is an important reminder of the IMO spirit. We
have an Ethics Committee
translating and scrutinizing scripts between IMOs. To quote another
US President, “trust but verify”.
After my speech I introspect, trying to work out where I have met the master of ceremonies
before, and I realise that he was a student at the University of Bath
a long time ago. After the ceremony is over, I go over and find out the details.
He is Natee Tongsiri, and in time of yore he was a postgraduate student in
my university when I was the Conference Director of
Groups St Andrews in Bath 1997, and he played the important role
of minibus driver. It is wonderful to see him again after all this time.
In the afternoon the jury spends hours discussing self-denying ordinances.
The jury is sovereign and supreme, but the jury is naughty, and
the jury feels guilty about being naughty. The jury
sometimes breaks its own rules. So, the IMO AB has a cunning plan to
make the jury obey its own rules. How? More rules of course. Anyway,
it is worth a try, and perhaps at the final jury meeting the medals really
will be given to at most half the contestants, and the ratio of
gold:silver:bronze really will be an excellent approximation to 1:2:3.
July 10th
First Contest Day. This begins innocently enough. The leaders take a
bus to the students’ hotel where they are sitting the paper. This device simplifies the
Question and Answer session during the first half hour of the exam. Students are allowed
to ask questions of clarification, and the jury entertains itself by splitting into
a helpful faction and a hard-as-nails group. At least, that is the traditional entertainment.
This year there are lots of noisy observers and poor acoustics, so it is very hard to
hear what is going on.
After the Q&A we are taken by bus to an elephant park. Just as I settle in to see elephants
paint, miss penalty kicks and drag logs, news comes through of a possible IMO irregularity. The Russian
leader Nazar Agakhanov has had a phone call telling him that some deputies have been
given copies of the day 2 paper (on day 1). Since the deputies mix with the students, this
is an irregularity. I consult with Advisory Board Secretary Gregor Dolinar, and contact the jury
chair Soontorn Oraintara. Information about what has happened is sketchy, and the phone signal
at the elephant camp is poor. We consult the elected members of the IMO AB as best we can, and
quickly decide that we have to take emergency action. IMO AB people and the Problem Selection Committee are
put on a bus, and return to the jury hotel, leaving everyone else to engage in elephant related activities.
We also bundle Joseph Myers onto the bus, because he sits in the jury and makes exhaustive notes of everything
that happens. We will need him to reconstruct the jury’s discussions.
We decide that, in case the jury wants to reset the Day 2 paper, we have to facilitate this.
We therefore construct various candidate replacement Day 2 papers, using both the opinions of the
Problem Selection Committee, and the previously established opinions of the jury
concerning the merits of the problems. Finally we realise that there are two good choices,
and we have those ready.
When the jury returns, we have a meeting before dinner. The evidence about the scale of
the irregularity is not conclusive, so the jury sensibly decides to be very careful,
and chooses to reset the paper. Time is very short, because after dinner the new paper
will have to be translated, approved and printed. The jury chooses the paper with little fuss.
The jury, the co-ordinators and the Thai organizers worked very hard that evening, and
by the start of Day 2, the situation was recovered.
In the end it turned out that a sequence of apparently minor mistakes and suboptimal decisions
compounded to cause the problem. The people involved are loyal and hardworking friends
of the IMO, so let us draw a veil of discretion over precisely what happened. Of course those mistakes
will not happen again, we will make sure of that.
July 11th
The day of the second exam. I detect a little
nervousness, given the amazing speed at which the selection and translation
was made. Have we forgotten something? However, everything runs very smoothly.
We have a joint IMO AB and jury meeting, and remember IMO friends
who have died during the previous year with short speeches and a silence.
There is a brief opportunity to meet deputies, but mine is half way up
a mountain as usual. However, I am able to snatch a chat with Jill and
she reassures me that the team members are OK.
The jury has a mid-morning lunch at the students’ hotel, and then piles back
to the leaders’ hotel to agree the marking schemes for the new Day 2 problems.
We need to do this in a hurry because the students will finish the paper soon.
Therefore the leaders are not present to greet the students as they leave the
second exam. It is often annoying when this happens, but this time there
was a very good reason for the arrangement.
I finally meet the UK students in the late afternoon, and they are not really
jubilant. It has been a demanding paper, and many scores will be low,
but that is
little comfort.
July 12th
The first day of co-ordination begins with
a morning off. Our Thai hosts have arranged a generous schedule, so there
is plenty of time to work on the scripts. Dominic and I have divided the
responsibilities. I will handle the three problems with geometric content
(including Problem 1), and Dominic will handle the others. As it
happens, that means that Dominic will fight for scraps whereas I will harvest
marks.
I quickly dispose of Problem 3 in the afternoon. We ask for
100101 and get the marks easily enough. This question is a tribute to the
nine-point circle, and as always happens with well-known
configurations, there will be grief concerning “obvious” properties
of the diagram. In this case it was Hungarian unhappiness.
July 13th
We are supposed to co-ordinate four questions today, but in fact we
finish everything. Co-ordination is very straightforward because the
hosts have prepared very well and there are more tables than usual,
so much less queueing is needed.
Luckily we begin first thing in the morning, and are among the first
to co-ordinate Problem 6. This gives Dominic an excellent opportunity
to persuade the co-ordinators to vary their marking scheme, because
Joe has made non-trivial progress on the problem, and his ideas can be
completed to a full solution. The existing mark scheme would have
him score 0, but by deploying the natural justice argument, he gets
1 mark. This only works because we are on first, and the co-ordinators
have not had the chance to build the “this is the way we have treated
all other scripts” into an unvarying mantra.
The other co-ordinations are less fraught, and we are pleased that
we do not feel the victim of an injustice at any table. The easiest
session was for Problem 1, when the co-ordinators started to congratulate
us on our excellent scripts even before we sat down. That is the
civilized way
to bag 42 marks. Problem 1 is a play on the Sylvester-Gallai theorem, the
result that states that if you have n points in the plane, and every line
through two of these points contains a third, then all the points
must be on a line. The balanced condition replaces
a line through two points by their
perpendicular bisector. In fact parts of Problem 1 turn out to be a known,
but the jury decided several years ago that with easy problems,
the requirement for complete originality is not realistic. People who
demand complete originality should take up problem composition as a hobby.
In general, we have not done as well as usual on the medium problem, and
only Warren has scored full marks in the category on Day 1, and no-one
on Day 2. By scheduling an extra meeting, we complete co-ordination a day
early.
In the evening it turns out that Joseph Myers, the UKMT volunteer who
is here as a co-ordinator is free, so we jump in one of the
surprisingly unprecarious 3-wheeled taxis, with a plan to join
the students for dinner. The driver gives every sign of knowing
where the restaurant is to be found, but this turns out to be false. He lets us out
in the general vicinity of the correct restaurant, close to a nearby junction.
There is a sleazy joint filled with bar girls
(or similar). I am not experienced in such situations,
so I send in Joseph to use his urbane charm and easy manner to extract
information. This fails for some reason.
I take charge, and decide to use racism to solve the problem.
We walk around the junction until I see a European face. I then
use the subtle “excuse me, do you speak any English” line, and we
are directed straight to the restaurant.
We have a happy time with the students, Jill and Dominic.
I ask for extra heat in my soup, and end up in tears. It was excellent.
July 14th
The UK leaders are now on vacation, but co-ordination continues
in the morning for some countries. These are the countries
with difficult scripts to handle, together with those countries
with vexatiously argumentative leaders. In the afternoon
there is an excursion, but I elect for the indoor horizontal option.
We have the final jury meeting in the evening. There is one appeal
to the jury concerning marking practice, but it is rejected.
I have been told of the death of another former IMO team leader,
and am moments away from making an announcement and calling for a silence.
I check the exact pronunciation
of his surname with that country’s current team leader, only to be
informed that the person concerned has not
died. I am delighted to have been misinformed. Welcome back.
The new bar chart method of displaying the results works extremely
well, and it is completely clear where the bronze and silver cuts should
be. The jury is not being naughty! The IMO AB recommended reforms
are working. There is room to debate where the gold cut should be.
Remember that the jury does not know the cut it is making; it only
knows that there are two rational choices and they are one mark apart.
I assume that the jury will err on the side of generosity, but no.
The jury is now intoxicated with its own virtue, and is determined
to implement the ratio rules as best it can. There is a close vote,
because there is room for honest disagreement here, and finally
the jury chooses.
After this, the actual cuts are revealed; 14, 19 and 26, and
suddenly we see the consequences of our actions.
UK student
Warren Li is one mark short of a gold medal. This is painful,
but at least no marks were left in the co-ordination
room, and he got every mark that he earned. Three British
students Joe Benton, Sam Kittle and Harvey Yau have
snuck silver medals by scoring 19. Neel Nanda has a very safe bronze
on 17, and finally Lawrence Hollom has an Honourable Mention
for solving Problem 1 perfectly.
Alex Song, a Canadian student, has the only perfect score, and this
takes him to the top of the IMO hall of fame. The Americans have edged
out the Chinese, and it seems quite possible that Po-Shen Loh, the US leader,
will explode with joy. The UK has four silver medals for the second year
running, and 11 in the past three years.
July 15th
In the early afternoon the closing ceremony begins,
of which there are a very large number of photographs on the internet.
The video for the forthcoming Hong Kong IMO of 2016 is particularly clever,
and the whole thing is done with class and efficiency.
Afterwards we walk to the site of a superb buffet banquet. The Guardian journalist
is around, and I hope that he is picking up some good stories. I am taken to sit
at the front with the dignitaries. There is entertainment on stage, and
after a while a procession of Thai dancers enters the hall from the back.
They are carrying lights, and the lead dancer is being carried on a platform.
She appears to be modelled on Audrey Hepburn, but is covered in a layer
of metallic sheen in the manner of Shirley Eaton in the Bond film Goldfinger.
She presents me with a jasmine bracelet, but I decide to read nothing personal
into this.
This front table has the advantage that people bring you
food, and so you don’t have to forage. Eventually most of the key figures from
the Thai local organization drift away, and I return to join the UK students.
The music is a touch loud for my tastes, especially since I have been
down the front near the speakers.
The UK IMO gift this year consists of IMO logo stickers. These circular objects
were designed so that people could use them to decorate their luggage, and thereby
recognize suitcases on airport carousels more easily. These are now leaking into
the hands of students, and unsurprisingly they start to use them in unexpected
ways, mainly as fashion accessories, decorating their clothes and faces
with IMO symbols. This could become a habit.
I share an open back red Thai taxi with Australians leaders.
Angelo di Pasquale
entertains us with some background information about Problem 6.
The authors were Ivan Guo and Ross Atkins. It is a problem inspired
by the mathematics of juggling. Imagine that you have just one hand, and
can throw balls in the air so that their flight time is an integer
number of seconds. You have a supply of balls, and you must arrange that
you never have two balls landing in your hand at the same moment.
Now Problem 6 looks completely natural, and b stands for the final number of
balls in play.
July 16th
In the morning Dominic and I board a bus to Chiang Mai airport at 06:30. Traffic is very
light, and now it is much more obvious how close we have been staying to the airport. For logistical reason
too tedious to explain, I am bringing an extra suitcase home. AirAsia have an economic model which may be
familiar to readers from other parts of the world. The flights themselves are very cheap, but unless you
do everything correctly in advance and on-line, there are punitive charges waiting for you at the airport.
This policy
works in conjunction with a web site of such a poor (or malicious) design that the user is tempted to
give up and pay the airport fine, or possibly to walk to the destination instead.
Various people have done battle with this site on behalf of UKMT, and and in fact Jill Parker has heroically
checked in almost all the luggage except mine. The problem here is the extra suitcase, and we can’t work out
how to do that. The only solution is to pay the airport charge (ouch). However, this charge underscores
how well she has done in checking in the rest, since we saved the best part of £1000 that way.
The UK party flies to Kuala Lumpur where we must pass about eight hours.
We have asked my undergraduate friend and KL resident, Dave Bobker, to
find a civilized way to pass the time. Using his high level administrative
skills, he has passed the job to Mrs Bobker, the excellent Maria.
Maria has hatched a plan to have a long slow meal in the Hilton Hotel,
handily situated next to KL railway station.
At the airport the UK party follows instructions, and takes the fast train
into KL, keeping the Bobkers informed of our schedule. The train is impressive
and modern, and affords interesting views of the state of Malaysian urban
development. In summary, it is mixed.
Dave and Maria meet us at the station and escort us to the hotel
and the banquet. One of the UK students is not feeling too bright
and we are
in a hotel, so we get him a bedroom to rest.
At length we make our way back to the airport. The rest of the party check in easily
enough, but although I know for certain that Bev Detoeuf in the UKMT office
has booked me to take two suitcases, British Airways are in denial.
They have to poke their software with sticks and hit their terminals with rocks
but eventually they discover that UKMT has indeed booked two suitcases for
me. I am glad to get through that, but am alarmed when my boarding card
causes the machine to flash red at the gate. I assume that there must be
another problem with the luggage, but instead it turns out that BA have
decided to upgrade me to Business Class, presumably as an apology
for all the trouble about the suitcase. I find it hard to look the
other UKMT passengers in the eye.
July 17th
We arrive safely at T5 Heathrow at about 05:00.
The correct number of parents turn up. There is some emoting but
of course I will have no part in this. It is far too early in the morning.
The IMO excursion is over for another year.
Acknowledgements
The UK Mathematics Trust is an astonishing organization, bringing together so many volunteers
and a small professional core to focus their energies on maths competitions
and more generally, mathematics enrichment. Our collective effort is, I am sure,
a significant part of the success story which is secondary school mathematics
for able students in the UK. This is not to be complacent, because there are
always opportunities do more things and to do things better, but I thank
everyone for what we already accomplish every year.
These days UKMT’s work even stretches into the Primary School sector.
Hundreds of thousands of lives are touched by our wonderful maths challenges and team competitions,
and I thank everyone involved for their marvellous work.
On a personal note, I thank Dominic Yeo,
Jill Parker and Joseph Myers for their help during the year and while
we were on the road. The teams which UKMT sends
abroad to represent the country (and the associated reserves) continue
to conduct themselves in an exemplary fashion. We must redouble our
efforts to draw in more girls.
I thank Oxford Asset Management for their continuing generous
sponsorship of the UK IMO team, and the other donors, both individual
and corporate,
who give so generously to UKMT. Why not join in?
http://www.ukmt.org.uk/about-us/
G.C.Smith@bath.ac.uk @GeoffBath
Return to IMO Register home page
Contact: Joseph Myers
(imo-register@imo-register.org.uk)
Online HTML version last updated:
5 January 2016
![]() of points in the plane is
balanced if, for any two different points A and B in
of points in the plane is
balanced if, for any two different points A and B in
![]() , there is a point C in
, there is a point C in ![]() such that
AC = BC. We say that
such that
AC = BC. We say that ![]() is centre-free if for any
three different points A, B and C in
is centre-free if for any
three different points A, B and C in ![]() , there is no point P in
, there is no point P in ![]() such that PA = PB = PC.
such that PA = PB = PC.