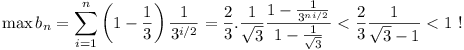International Mathematical Olympiad 1970
Bryan Thwaites (Leader) and Margaret Hayman (Deputy Leader), the
British Team
This International Olympiad was the twelfth of the series and, as
in recent years, invitations to participate had been received by
certain countries of Western Europe. This year, Hungary was the host
country, and all the arrangements were made at governmental level by
the Hungarian Ministry of Cultural Affairs.
The organisation followed the pattern of previous years. Each
participating country provided a “leader”, who was a
member of the “jury” which was the sole arbiter of all
things academic—the choice of questions, their marking and
moderating, and the decision on prize-winners. A “deputy
leader” looked after each country’s team of eight
students, none of whom was yet at University.
For the British mathematicians, there are acute difficulties. All
the Democratic Socialist countries of East Europe attach great
importance to the Olympiad, and regard it as an operation from which
much prestige can be gained. The same seems hardly less true for the
Western European countries, with the one exception of Britain. It is
not easy to see why the British Government is so reluctant to
recognise the evident advantages to be derived from groups of young
people of the very highest intelligence cohabitating and competing
together over a period of 12 days or so.
Organisationally, the lack of official Government support creates
considerable problems for the two leaders and the schoolboy
participants. As Government acceptance is dependent on an assurance
that adequate funds have been made available by private industry to
the Committee for Mathematical Awards of the Mathematical Association,
the official programme may not be made available to the teams
beforehand, which makes the timetabling of the party largely a matter
of guesswork. Thus, this year, the leaders were obliged to
extrapolate from previous years to arrange the return journey, only to
find on arrival in Hungary that the British delegation, to the
amazement and disbelief of the other national delegations, would miss
the final ceremonies and prizegiving.
The participation of a British delegation this year was in doubt
until the very last moment, owing to the necessity of raising the
cost—about £1000—from purely private sources, at
very short notice.
To us, it is clear that, in the eyes of at least the communist
countries, the British entry is not a serious one. Thus, when it
comes to purely mathematical aspects, the questions submitted
beforehand from Britain go unregarded; the British attitude to
mathematics is barely heeded; and the final six questions are biased
towards the kind of mathematics a typical clever Russian 17-year-old
will be doing, and away from what a British sixth-former is likely to
experience.
To be more precise, one might look at the six questions set this
year, which follow this Report. If the Oxbridge scholarship
examinations were to be used as a yardstick, one might opine that only
one question—number 2—is of a kind which might be found as
a scholarship question. Question 1 is too “trad” as a
straight triangle rider; question 3 (a nice question) does not seem to
lie within the typical orbit of sixth-form inequalities; question 4
deals with a kind of number theory which we seem to by-pass; question
5 is another inequality of (dare we say?) a rather uninspiring kind;
and question 6 involves essentially an application of induction which
would be unfamiliar to most English classrooms.
This year 14 countries took part, of which five were from Western
Europe. From the total number of questions submitted earlier in the
summer by each leader, it is the host country’s prerogative to
choose some 12 problems to serve as a basis for discussion by the
jury. To those accustomed to the difficulties of setting, for
example, A-level questions, it will appear a formidable task for a
committee of 14, speaking and thinking in 14 different languages with
interpreters working in four languages, to arrive at six sensible,
well-phrased, questions. Indeed, this process took two long
days’ work.
As it turned out this year, the final stages of compiling each
question seemed best done with an English draft text, and the English
leader was able to make a substantial contribution at this stage, when
it became clear that some other leaders would have preferred much more
complicated and pseudo-rigorous formulations of the same
questions.
When it came, finally, to approve the set of six perfected
questions, the British leader abstained from voting. He felt that too
much stress was being laid on the formulation of inequalities, and too
little on the solution of any kind of equation or mathematical model;
and that the overall balance in the mathematics was unreasonably, and
unnecessarily, to the disadvantage of the British boys.
Against this was set the view that within that sphere of
mathematics for which equalities can be formulated, the inequality is
of greater interest and of more fundamental significance than the
equality; that “solving equations” was not a very
profitable intellectual exercise; that models outside the geometric,
or those involving rates-of-change, were not deemed to be
“within the syllabus”; and, finally, that if the boys were
of the highest calibre, then the type of problem was irrelevant. (On
these various points, it would be interesting to form some kind of
British view for the benefit of future delegations).
The abstention caused a minor international incident, for it was at
once construed as a veto. The jury then launched itself with
never-flagging zeal into a seminar on the theory of democracy, during
which the British leader expounded the principles of making up the
rules of the game as you go along, with by no means a total lack of
success. The abstention prevailed.
Thereafter, definitive versions of each question were agreed in the
four “official” languages, each leader translated them
into his own language—and then settled down to typing out 10
copies.
Another interesting comparison of national mathematical viewpoints
arose when the number of marks for each question came to be decided.
Eventually they were agreed as follows: 5, 7, 8, 6, 6, 8, totalling
40. The candidates were not told of these relative weights. No
marking scheme was agreed within each question.
While all the preliminaries were going on (in a not very attractive
holiday resort some 100 miles west of Budapest), the teams were
settling elsewhere.
That the entire British team and deputy leader reached Keszthely on
Lake Balaton—after a 6.15 a.m. start, and the chaos of the
railway station in Budapest, with an interpreter who didn’t know
which train they were trying to catch—was most surprising. In
Keszthely, they stayed in a boarding school for catering students
where the accommodation was pleasant, and food was adequate but
dull.
The first two days were left free, and the students made friends
with members of other teams and swam in the lake, with the exception
of Russia, East Germany and Hungary whose teams had long training
sessions. After the papers were taken, the leaders at last broke out
of their rigid isolation and were allowed to mix with the deputy
leaders and the rest of the teams.
Once the scripts had been completed, furious activity broke forth.
Each leader and deputy leader first marked their team’s papers,
though without putting the marks on the scripts. Then a very
complicated system of “co-ordination” took place, whereby
each question would be read by its own small specialist team of young
Hungarian mathematicians, whose job it was to ensure that the marking
of that question over all 14 teams was fair.
The attitude to detailed explanation varied considerably between
the coordinators, some being interested merely in the argument, and
others insisting that even the most obvious statements were proved in
detail. In the case of disagreement, the leader of the delegation
from the country which set the question was the final arbiter. It
seems that full marks were given for complete solutions, even if not
by the best method, but marks were lost for incomplete argument even
when the steps seemed trivial.
The jury then met and, after a relatively brief discussion about
methods of marking and coordination—and of how far a marking
scheme, and priorities of proof, should be decided by the jury before
marking is started—settled to the very protracted task of
deciding the marks for 1st, 2nd, and 3rd prizes.
Opinion divided between making the prizes reflect good work, and
making them span at least one pupil from each country. Finally, after
three hours of discussion, the decision was in accord with the second,
rather than the first, principle:
1st prize 40–37 marks, 7 pupils;
2nd prize 36–30 marks, 11 pupils;
3rd prize 29–19 marks, 40 pupils.
Later, there was an equally long session on the relative merits of
individual solutions for special prizes. A brief solution is not in
itself sufficient, but one which can be generalised immediately, even
if this has not been carried out, was deemed worthy of merit. How far
a very good mathematical generalisation which depends on special
knowledge, rather than elementary methods, was deserving of a prize
was also discussed at some length.
Finally the following were agreed—an East German for question
3, a Hungarian for a generalisation of question 4, and another
Hungarian, a Czech and a German for brief solutions of the questions,
which are directly capable of some generalisation, even though this
was not carried out, and two Hungarian students who found the equality
in question 6.
Considering that G.B. is the only country which has no special
training—even Sweden had a three-day training session before
leaving for the competition—the British team did very well. If,
however, we are to compete on equal terms then we must consider a
method whereby the student can have some experience of the sort of
questions that will be asked, and practice at answering such
questions.
While the leader and deputy leader were mathematically engaged, the
boys had more swimming, games and conversation, and the whole group
had a pleasant reception given one evening by the local education
department, and a boat trip on the Lake, which included a wine-tasting
for the grown-ups.
In spite of having to leave early, the boys enjoyed their
experience and gained a great deal, particularly from meetings with
pupils from other countries. Only with the Mongolian team did they
fail to communicate.
The following table lists the score by countries:
| Total | | Total |
|---|
| Austria | 104 | Hungary | 233 |
| Bulgaria | 145 | Mongolia | 78 |
| Czechoslovakia | 145 | Poland | 105 |
| France | 141 | Romania | 208 |
| German Dem. Rep. | 221 | Sweden | 110 |
| Great Britain | 180 | U.S.S.R. | 221 |
| Holland | 87 | Yugoslavia | 209 |
The numbers in each Class were I, 7 (British 1, German 1, Russians 2,
Hungarians 3); II, 11; III, 40 (British 6). Bernard Silverman, City
of London School, scored 39 out of 40.
The British team scored as follows by questions:
| Question | |
|---|
| Entrant | 1 | 2 | 3 | 4 | 5 | 6 | Total |
|---|
| 1 | 5 | 7 | 8 | 5 | 6 | 8 | 39 |
| 2 | 5 | 4 | 0 | 6 | 6 | 0 | 21 |
| 3 | 5 | 6 | 1 | 4 | 0 | 0 | 16 |
| 4 | 5 | 7 | 0 | 2 | 6 | 0 | 20 |
| 5 | 5 | 7 | 0 | 5 | 6 | 0 | 23 |
| 6 | 1 | 7 | 0 | 5 | 0 | 8 | 21 |
| 7 | 5 | 7 | 0 | 6 | 1 | 2 | 21 |
| 8 | 0 | 7 | 6 | 4 | 1 | 1 | 19 |
| | | | | | | 180 |
The average team score was 48.8 per cent. The British team average
was 56.25 per cent.
Questions and Solutions
First Day (4 hours)
-
M is a point on the side AB of
the triangle ABC. r1,
r2, r are the radii of the
incircles of triangles AMC, BMC,
ABC; and ρ1,
ρ2, ρ are the radii of the
ecircles of the same triangles corresponding to the sides
AM, BM, AB. Prove
that
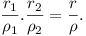
(Poland, 5 marks)
Solution:erratum
One may first recall (or derive fairly simply) the standard
triangle formulae
r = 4R
cos ½A
cos ½B
cos ½C
and ρ = 4R sin ½A
sin ½B
cos ½C for ecircle opposite
A.
whence
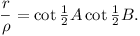
So denote CMA by D.
Then
Notes:
(i) A “transformation geometry” solution would be
welcomed.
(ii) The interesting generalisation that
∏(ri/ρi) = r/ρ.
-
Let a, b and n be
integers greater than unity; and let the numbers a,
b be the bases of two number systems.
The numbers An, Bn have the
same representation
xnxn−1xn−2.....x1x0
in the bases a, b, where
xn ≠ 0 and
xn−1 ≠0. The numbers obtained by
deleting the first digit xn are
An−1, Bn−1. Prove
that a > b if and only if
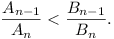
(Romania, 7 marks)
Solution:
Let 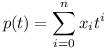 and
and 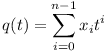
so that An/An−1 = p(a)/q(a).
It suffices to prove that p(t)/q(t) is
monotonically increasing.
Which follows from ![p(t)/q(t) = 1 + (x_n t^n / q(t)) = 1 + x_n [ \sum_{i=0}^{n-1} (x_i / t^{n-i}) ]^{-1}.](1970-sol2eq2.png)
-
The real numbers a0, a1, .....,
an, ..... satisfy
1 = a0 ≤ a1 ≤ ..... ≤ an ≤
..... (1)
The numbers b1, ....., bn,
..... are then defined by
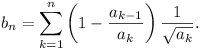
(i) Prove that
0 ≤ bn < 2 for all
n.
(ii) Also, given c such that
0 ≤ c < 2, prove that
there exist numbers a0, a1,
..... satisfying the property (1) and for which
bn > c for infinitely
many n.
(Sweden, 8 marks)
Solution:
(i) A simple calculus proof follows, though it would not be
admitted by most other European countries.
First, bn ≥ 0 is trivial from the
definitions.
Second:
![b_n = \sum_{k=1}^n a_k^{-3/2}(a_k - a_{k-1}) < \int_1^{a_k} x^{-3/2} dx = -2[a_k^{-1/2} - 1] < 2.](1970-sol3eq0.png)
(ii) Choose x > 0.
c < x(x + 1) < 2,
and put ak = x−2k.
Then 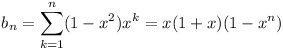 which increases
monotonically to the limit x(1 + x) as
n → ∞.
which increases
monotonically to the limit x(1 + x) as
n → ∞.
Note:
This limit can clearly be made to lie as close to 2 as
required. What therefore is wrong with the following argument
produced by one of the candidates?
The maximum value of bn will be obtained by
ensuring that the ai’s give the maximum
value of (bi −bi−1) for each
bi−1. Thus, regarding
ai−1 as fixed,
![(d(b_i - b_{i-1}) / da_i( = (d / da_i) [ a_i^{-1/2} - a_{i-1} a_i^{-3/2} ] = -½a_i^{-3/2} + (3/2)a_{i-1}a_i^{-5/2}](1970-sol3eq2.png)
so that (bi − bi−1) is
maximised for ai = 3ai−1.
Thus, with a0 = 1,
ai = 3i, and 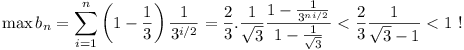
Second Day (4 hours)
-
Find the set of all positive integers n with the
following property:
“Given the set { n, n + 1,
n + 2, n + 3, n + 4,
n + 5 }, it is possible to partition it
into two sets such that the product of the members of one set
equals the product of the members of the other set.”
(Czechoslovakia, 6 marks)
Solution:
If a prime p divides any of the six numbers, it
must divide at least two of them for the property to hold. Thus
p ≤ 5. Furthermore 5 divides only
n, n + 5. Thus the only
prime division of n + 1,
n + 2, n + 3,
n + 4, are 2 and 3, but of these 4
numbers two are odd, and so must be powers of 3, which is
impossible since their difference is 2. Hence the answer is the
empty set.
-
In the tetrahedron ABCD, DB is
perpendicular to DC, and the foot of the
perpendicular from D to the plane
ABC is the orthocentre of the triangle
ABC.
Prove that (AB + BC + CA)2 ≤
6(DA2 + DB2 + DC2). For what
tetrahedra does the equality hold?
(Bulgaria, 6 marks)
Solution:
First it may be proved by a variety of methods that all three angles
at D are right-angles.
Second, 6(DA2 + DB2 + DC2)
− (AB + BC + CA)2
= 3(AB2 + BC2 + CA2) −
(AB + BC + CA)2
= (AB − BC)2 + (BC − CA)2
+ (CA − AB)2
≥ 0.
The equality holds only if
AB = BC = CA.
-
100 coplanar points are given, no three of which are
collinear.
Prove that, of all the triangles which can be drawn with these
points as vertices, not more than 70 per cent are
acute-angled.
(Russia, 8 marks)
Solution:
For a quadrilateral, at least one angle ≥ 90°, so at least
1 out of the 4C3 = 4 triangles is
obtuse.
With additional, fifth, point, there are 4C2
extra triangles (making 10 in all) and there are
4C3 = 4 extra quadrilaterals which give
at least ½ . 4 = 2 extra obtuse
triangles, to make at least 3 obtuse triangles all told.
Given 100 points, every five points therefore contribute at
least 3/10 = 30 per cent obtuse triangles, and so in all
not more than 70 per cent of triangles is acute-angled.
Report reproduced from Science Teacher volume 14 number 1 (October
1970) pages 1–6.
I have been unable to locate the copyright holder of Science
Teacher; if you believe you own the copyright, please let me
know.
Note an erratum notice by Geoff Smith to the
solution to problem 1.
Return to IMO Register home page
Contact: Joseph Myers
(imo-register@imo-register.org.uk)
Online HTML version last updated:
5 January 2016
![]()
![]()
![]()
![]() and
and 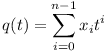
![p(t)/q(t) = 1 + (x_n t^n / q(t)) = 1 + x_n [ \sum_{i=0}^{n-1} (x_i / t^{n-i}) ]^{-1}.](1970-sol2eq2.png)
![]()
![]()
![]() which increases
monotonically to the limit x(1 + x) as
n → ∞.
which increases
monotonically to the limit x(1 + x) as
n → ∞.![]()